3.1
円錐や半円などの重心に関してはテキストに記述してあるものを参照してください。
ここで特に解説はしません。
(a)2つの直線と半円弧に分けて考えます。$$x_{G} = \frac{\int_{}^{}{x}dL}{L}$$また、半円弧の重心は$$y_{G} = \frac{2r}{π}$$
であるから
となります。
(b)4つの直線に分けて考えます。
3.2
$$x_{G} = \frac{\int_{}^{}{x}dA}{A}$$である。
(a)15cm×10cmと6cm×6cmの長方形に分けて考えると
(b)左側の半径4cmの半円、台形、右側の半径2cmの半円、左側の半径2cmの円、右側の半径1cmの円に分けて考えると
(c)半径10cmの扇型と半径5cmの扇型に分けて考えると
3.3
$$x_{G} = \frac{\int_{}^{}{x}dV}{V}$$である。
(a)3つの円柱に分けて考えると
(b)高さ0cmで半径5cmの円が高さ5cmの地点で半径3cmになっているため、下図のようにして高さを求める

比を考えてxを求めると$$5 : 3 = 5 + x : x$$$$x = 7.5[cm]$$となる
半径5cmの円を底面とした高さ(5+7.5)cmの円錐Aと、半径3cmの円を底面とした高さ7.5cmの円錐Bに分けて考える
円錐A , Bそれぞれの体積は
よって物体の体積は$$V = V_{A} - V_{B} = \frac{245}{3}\pi$$
高さhの円錐の重心位置はh/4であるから、円錐A , Bの重心位置はそれぞれ
よって求める重心位置は
$$x_{G} = 2.1[cm]~~y_{G} = 0$$
(c)
3.4
Aから重心までの距離をxとするとA,Bまわりのモーメントのつりあいより$$W_{A}l = Mg(l-x)$$$$xMg = W_{B}l$$これらより$$M = \frac{W_{A} + W_{B}}{g} , x = \frac{W_{B}l}{W_{A} + W_{B}}$$
3.5
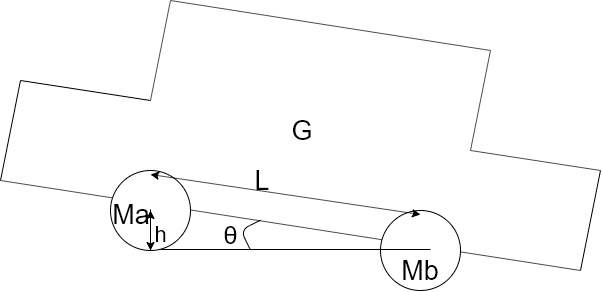
前輪を基準として重心の位置を求める。
まず、前輪を持ち上げていないときの前輪中心のモーメントのつり合いより$$(M_{A}g + M_{B}g)x = M_{B}L$$$$x = \frac{M_{B}L}{(M_{A} + M_{B})}$$
次に傾斜角をθとするとsinθ = h/L , tanθ = h/√L^2-h^2であるから
前輪を持ち上げたときの前輪中心のモーメントのつり合いより
yについて整理して$$y = \frac{M_{b}L}{M_{a}+M_{b}} - \frac{M_{B}L}{M_{A}+M_{B}}$$総重量は一定であるからM_A + M_B = M_a + M_bより$$y = \frac{(M_{b} - M_{B})L\sqrt{L^2 - h^2}}{h(M_{A} + M_{B})}$$

3.6
パップスギュルダンの定理より「重心の移動距離 × 面積 = 体積」であるから重心の位置をdとすると
$$\frac{4}{3}πr^3 = \frac{πr^2}{2}*2πd$$より$$d = \frac{4r}{3π}$$
3.7
これもパップスギュルダンの定理より$$V = 5^{2}π*60π = 14.8*10^3[cm^{3}]$$表面積は「表面積 = 重心の移動距離 + 円周」より
3.8
中立のすわりであるから半球と直円錐の接地面が重心となる。よって重心周りのモーメントのつり合いより$$\frac{2}{3}πr^{3}\frac{3}{8}r = \frac{r^{2}πh}{3}*\frac{h}{4}$$整理して$$h = \sqrt{3}r$$
3.9
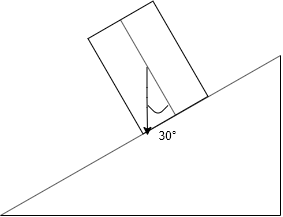
これは重心から垂直におろした線が円柱の底面内にあれば倒れないので最大値になるにはその線が底面の端に来るところになります。よって図より円柱の高さhは$$h = 10*2*\sqrt{3} = 34.6[cm]$$
間違い、質問などありましたらコメントよろしくお願いいたします。

