1辺の長さaの正方形の面積は、もちろん\(a^2\)ですが、正三角形の面積公式は知っていますか
中学や高校の試験で登場するため、正三角形の面積公式は覚えておいて損はありません
そして、さらに知りたい方のためにも、正五角形…正二十四角形と他の多角形の面積公式についても解説していきます
正多角形の面積公式一覧
1辺の長さaの多角形の公式一覧です
| 図形 | 面積 |
| 正三角形 | \( \frac{\sqrt{3}}{4}a \) |
| 正方形 | \( a^2 \) |
| 正五角形 | \( \frac{\sqrt{25+10\sqrt{5}}}{4}a^2 \) |
| 正六角形 | \( \frac{3\sqrt{3}}{2}a^2 \) |
| 正八角形 | \( (2\sqrt{2} + 2)a^2 \) |
| 正十角形 | \( \frac{5\sqrt{5+2\sqrt{5}}}{2}a^2 \) |
| 正十二角形 | \( (3\sqrt{3} + 6)a^2 \) |
| 正二十四角形 | \( (6\sqrt{6} + 6\sqrt{3} + 6\sqrt{2} + 12)a^2 \) |
公式の導出方法
正多角形の面積導出には、sinで表す三角形の面積公式\(\frac{1}{2}\sin{\theta}ab\)を使用します
この公式の導出についてはこちらの記事で解説していますので、興味のある方は是非ご覧ください
では、辺の数が少ないものから順番にやっていきます
正三角形
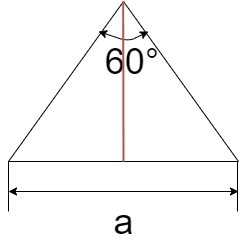
頂点から垂線を下ろして、三平方の定理より高さhは
$$h = \sqrt{a^2 - (\frac{a}{2})^2} = \frac{\sqrt{3}}{2}a$$
よって面積Sは
$$S = \frac{a\times \frac{\sqrt{3}}{2}a}{2} = \frac{\sqrt{3}}{4}a^2$$
また、高校数学の知識で解くと
$$S = \frac{1}{2}a^2 \sin{60^\circ} = \frac{\sqrt{3}}{4}a^2$$
と、簡単に求められます
正方形
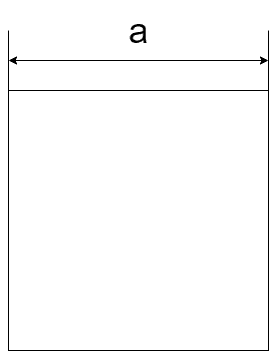
これは説明不要ですね\( S = a\times a = a^2 \)
正五角形
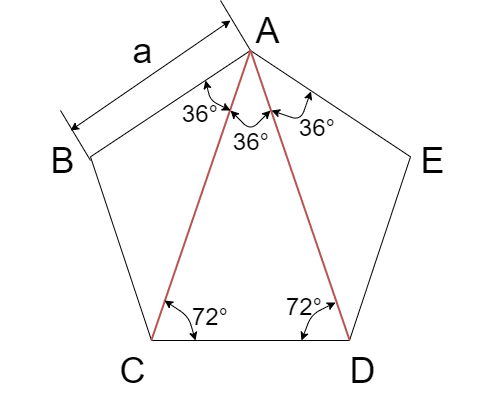
上の図のような五角形ABCDEについて考える
五角形の内角は\( \frac{180 + 360}{5} = 108^\circ \)であるから、AからCとDに対角線を引くと、上図のような角度が得られる
次に、三角形ACDに注目する。\(\angle C\)の二等分線とADの接点をFとする

\( \triangle AFC~,~\triangle CDF \)は二等辺三角形であるから、CF = a , AF = aとなる
また、\( \triangle AFC \sim \triangle CDF \)であるから
AD = xとすると、比の関係より
$$\begin{align*}
a:x = x-a:a\\
x^2 - ax = a^2\\
x^2 - ax = a^2\\
x^2 - ax -a^2 = 0
\end{align*}$$
二次方程式の解の公式より
$$\begin{align*}
x
&= \frac{a\pm \sqrt{a^2 + 4a^2}}{2}\\
&= \frac{1 \pm \sqrt{5}}{2}a
\end{align*}$$
x > 0より
$$x = \frac{1 + \sqrt{5}}{2}a$$
これで正五角形の対角線の長さが求められました
これを使って、面積を求めていきます
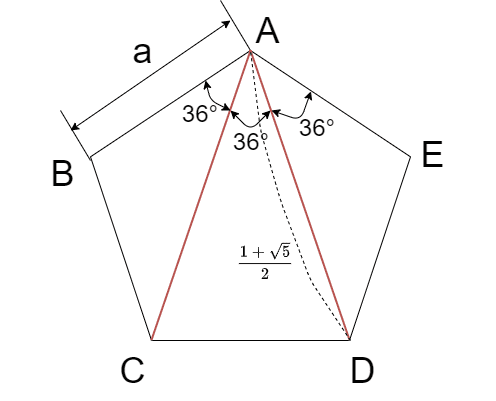
正五角形の面積Sは\( \triangle{ABC}~,~ \triangle{ACD} ~,~\triangle{AED} \)の和であるから
$$\begin{align*}
S
&= 2 \cdot \frac{1}{2}a \cdot (\frac{1+\sqrt{5}}{2}a) \cdot \sin{36^\circ} + \frac{1}{2}\cdot (\frac{1+\sqrt{5}}{2}a)^2 \cdot \sin{36^\circ}\\
&= \frac{1+\sqrt{5}}{2}a^2 \sin{36^\circ} + \frac{(1+\sqrt{5})^2}{8}a^2 \sin{36^\circ}\\
&= \frac{a^2}{8}\sin{36^\circ}\{ 4(1+\sqrt{5}) + (1+\sqrt{5})^2 \}\\
&= \frac{a^2}{8} \sin{36^\circ} (10+6 \sqrt{5}) \cdots ①
\end{align*}$$
ここで、\(\sin{36^\circ}\)について考えます
θ = 36°とすると、5θ = 180°であるから、これを変形して
$$3\theta = 180^\circ - 2\theta$$
両辺のsinをとると
$$\sin{3\theta} = \sin{180^\circ} - 2\theta = 2\theta$$
二倍角と三倍角の公式より
$$3\sin{\theta} - 4\sin ^3 \theta = 2\sin{\theta}\cos{theta}$$
sin36° ≠ 0より
$$3 - 4\sin ^2 \theta = 2\cos{\theta}$$
\(\sin ^2 \theta + \cos ^2 \theta = 1\)より
$$4\cos ^2 \theta - 2\cos{\theta} - 1 = 0$$
二次方程式の解の公式より
$$\cos{\theta} = \frac{1 \pm \sqrt{5}}{4}$$
\( \cos{36^\circ} > 0\)より
$$\cos{\theta} = \frac{1 + \sqrt{5}}{4}$$
よって
$$\begin{align*}
\sin{36^\circ}
&= \sqrt{1 - \cos ^2 \theta}\\
&= \sqrt{1 - \frac{6 + 2\sqrt{5}}{16}}\\
&= \sqrt{\frac{10 - 2\sqrt{5}}{16}}
\end{align*}$$
sin36° > 0より
$$\sin{36^\circ} = \frac{\sqrt{10 - 2\sqrt{5}}}{4}$$
これを①に代入して
$$\begin{align*}
S
&= \frac{a^2}{8} \cdot \frac{\sqrt{10 - 2\sqrt{5}}}{4} \cdot (10 + 6\sqrt{5})\\
&= \frac{a^2 \sqrt{(10 - 2\sqrt{5})(5+3\sqrt{5})^2}}{16}\\
&= \frac{\sqrt{(10 - 2\sqrt{5})(70+30\sqrt{5})}}{16}a^2\\
&= \frac{\sqrt{400+160\sqrt{5}}}{16}\\
&= \frac{25 + 10\sqrt{5}}{4}a^2
\end{align*}$$
となり、面積が求められました
正六角形

正六角形は、対角線を引くと、長さaの正三角形6つで構成されていることが分かります
正三角形の面積は\(\frac{\sqrt{3}}{4}a^2\)であるから、正六角形の面積は
$$S = 6 \cdot \frac{\sqrt{3}}{4}a^2 = \frac{3\sqrt{3}}{2}a^2$$
と、求められます
正八角形

1辺の長さがaの正八角形は、以下のように正方形を考えます

正方形の中に正八角形が入っている状態です
正方形の面積から4隅の青い三角形の面積を引けば、正八角形の面積が求められます
正八角形の内角は\( \frac{360+180\times 4}{8} = 135^\circ\)です
なので、青い部分の三角形は、底角が45°の直角二等辺三角形になります

底辺の長さがaなので、他の二辺は\( \frac{a}{\sqrt{2}} \)になります
よって、三角形の面積は
$$\frac{(\frac{a}{\sqrt{2}})^2}{2} = \frac{a^2}{4}$$
正方形の面積は
$$(a+2\cdot \frac{a}{\sqrt{2}})^2 = (3+2\sqrt{2})a^2$$
よって、正八角形の面積Sは
$$S = (3+2\sqrt{2})a^2 - 4 \cdot \frac{a^2}{4} = (2+2\sqrt{2})a^2$$
正十角形
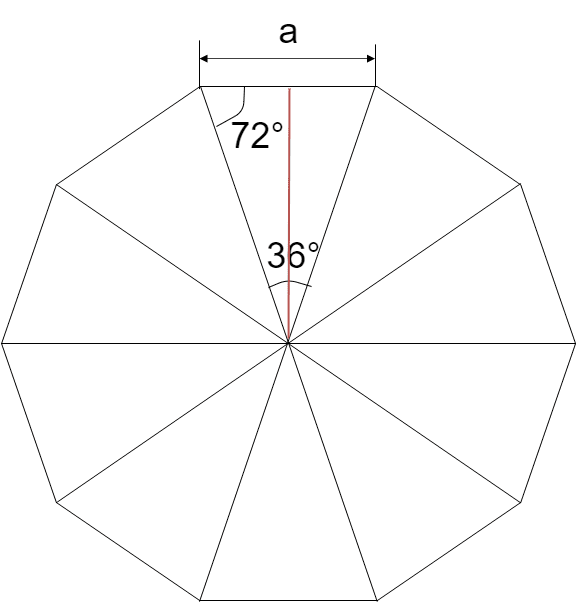
正十角形の内角は、\( \frac{360+180\times 6}{10} = 144^\circ \)であるから
1辺の長さがaの正十角形は、中心から辺に垂線を下すと、上図のような角度が得られる
次に、下図のような三角形について考える
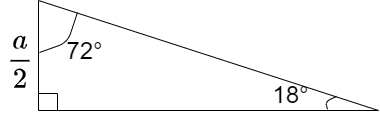
斜辺の長さをxとすると、\( x = \frac{a}{2\sin{18^\circ}} \)と求められる
ここで、sin18°について考えます
18° = θとすると、5θ = 90°であるから、これを変形して
$$3\theta = 90^\circ - 2\theta$$
両辺のsinをとると
$$\sin{3\theta} = \sin(90^\circ - 2\theta) =\cos{2\theta}$$
二倍角と三倍角の公式より
$$3\sin{\theta} - 4\sin ^3 \theta = 1 - 2\sin ^2 \theta$$
$$(\sin{\theta} -1)(4\sin ^2 \theta + 2\sin{\theta} -1) = 0$$
sin18° ≠ 1より
$$4\sin ^2 \theta + 2\sin{\theta} -1 = 0$$
二次方程式の解の公式より
$$\sin{\theta} = \frac{-1 \pm \sqrt{5}}{4}$$
sin18° > 0より
$$\sin{\theta} = \frac{-1 + \sqrt{5}}{4}$$
なので、三角形の斜辺の長さxは
$$\begin{align*}
x
&= \frac{a}{2\sin{18^\circ}}\\
&= \frac{a}{\frac{-1+\sqrt{5}}{2}}\\
&= \frac{2a}{\sqrt{5}-1}\\
&= \frac{a(\sqrt{5} + 1)}{2}
\end{align*}$$
と、求められます
正十角形を十等分した三角形の一つの面積\(S_{small}\)は
$$S_{small} = \frac{1}{2} x^2 \cdot \sin{36^\circ}$$
で、求められる
sin36は、正五角形の面積導出のところで\(\sin{36^\circ} = \frac{\sqrt{10 - 2\sqrt{5}}}{4}\)と求めたので、これを代入して
$$\begin{align*}
S_{small}
&= \frac{1}{2} x^2 \cdot \sin{36^\circ}\\
&= \frac{1}{2} \{\frac{a(\sqrt{5} + 1)}{2}\}^2 \cdot \frac{\sqrt{10 - 2\sqrt{5}}}{4}\\
&= \frac{1}{2} \cdot \frac{a^2(\sqrt{3} + \sqrt{5})}{2} \cdot \frac{\sqrt{10 - 2\sqrt{5}}}{4}\\
&= \frac{a^2 (3+\sqrt{5})\sqrt{10 - 2\sqrt{5}}}{16}\\
&= \frac{a^2 \sqrt{9+6\sqrt{5} + 5 + 10 -2\sqrt{5}}}{16}\\
&= \frac{a^2\sqrt{24+4\sqrt{5}}}{16}\\
&= \frac{a^2 \sqrt{5+2\sqrt{5}}}{4}
\end{align*}$$
と、求められます
これ10個の和が、正十角形の面積Sとなるから
$$S = 10S_{small} = \frac{5\sqrt{5+2\sqrt{5}}}{2}a^2$$
と、求められました
正十二角形
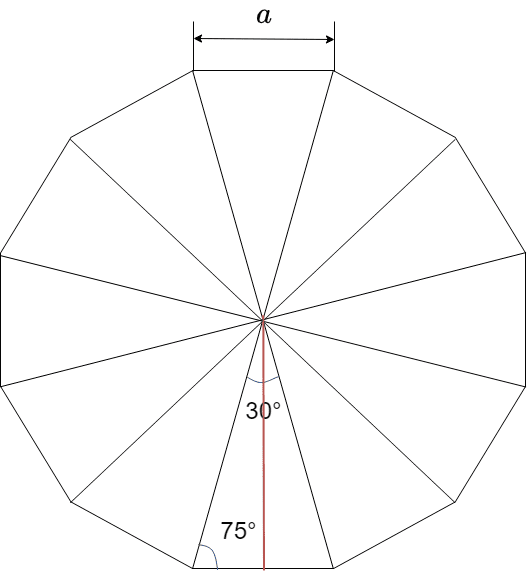
正十二角形の内角は、\( \frac{360+180\times 8}{12} = 150^\circ \)であるから
1辺の長さがaの正十二角形は、中心から辺に垂線を下すと、上図のような角度が得られる
次に、下図のような三角形について考える
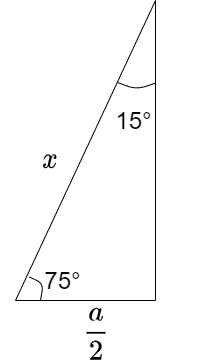
斜辺の長さxは
$$x = \frac{a}{2 \cos{75^\circ}}$$
で、求められる
cos75°は、加法定理より
$$\begin{align*}
\cos{75^\circ}
&= \cos{(30^\circ + 45^\circ)}\\
&= \cos{30^\circ}\cos{45^\circ} - \sin{30^\circ}\sin{45^\circ}\\
&= \frac{\sqrt{3}}{2}\cdot \frac{1}{\sqrt{2}} - \frac{1}{2}\cdot \frac{1}{\sqrt{2}}\\
&= \frac{\sqrt{3}-1}{2\sqrt{2}}\\
&= \frac{\sqrt{6} - \sqrt{2}}{4}
\end{align*}$$
となるから
$$\begin{align*}
x
&= \frac{a}{2 \cos{75^\circ}} \\
&= \frac{a}{\frac{\sqrt{6} - \sqrt{2}}{2}}\\
&= \frac{a(\sqrt{6} + \sqrt{2})}{2}
\end{align*}$$
正十二角形を十二等分した三角形一つの面積\(S_{small}\)は
$$\begin{align*}
S_{small}
&= \frac{1}{2} x^2 \cdot \sin{30^\circ}\\
&= \frac{1}{2} \cdot \{\frac{a(\sqrt{6} + \sqrt{2})}{2}\}^2 \cdot \frac{1}{2}\\
&= \frac{2+\sqrt{3}}{4}a^2
\end{align*}$$
これ12個の和が、正十二角形の面積Sであるから
$$S = 12S_{small} = (3\sqrt{3} + 6)a^2$$
と、求められました
正二十四角形
正二十四角形の内角は\( \frac{360+180\times 20}{24} = 165^\circ \)であるから
これまでと同様に考えて、以下の三角形のxを求めていく

$$x = \frac{a}{2\sin{7.5}}$$
である
ここで、cos15°は加法定理より
$$\begin{align*}
\cos{15^\circ}
&=\cos{(60^\circ - 45^\circ)}\\
&= \cos{60^\circ}\cos{45^\circ} + \sin{60^\circ}\sin{45^\circ}\\
&= \frac{1}{2}\cdot \frac{\sqrt{2}}{2} + \frac{\sqrt{3}}{2} \cdot \frac{\sqrt{2}}{2}\\
&= \frac{\sqrt{6} + \sqrt{2}}{4}
\end{align*}$$
であるから、sin7.5は、半角の公式より
$$\begin{align*}
\sin{\frac{15}{2}}
&= \sqrt{\frac{1 - \cos{15^\circ}}{2}}\\
&= \sqrt{\frac{1- \frac{\sqrt{6} + \sqrt{2}}{4}}{2}}\\
&= \sqrt{\frac{4 - (\sqrt{6} + \sqrt{2})}{8}}\\
&= \frac{\sqrt{8-2(\sqrt{6} + \sqrt{2})}}{4}
\end{align*}$$
となるので、xは
$$\begin{align*}
x
&= \frac{a}{2\sin{7.5}}\\
&= \frac{2a}{\sqrt{8-2(\sqrt{6}+\sqrt{2})}}
\end{align*}$$
と、求められる
ここで、sin15° > 0であるから
\(\sin{15^\circ} = \sqrt{1 - \cos ^2 15^\circ} = \frac{\sqrt{6} - \sqrt{2}}{4}\)となる
正二十四角形を二十四等分した三角形一つの面積\(S_{small}\)は
$$\begin{align*}
S_{small}
&= \frac{1}{2} x^2 \cdot \sin{15^\circ}\\
&= \frac{1}{2} \frac{4a^2}{8-2(\sqrt{6}+\sqrt{2})} \cdot \frac{\sqrt{6} - \sqrt{2}}{4}\\
&= \frac{a^2}{4}\frac{\sqrt{6} - \sqrt{2}}{4-(\sqrt{6}+\sqrt{2})}\\
&= \frac{a^2}{4}\cdot \frac{(\sqrt{6}-\sqrt{2})(4+\sqrt{6}+\sqrt{2})}{8-4\sqrt{3}}\\
&= \frac{a^2}{4}\cdot \frac{(1+\sqrt{2}+\sqrt{6})}{2-\sqrt{3}}\\
&= \frac{a^2}{4}(2+\sqrt{2}+\sqrt{3}+\sqrt{6})
\end{align*}$$
となります
これ24個の和が、正二十四角形の面積Sであるから
$$S = 24S_{small} = (6\sqrt{6} + 6\sqrt{3} + 6\sqrt{2} + 12)a^2$$
と、求められました
まとめ
今回は、正多角形の面積公式の一覧と導出方法についてまとめてみました
定期試験などでは、正三角形、正方形くらいまでしか使わないと思いますが、探求心で他の多角形の導出も見てみると面白いと思います
最後までお読みいただきありがとうございました
