リンク機構の自由度の求め方を説明していきます
リンク機構や対偶についての説明は以下の記事をご覧ください
-
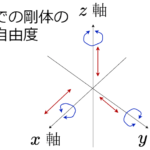
対偶の種類とそれぞれの自由度
続きを見る
-
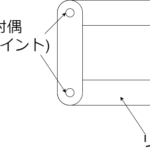
リンク機構についての簡単まとめ
続きを見る
グルーブラーの式
グルーブラーの式は、リンク機構の自由度を求めるための式です
この式さえ理解すれば、必要な数値を代入するだけでリンク機構の自由度は簡単に求められます
2次元でのグルーブラーの式は以下のようになります
$$\begin{align*}
&\Large{DOF = 3(L-J-1)+\displaystyle \sum_{i=1}^J f_i}\\
&\small{DOF:Degree of Freedom(自由度)}\\
&\small{L:リンクの数}\\
&\small{J:ジョイントの数}\\
&\small{f_i:各ジョイントの自由度}
\end{align*}$$
3次元でのグルーブラーの式は以下のようになります
$$\begin{align*}
&\Large{DOF = 6(L-J-1)+\displaystyle \sum_{i=1}^J f_i}\\
&\small{DOF:Degree of Freedom(自由度)}\\
&\small{L:リンクの数}\\
&\small{J:ジョイントの数}\\
&\small{f_i:各ジョイントの自由度}
\end{align*}$$
例題
【問題】
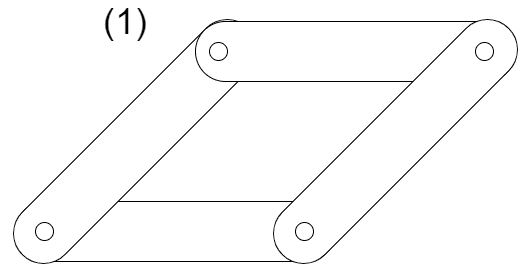
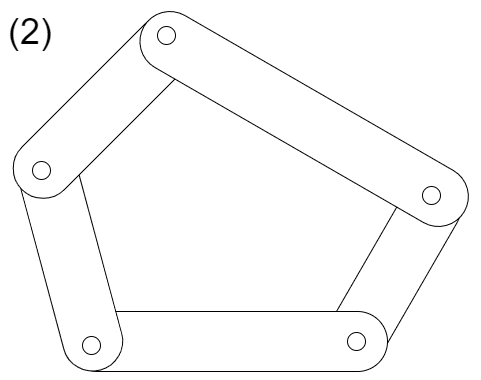
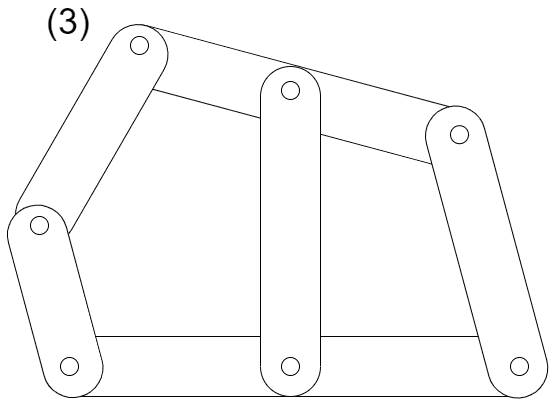
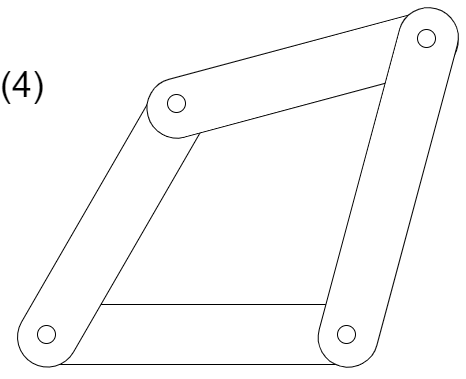
次のリンク機構(1)~(4)の全体の自由度を求めよ
ただし、(1)~(3)の全ての対偶は回転対偶とし、(4)の全ての対偶は球対偶であるとする
【解答】
(1)リンクの数は4つ、ジョイントの数は4つ、回転対偶の自由度は1であるから、それぞれの値を2次元でのグルーブラーの式に代入して
$$\begin{align*}
FOD &= 3(4-4-1)+1\times 4\\
&= -3 + 4\\
=1
\end{align*}$$
自由度1となります
(2)同様にリンクの数は5つ、ジョイントの数は5つ、回転対偶の自由度は1であるから、それぞれの値を2次元でのグルーブラーの式に代入して
$$\begin{align*}
FOD &= 3(5-5-1)+1\times 5\\
&= -3 + 5\\
=2
\end{align*}$$
自由度2となります
(3)リンクの数は6つ、ジョイントの数は7つ、回転対偶の自由度は1であるから、それぞれの値を2次元でのグルーブラーの式に代入して
$$\begin{align*}
FOD &= 3(6-7-1)+1\times 7\\
&= -6 + 7\\
=1
\end{align*}$$
自由度1となります
(4)対偶が球対偶となっているため、3次元で考える
リンクの数は4つ、ジョイントの数は4つ、球対偶の自由度は3であるから、それぞれの値を3次元でのグルーブラーの式に代入して
$$\begin{align*}
FOD &= 6(4-4-1)+3\times 4\\
&= -6 + 12\\
&=6
\end{align*}$$
自由度6となります
【参考】
https://www.slideshare.net/mechaholic/kutzbach-criteria-and-grublers-criteria
https://ja.wikipedia.org/wiki/%E3%83%AA%E3%83%B3%E3%82%AF%E6%A9%9F%E6%A7%8B