回転運動の角度などに使用するradという単位について簡単に解説します
弧度法とその単位rad
弧の長さで角度を表す単位の表し方を弧度法と呼びます
度数法の単位は[°]でしたが、弧度法の単位は[rad]になります
具体的には、半径\(r\)と等しい長さの弧をもつ扇形の中心角を1[rad]とします
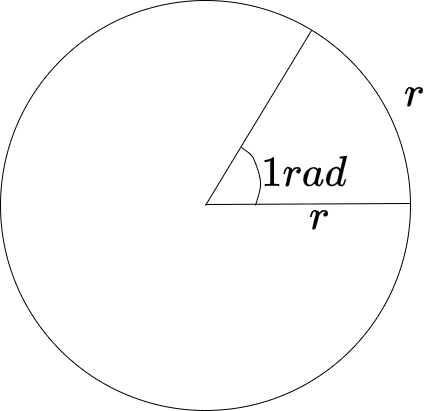
度数法との変換
半径を\(r\)とすると円周の長さは\(2\pi r\)ですので、弧度法で円の角度を表現すると
$$\frac{2\pi r}{r} = 2\pi[rad]$$
度数法では円の角度は360[°]であるから
$$\frac{2\pi r}{r} = 2\pi [rad] = 360[°]$$
よって
弧度法→度数法は
$$1[rad] = \frac{180}{\pi}[°]$$
度数法→弧度法は
$$1[°] = \frac{\pi}{180}[rad]$$
のようになります
例題
(1)\(\frac{\pi}{3}[rad]\)を度数法で表せ
(2)\(270[°]\)を弧度法で表せ
【解答】
(1)
\(1[rad] = \frac{180}{\pi}[°]\)より
$$\frac{\pi}{3} \times \frac{180}{\pi} = 60[°]$$
(2)
\(1[°] = \frac{\pi}{180}[rad]\)より
$$270[°] \times \frac{\pi}{180} = \frac{3}{2}\pi[rad]$$