機構学の対偶と自由度について簡単にまとめていきます
対偶
2つの機素(機械を構成する最小単位)が点、線、面で接して運動しているとき、接触部分の組み合わせのことを対偶(ジョイント)と呼びます
対偶には主に「点対偶」、「線対偶」、「面対偶」の3種類が存在しています
点対偶
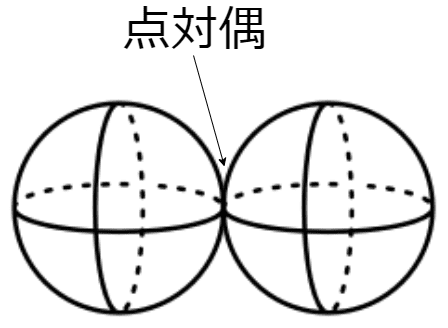
点対偶は機素が点で接触する対偶で、球が接触しているようなものを指します
玉軸受などが点対偶にあたります
線対偶
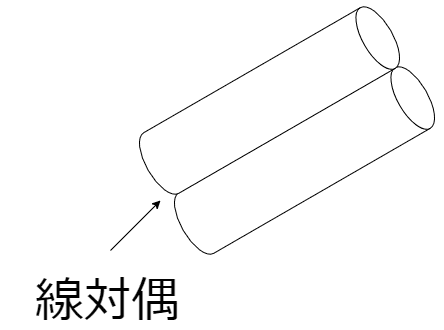
線対偶は機素が線で接触する対偶で、円柱が接触しているようなものを指します
ころ軸受などが線対偶にあたります
面対偶
面対偶は機素が面で接触する対偶で、平板が平面を移動する滑り運動するものを指します
面対偶は接触の種類によって「滑り対偶」、「回り対偶」「ねじ対偶」、「球面対偶」に細かく分けられます
滑り対偶

並進運動をするような対偶を滑り対偶と呼びます
ノギスなどが滑り対偶にあたります
進み対偶とも呼ばれます
回り対偶
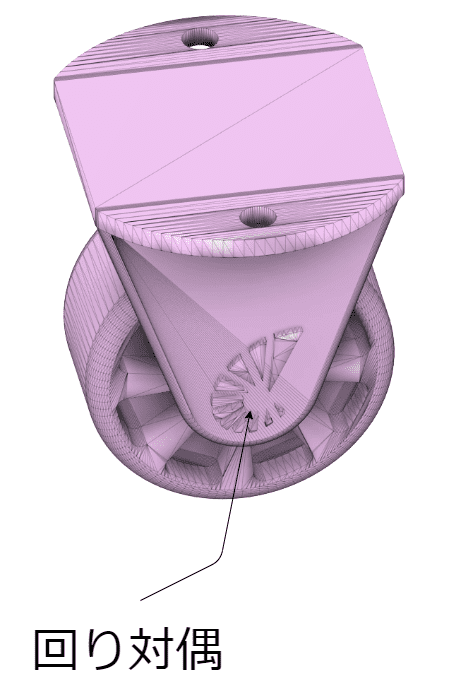
回転運動をするような対偶を回り対偶と呼びます
カートのタイヤのように、軸と軸受けの関係のようなものを指します
ねじ対偶

ねじによる組み合わせで回転運動と並進運動を同時に行うような対偶をねじ対偶と呼びます
ボルトとナットの組み合わせのようなものを指します
らせん対偶とも呼びます
球面対偶

球面の一部分を包んだような対偶を球面対偶と呼びます
ボールキャスターや球面滑り軸受などが球面対偶にあたります
自由度
自由度とは、物体を動かすことができる方向の数のことです
空間での剛体の自由度は、x,y,z軸方向の移動とx,y,z軸周りの回転で合計6つ存在しています

それぞれの対偶の自由度を見ていきます
点対偶の自由度
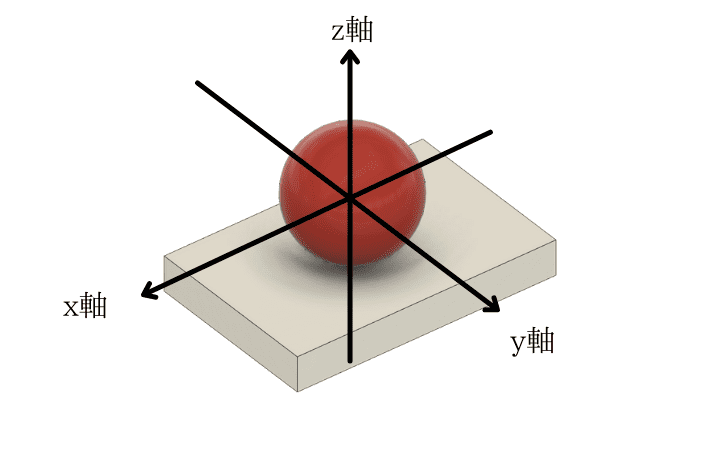
球が平板に接している状態を考えます
上の図だと、z軸方向には移動することができません(球同士が離れてしまうため)
他の方向の移動や回転はできるため、点対偶の自由度は\(6-1 = 5\)となります
「自由度5」のように呼びます
線対偶
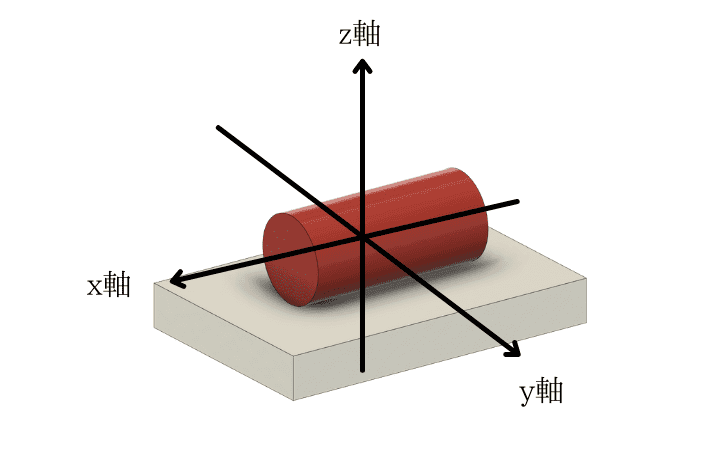
円柱が平板に接している状態を考えます
上の図だと、z軸方向の移動とx軸周りの回転ができません
よって、線対偶の自由度は\(6-2 = 4\)となります
面対偶

平板同士が接している状態を考えます
上の図だと、z方向の移動、x,y軸周りの回転運動ができません
よって、面対偶の自由度は\(6-3 = 3\)となります
滑り対偶
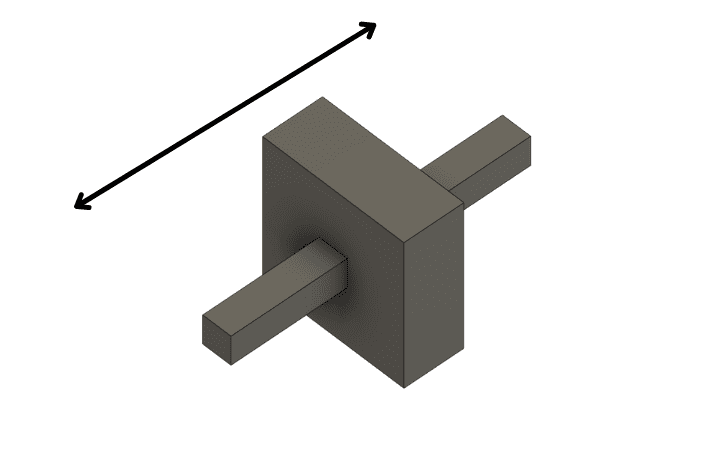
滑り対偶は一方向の移動しかできないので、自由度1になります
回り対偶
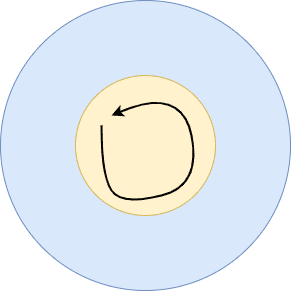
回り対偶は一方向の回転しかできないので、自由度1になります
ねじ対偶
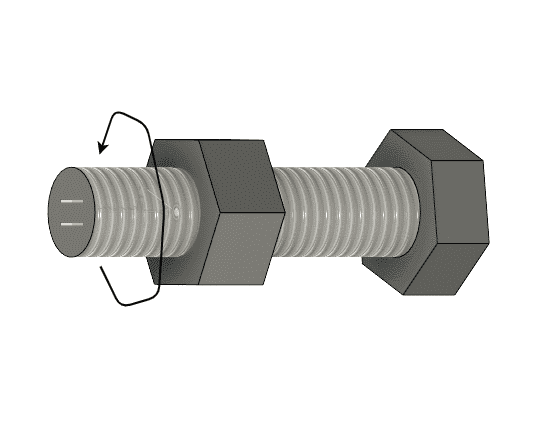
ねじ対偶は一方向の回転しかできないため、自由度1になります
球面対偶

図のような球面対偶は全ての軸周りの回転運動が可能であり、全ての軸方向への移動はできないため、自由度は3になります
ものによってはジョイント部でねじり回転ができないため、自由度は2になります
【参考】
https://monoist.atmarkit.co.jp/mn/articles/1104/15/news003_3.html
https://www.keyence.co.jp/ss/products/measure-sys/machine-elements/link/type.jsp
https://ja.wikipedia.org/wiki/%E5%AF%BE%E5%81%B6_(%E6%A9%9F%E6%A2%B0%E5%B7%A5%E5%AD%A6)
https://www.ikont.co.jp/product/needle/ndl09.html