以下の図のような球のz軸まわりの慣性モーメントを求める
密度はρ、質量はm、半径はRとする
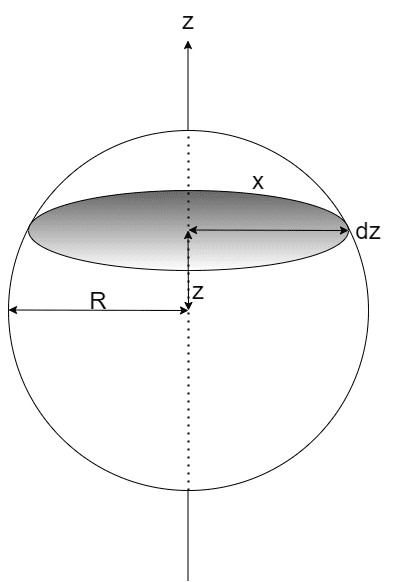
球をz軸に垂直な平面でスライスして、円板にする
その円板の慣性モーメントを求め、積分していくというやり方で解いていく
スライスした円板の半径xは
$$x^2 = R^2 - z^2$$
スライスした薄い円板の質量は
$$dm = \rho \pi (R^2 - z^2)dz$$
円板のz軸まわりの慣性モーメントはこちらの記事より
$$\frac{1}{2}mR^2$$
であるから、スライスした部分の慣性モーメントは
$$dI_{z} = \frac{1}{2}\rho \pi (R^2 - z^2)(\sqrt{R^2 - z^2})^2 dz = \frac{1}{2}\rho \pi (R^2 - z^2)^2 dz$$
dzを-R～Rまで積分すれば球の慣性モーメントが求められるので
$$\begin{align*}
I
&= \frac{1}{2}\rho \pi \int_{-R}^{R} (R^2 - z^2)^2 dz\\
&= \frac{1}{2}\rho \pi \int_{-R}^{R} (R^4 - 2R^2 z^2 + z^4) dz\\
&= \frac{1}{2}\rho \pi \left[ R^4 z -\frac{2}{3}R^2 z^3 + \frac{z^5}{5} \right]_{-R}^{R}\\
&= \rho \pi (R^5 - \frac{2}{3}R^5 + \frac{R^5}{5})\\
&= \frac{8}{15}\rho \pi R^5
\end{align*}
$$
ここで$$\rho = \frac{3m}{4\pi R^3}$$より
$$I = \frac{2}{5}mR^2$$
回転半径は$$k = \sqrt{\frac{I}{m}} = \sqrt{\frac{2}{5}}R$$