この記事では、対数グラフについて簡単に説明します
対数グラフと対数目盛
対数グラフとは、対数目盛を使ったグラフのことです
一般的なグラフでは、目盛は「0,1,2,3…」や「0,10,20,30…」のように一定距離ごとに一定数増えていきますが、対数目盛は「0,10,100」などのように、一定距離ごとに\(n\)倍ずつ増えていきます
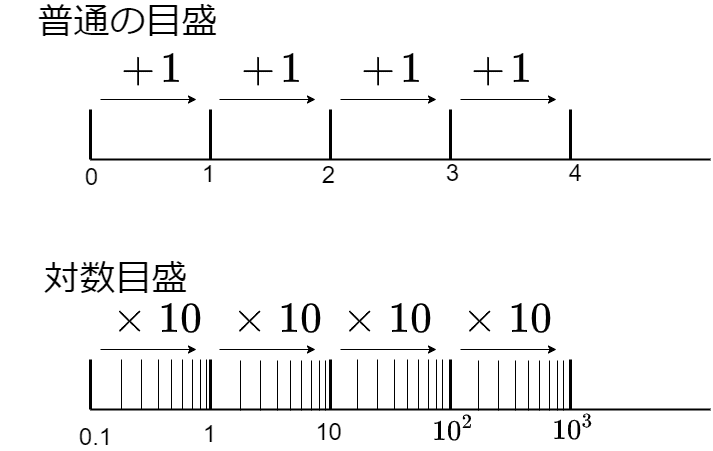
対数目盛の偏りについては後で説明します
そして、この対数目盛がx,y軸のどちらかのみに付いているものを片対数グラフ、両方に付いているものを両対数グラフと呼びます

この図では、片対数グラフは縦軸が普通の目盛、横軸が対数目盛となっています
対数グラフを使うメリット
対数グラフは、様々な桁数のデータを確認するときに便利です
例えば指数関数的に値が増えていくとき、普通の目盛を使うと、最初の方のプロットがとても小さく表示されてしまい、詳細が分かりません
そのようなときに対数目盛を使うと、様々な桁数の数値が一目で確認できるようになります
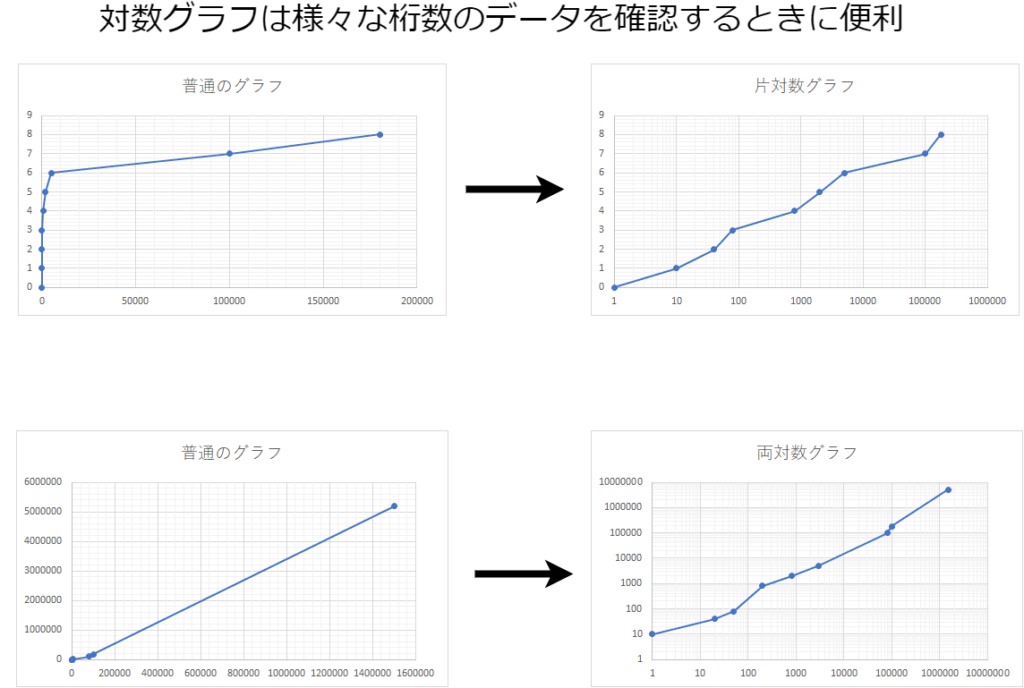
目盛の読み方
対数グラフの偏った目盛の読み方について説明します

上図ですと、対数目盛は10倍されるまでに徐々に目盛が短くなっていき、10倍される度にそれを繰り返していますね
対数目盛は「0,10,100」などのように、一定距離ごとに\(n\)倍ずつ増えていくため、このような目盛間隔になっています
例えば、2倍される距離を見てみると

このように、どこを取っても同じ距離であることが分かります
これは、2倍だけでなく、3倍でも10倍のような他の倍率でも当てはまります
まとめ
対数目盛は、一定距離ごとに\(n\)倍ずつ増えていく
この対数目盛がx,y軸のどちらかのみに付いているものが片対数グラフ、両方に付いているものが両対数グラフ
対数グラフは、様々な桁数のデータを確認するときに便利