制御工学では、伝達関数を使って、入力信号から出力信号を求めることをします
これまでは、インパルス入力、単位ステップ入力、ランプ入力などの入力信号について説明しました
他にもよく使われるものとして、正弦波(sin波)があります
この記事では、正弦波の入力に対しての応答(周波数応答)、正弦波を入力したときの伝達関数(周波数伝達関数)と周波数特性について説明します
周波数伝達関数
要素の伝達関数\(G(s)\)の\(s\)を\(j\omega\)に置き換えた\(G(j\omega )\)を周波数伝達関数と呼びます
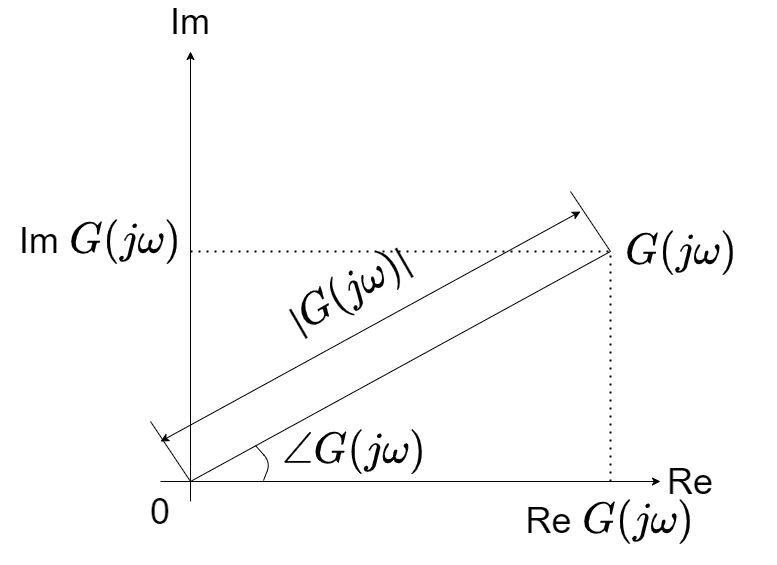
周波数伝達関数を複素平面上に表すと、以下のようになります
一次遅れ系の周波数伝達関数
一次遅れ系の周波数伝達関数は、一次遅れ系の伝達関数\(G(s)\)の\(s\)を\(j\omega\)に置き換えれば求められます
一次遅れ系の伝達関数は
$$G(s) = \frac{K}{1+Ts}$$
であるから、一次遅れ系の周波数伝達関数は
$$G(j\omega ) = \frac{K}{1+j\omega T}$$
となります
分母を有利化すると
$$\begin{align*}
G(j\omega )
&=\frac{K}{1+j\omega T}\\
&= \frac{K(1-j\omega T)}{(1+j\omega T)(1-j\omega T)}\\
&= \frac{K-Kj\omega T}{1+(\omega T)^2}\\
&= \frac{K}{1+(\omega T)^2} - j\frac{K\omega T}{1+(\omega T)^2}
\end{align*}$$
のようになります
二次遅れ系の周波数伝達関数
二次遅れ系の周波数伝達関数は、二次遅れ系の伝達関数\(G(s)\)の\(s\)を\(j\omega\)に置き換えれば求められます
二次遅れ系の伝達関数は
$$G(s) = \frac{K\omega _{n}^2}{s^2 + 2\zeta \omega _{n}s + \omega _{n}^2}$$
であるから、二次遅れ系の周波数伝達関数は
$$\begin{align*}
G(j\omega )
&= \frac{K\omega _{n}^2}{s^2 + 2\zeta \omega _{n}s + \omega _{n}^2}\\
&=\frac{K\omega _{n}^2}{(j\omega )^2 + 2\zeta \omega _{n}j\omega + \omega _{n}^2}\\
&=\frac{K\omega _{n}^2}{-\omega ^2 + \omega _{n}^2 + j2\zeta \omega _{n}\omega}
\end{align*}$$
となります
周波数応答
正弦波の入力に対しての応答を周波数応答と呼びます
例えば、あるシステムに正弦波\(u(t) = A\sin{\omega t}\)を入力したとすると、以下のように周波数伝達関数により\(B\sin{(\omega t - \phi)}\)信号が出力されます

要素が線形であれば、出力は入力と同じ周波数の正弦波になりますが、振幅と位相は周波数によって異なります
周波数応答\(y(t)\)は\(G(j\omega )\)を使って、以下のような式で表されます
$$y(t) = |G( j\omega )|A\sin{(\omega t + \angle G(j\omega ))}\cdots ①$$
\(|G( j\omega )|\)は、\(G(j\omega )\)の大きさ、\(\angle G(j\omega )\)は、\(G(j\omega )\)の偏角(位相)と呼び、以下の式で表されます
$$|G(j\omega )| = \sqrt{|Re~G(j\omega )|^2 + |Im~G(j\omega )|^2}$$
$$\angle G( j\omega ) = \tan ^{-1}\frac{Im~G(j\omega )}{Re~G(j\omega )}$$
一次遅れ系の周波数応答
上述したように、一次遅れ系の周波数伝達関数は
$$G(j\omega ) = \frac{K}{1+(\omega T)^2} - j\frac{K\omega T}{1+(\omega T)^2}$$
であるから、大きさと偏角はそれぞれ
$$\begin{align*}
|G(j\omega )| &= K\sqrt{(\frac{1}{1+(\omega T)^2})^2 + (- \frac{\omega T}{1+(\omega T)^2})^2}\\
&= \frac{K}{\sqrt{1+(\omega T)^2}}
\end{align*}$$
$$\begin{align*}
\angle G( j\omega )
&= \tan ^{-1}\frac{Im~G(j\omega )}{Re~G(j\omega )}\\
&= \tan ^{-1}\frac{-\frac{K\omega T}{1+(\omega T)^2}}{\frac{K}{1+(\omega T)^2}}\\
&= -\tan ^{-1} \omega T
\end{align*}$$
となります
これらを①に代入すれば、周波数応答\(y(t)\)を求めることができます
$$\begin{align*}
y(t)
&= |G( j\omega )|A\sin{(\omega t + \angle G(j\omega ))}\\
&=\frac{K}{\sqrt{1+(\omega T)^2}}A\sin{(\omega t -\tan ^{-1} \omega T)}
\end{align*}$$
もう少し簡単な方法
上記の方法でも、大きさや偏角は求められますが、もう少し計算を簡単にする方法があります
1.分母と分子、それぞれの大きさと偏角を求める
2.\(|G(j\omega)| = \frac{分子の大きさ}{分母の大きさ}\)で大きさが求められる
3.\(\angle G(j\omega) = 分子の偏角 - 分母の偏角\)で偏角が求められる
一次遅れ系の伝達関数の大きさと偏角を求めてみます
1.分子の大きさは\(K\)、分母の大きさは\(\sqrt{1+(T\omega)^2}\)となり、分子の偏角は\(0\)、分母の偏角は\(\tan ^{-1}(\frac{T\omega}{1})\)となります
2.$$\begin{align*}
|G(j\omega)|
&= \frac{分子の大きさ}{分母の大きさ}\\
&= \frac{K}{\sqrt{1+(\omega T)^2}}
\end{align*}$$
3.$$\begin{align*}
\angle G( j\omega )
&= 分子の偏角 - 分母の偏角\\
&= -\tan ^{-1} \omega T
\end{align*}$$
この方法であれば、周波数伝達関数の分母を実数化する必要がなくなります
二次遅れ系の周波数応答
簡単な方法で、大きさと偏角を求めてみます
分子の大きさは\(K\omega ^2\)
分母の大きさは
$$\sqrt{(\omega _{n}^2 - \omega ^2)^2 + (2\zeta \omega _{n}\omega)^2}$$
分子の偏角は\(0\)
分母の偏角は
$$-\tan ^{-1}(\frac{2\zeta \omega _{n}\omega}{\omega _{n}^2 - \omega ^2})$$
よって
$$|G(j\omega)| = \frac{K\omega _{n}^2}{\sqrt{(\omega _{n}^2 - \omega ^2)^2 + (2\zeta \omega _{n}\omega)^2}}$$
$$\angle G( j\omega ) = -\tan ^{-1}(\frac{2\zeta \omega _{n}\omega}{\omega _{n}^2 - \omega ^2})$$
のようになります
周波数特性
あるシステムに正弦波\(u(t) = A\sin{\omega t}\)を入力したならば、出力信号が\(B\sin{(\omega t - \phi)}\)になるように、周波数は同じでも、振幅と位相が異なった値として出力されます
このような振幅の変化や位相の変化の特性のことを周波数特性と呼びます
指標の一つとしてゲインというものがあり、ゲイン\(g\)は以下の式で表されます
$$g = 20\log _{10}\frac{B}{A} = 20\log _{10}|G(j\omega)|$$
ゲインは、入力と出力の振幅比の常用対数を20倍したものです
ゲインの単位はデシベル[dB]です
工事の音などの騒音問題などで聞くものと同じですが、デシベルは音の分野だけではなく制御や計測の分野でも使用されています
まとめ
要素の伝達関数\(G(s)\)の\(s\)を\(j\omega\)に置き換えた\(G(j\omega )\)を周波数伝達関数と呼ぶ
正弦波の入力に対しての応答が周波数応答\(y(t)\)である
$$y(t) = |G( j\omega )|A\sin{(\omega t + \angle G(j\omega ))}$$
求め方は
1.分母と分子、それぞれの大きさと偏角を求める
2.\(|G(j\omega)| = \frac{分子の大きさ}{分母の大きさ}\)で大きさが求められる
3.\(\angle G(j\omega) = 分子の偏角 - 分母の偏角\)で偏角が求められる
振幅の変化や位相の変化の特性のことを周波数特性と呼ぶ
ゲイン\(g\)は以下の式で表される
$$g = 20\log _{10}\frac{B}{A}= 20\log _{10}|G(j\omega)|$$