ヘロンの公式は、三角形の3辺の長さから面積を求める公式です
以下の三角形ABCの面積Sは
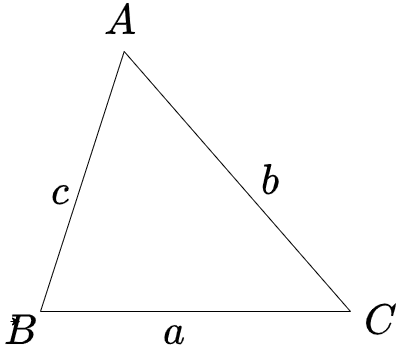
今回は、この公式の「三角関数を使って証明する方法」と「中学数学だけで証明する方法」の2種類の証明方法を紹介していきます
三角関数を使って証明する方法
前回の記事より、三角形の面積はsinを使って
$$S = \frac{1}{2}ab\sin{C}$$
と表せます
これと、余弦定理$$c^2 = a^2 + b^2 -2ab\cos{C}$$を使います
三角形の面積Sは
$$\begin{align*}
S
&= \frac{1}{2}ab\sin{C}\\
&= \frac{1}{2}ab\sqrt{1-\cos ^2 C}\\
&= \frac{1}{2}ab\sqrt{1 - (\frac{a^2 + b^2 -c^2}{2ab})^2}\\
&= \frac{1}{2}ab\cdot\frac{1}{2ab}\sqrt{(2ab)^2 - (a^2 + b^2 - c^2)^2}\\
&= \frac{1}{4}\sqrt{(2ab + a^2 + b^2 -c^2)(2ab - a^2 - b^2 + c^2)}\\
&= \frac{1}{4}\sqrt{\{(a+b)^2 - c^2\}\{(c^2 - (a - b)^2)\}}\\
&= \frac{1}{4}\sqrt{(a+b+c)(a+b-c)(a-b+c)(-a+b+c)}\\
&= \sqrt{\frac{a+b+c}{2} \cdot \frac{-a+b+c}{2} \cdot \frac{a-b+c}{2} \cdot \frac{a+b-c}{2}}\\
ここで、s = \frac{a+b+c}{2}とすると\\
&= \sqrt{s(s-a)(s-b)(s-c)}
\end{align*}$$
と、証明できました
中学数学の知識で証明する
中学数学では、三角関数や余弦定理について学ばないので、これらを使わずに証明していきます
三角形ABCの頂点Aから線分BCに垂線を下ろし、交点をHとします
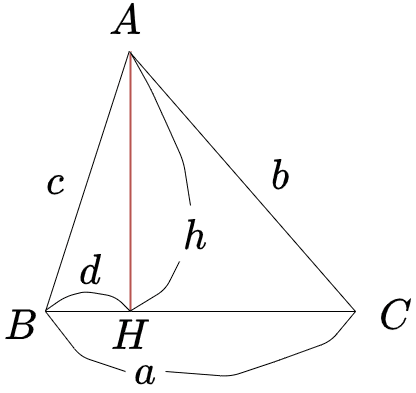
AH = h , BH = dとおきます
\(\triangle ABHと \triangle AHC\)において、三平方の定理より
$$\begin{align*}
&c^2 = h^2 + d^2\cdots ①\\
&b^2 = h^2 + (a-d)^2\cdots ②
\end{align*}$$
②を変形して
$$\begin{align*}
&b^2 = h^2 + a^2 - 2ad + d^2\\
&h^2 = b^2 - a^2 + 2ad - d^2\cdots ③
\end{align*}$$
③を①に代入して
$$\begin{align*}
&c^2 = b^2 - a^2 + 2ad\\
&d = \frac{a^2 - b^2 + c^2}{2a}\cdots ④
\end{align*}$$
④を①に代入すると
$$c^2 = h^2 + \frac{(a^2 - b^2 + c^2)^2}{4a^2}$$
$$\begin{align*}
h^2
&= c^2 - \frac{(a^2 - b^2 + c^2)^2}{4a^2}\\
&= \frac{4a^2 c^2 - (a^2 - b^2 + c^2)^2}{4a^2}\\
&= \frac{(2ac)^2 - (a^2 - b^2 + c^2)^2}{4a^2}\\
&= \frac{\{2ac + (a^2 - b^2 + c^2)\}\{2ac - (a^2 - b^2 + c^2)\}}{4a^2}\\
&= \frac{(a^2 + 2ac + c^2 - b^2)(b^2 -a^2 + 2ac - c^2)}{4a^2}\\
&= \frac{\{(a+c)^2 - b^2\}\{b^2 - (a- c)^2\}}{4a^2}\\
&= \frac{(a+c+b)(a+c-b)\{b-(a-c)\}\{b+(a-c)\}}{4a^2}\\
&= \frac{(a+c+b)(a+c-b)(-a+b+c)(a+b-c)}{4a^2}\\
&= \frac{(a+b+c)(-a+b+c)(a-b+c)(a+b-c)}{4a^2}
\end{align*}$$
さらに、\(s = \frac{a+b+c}{2}\)とすると
$$\begin{align*}
h^2
&= \frac{2s(2s-2a)(2s-2b)(2s-2c)}{4a^2}\\
&= \frac{4}{a^2}s(s-a)(s-b)(s-c)
\end{align*}$$
h > 0であるから
$$\begin{align*}
h
&= \sqrt{\frac{4}{a^2}s(s-a)(s-b)(s-c)}\\
&= \frac{2}{a}\sqrt{s(s-a)(s-b)(s-c)}
\end{align*}$$
これで、三角形の高さhが求められました
よって、三角形の面積Sは
$$\begin{align*}
s
&= \frac{a\cdot h}{2}\\
&= \frac{1}{2}\cdot a \cdot \frac{2}{a}\sqrt{s(s-a)(s-b)(s-c)}\\
&= \sqrt{s(s-a)(s-b)(s-c)}
\end{align*}$$
となり、ヘロンの公式が導出できました
まとめ
ヘロンの公式の2種類の導出方法について説明しました
三角関数を使わない方法でも導出できるので、まだ高校数学を学んでいない方も参考にしてみてください

