この記事では、制御工学を勉強する前に知っておきたい複素数について簡単に説明します
高校数学の復習用としてお使いください
複素数
2乗すると正になる数を実数、2乗すると負になる数を虚数、実数と虚数の和を複素数と呼び、\(z = a + bi\)のような形で表されます
iは虚数単位で、\(i^2 = -1\)の性質を持っています (iはjと記述されることもあります)
\(a,b,c,d\)を実数としたとき、以下のような性質があります
$$\begin{align*}
a+bi = 0 &\rightarrow a = 0~,~b=0\\
a+bi = c+di &\rightarrow a=c~,~b=d
\end{align*}$$
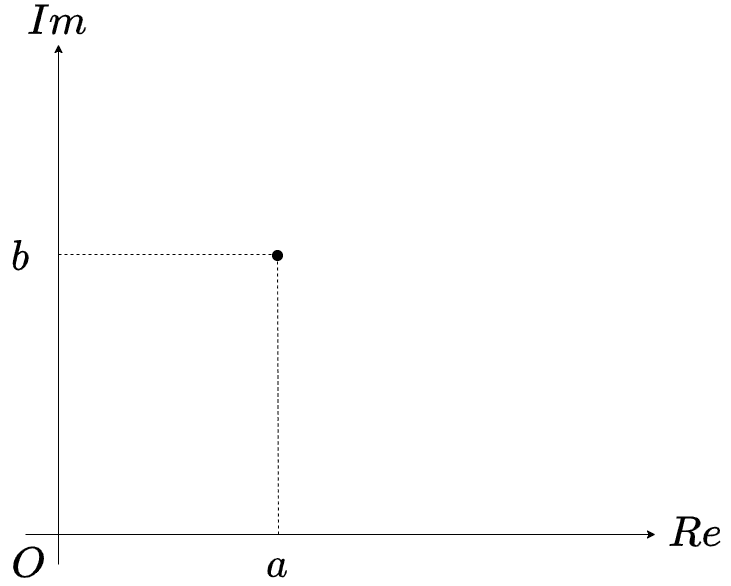
横軸を実軸、縦軸を虚軸とした複素平面では、複素数は点またはベクトルで記述されます(Imは虚数の英語 Imaginary number、Reは実数の英語Real numberに由来しています)
極座標
複素平面上にある複素数\(z = a + bi\)が、x軸の正の部分を\(\theta\)だけ反時計回りに回転させた線と半径rの円の交点にあるとします

このとき、\(a=r\cos{\theta}~,~b=r\sin{\theta}\)であるため
オイラーの公式\(e^{i\theta} = \cos{\theta} + i\sin{\theta}\)を使うと複素数は
$$\begin{align*}
z
&= a+bi = r\cos{\theta} + r\sin{\theta}\\
&= r(\cos{\theta} + \sin{\theta}) = re^{i\theta}
\end{align*}$$
のように表されます、このような表現を極形式と言います
\(r\)を\(z\)の絶対値、\(\theta\)を\(z\)の偏角と言います
$$r=|z| = \sqrt{a^2 + b^2}~,~\theta = \angle{z} = \tan ^{-1}\frac{b}{a}$$
練習問題
簡単な練習問題をやってみましょう
次の(1)~(3)の計算をして\(a+bi\)の形で表せ、また(4)を極形式で表せ
(1)$$(2-i)+(4+2i)$$
(2)$$(5+3i)(2-i)$$
(3)$$\frac{2+i}{1-i}$$
(4)$$\sqrt{3}+i$$
【解答】
(1)
$$(2-i)+(4+2i) = 6+i$$
(2)
$$\begin{align*}
(5+3i)(2-i)
&= 10 - 5i + 6i +3\\
&= 13 + i
\end{align*}$$
(3)
$$\begin{align*}
\frac{2+i}{1-i}
&= \frac{(2+i)(1+i)}{(1-i)(1+i)}\\
&= \frac{2+3i-1}{2}\\
&= \frac{1}{2} + \frac{3}{2}i
\end{align*}$$
(4)
$$r = \sqrt{\sqrt{3}^2+1^2} = 2$$
$$\theta = \tan ^{-1}\frac{1}{\sqrt{3}} = \frac{\pi}{6}$$
よって
$$\sqrt{3}+i = 2e^{i\frac{\pi}{6}}$$