はりの曲げの問題は、たわみとたわみ角を求める問題が多く、基本的に
1. せん断力と曲げモーメントを求める
2. たわみの微分方程式に代入
3. 境界条件
と進めていけば解けます
ですが、定期試験や大学院試験では、時間が不足することを防ぐため、検算をするために、公式を覚えていくことをおすすめします
先端荷重、等分布荷重、先端曲げモーメントのたわみ、たわみ角で計6つなので、そこまで大変ではないと思います
符号については、右側断面で下方向に働くせん断力を正、梁が下向きに凸となる曲げモーメントを正としています
公式
| はり | せん断力F , 曲げモーメントM | たわみy , たわみ角θ |
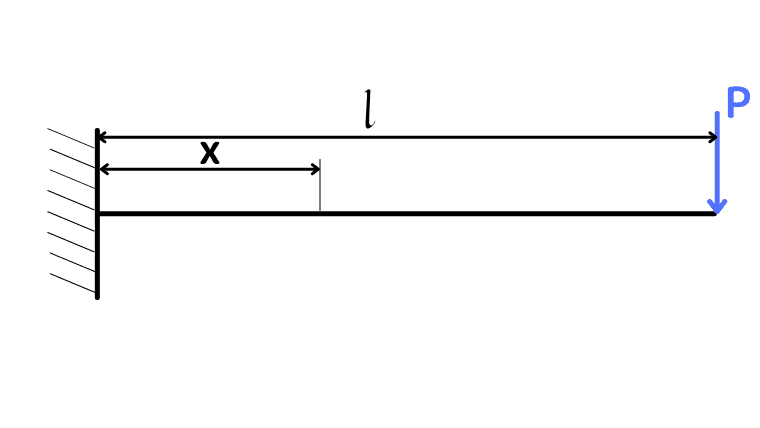
| 先端荷重
| $$F = P$$ $$M = - P(l-x)$$ | $$y = \frac{Pl^3}{6EI}(3 - \frac{x}{l})\frac{x^2}{l^2} \\ y_{max} = y_{x = l} = \frac{Pl^3}{3EI}$$ $$\theta = \frac{Pl^3}{2EI}(2 - \frac{x}{l})\frac{x}{l} \\ \theta _{max} = \theta _{x = l} = \frac{Pl^2}{2EI}$$ |
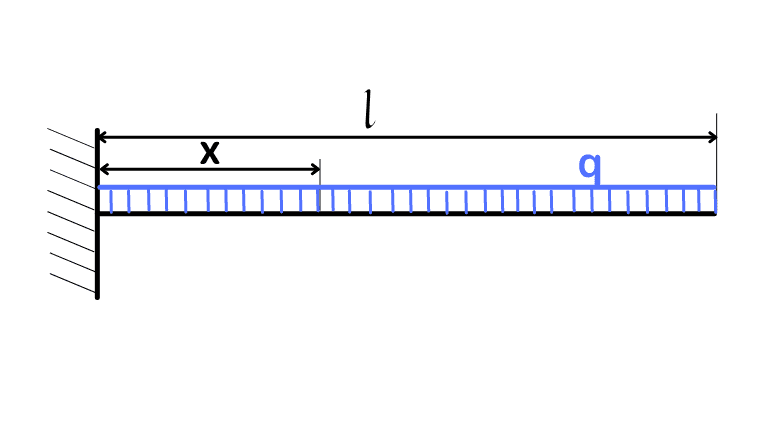
| 分布荷重
| $$F = q(l - x)$$ $$M = -\frac{q}{2}(l -x)^2$$ | $$y = \frac{ql^2}{24EI}x^{2}(6-4\frac{x}{l}+\frac{x^2}{l^2}) \\ y_{max} = y_{x=l} = \frac{ql^4}{8EI}$$ $$\theta = \frac{ql^2}{6EI}x(3-3\frac{x}{l}+\frac{x^2}{l^2}) \\ \theta _{max} = \theta _{x=l} = \frac{ql^3}{6EI}$$ |
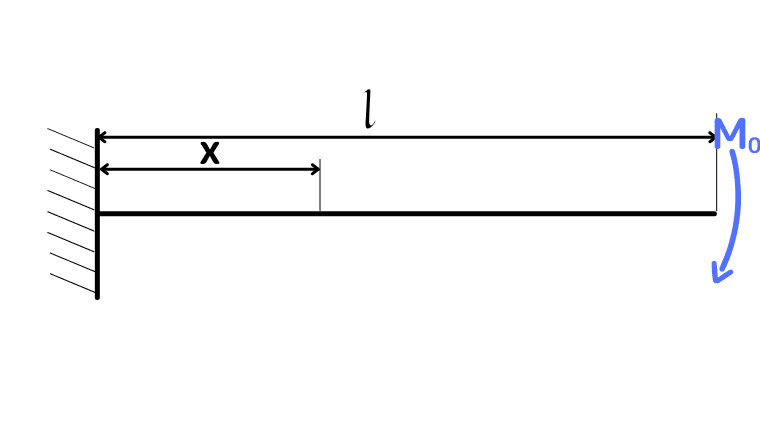
| 先端曲げモーメント
| $$F = 0$$ $$M = -M_0$$ | $$y = \frac{M_{0}}{2EI}x^2 \\ y_{max} = y_{x=l} = \frac{M_{0}l^2}{2EI}$$ $$\theta = \frac{M_{0}}{EI}x \\ \theta _{max} = \theta _{x=l} = \frac{M_{0}l}{EI}$$ |
色々と書いてますが、覚えるところはそれぞれのy_max , θ_maxの部分です
すぐに覚えられると思うので、ぜひ覚えてみると良いと思います
定期試験や大学院入試では先端のたわみやたわみ角を求める問題が多いので、きっと役に立つはずです