円柱、円板のそれぞれの軸まわりの慣性モーメントを求めます
円柱や円板の法線軸方向以外の慣性モーメントの求め方は、導出方法が載っているページがあまりなかったので、私が導出方法を解説していきます
円板の慣性モーメント
以下のような円板の慣性モーメントを求めます
質量はm、密度はρとし、tは非常に小さいものとします
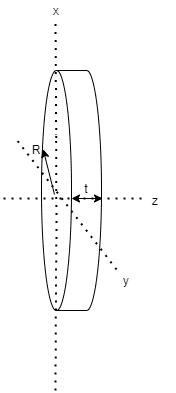
まずは円板に垂直な軸まわりの慣性モーメントから求めます、円板に垂直な方向から見た図を考えて
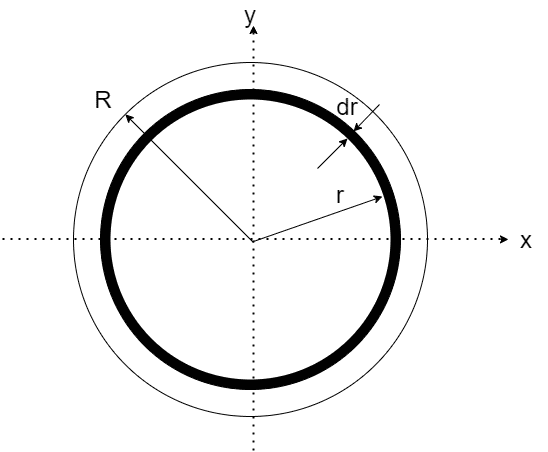
上図の微少な幅drの質量dmは
積分範囲は0~Rである
よって慣性モーメントは
$$\begin{align*}
I_{z}
&= \int_0^R r^2 \cdot \frac{2mr}{R^2} dr\\
&= \int_0^R \frac{2mr^3}{R^2} dr\\
&= \frac{2m}{R^2} \int_0^R r^3 dr\\
&= \frac{2m}{R^2}\left[ \frac{r^4}{4}\right]_0^R\\
&= \frac{mR^2}{2}
\end{align*}$$
直交軸の定理と対称性から$$I_{z} = I_{x} + I_{y}~~~I_{x} = I_{y}$$
よって$$I_{x} = I_{y} = \frac{1}{2}I_{z} = \frac{1}{4}mR^2\cdots ①$$
円柱の慣性モーメント
以下のような円柱のそれぞれの軸の慣性モーメントを求めます
質量はm、密度はρとして考えます

c軸まわりの慣性モーメントは円板と同じように求められます
$$I_{c} = \frac{mR^2}{2}$$
以下の図のように厚みdcのスライスした円板の質量dmは
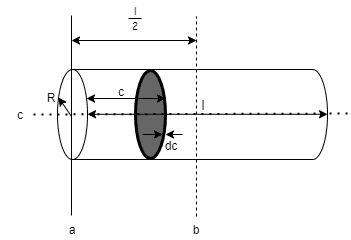
①より$$dI = \frac{R^2}{4}\frac{m}{l}dc = \frac{mR^2}{4l}dc$$
平行軸の定理より、a軸まわりの慣性モーメントは
$$dI_{a} = (\frac{mR^2}{4l} + \frac{m}{l}y^2)dc$$
$$\begin{align*}
I_{a}
&= \int_0^l (\frac{mR^2}{4l} + \frac{m}{l}c^2)dc\\
&= \frac{mR^2}{4} + \frac{ml^2}{3}
\end{align*}$$
b軸まわりの慣性モーメントは、平行軸の定理より
$$I_{b} = I_{a} - (\frac{l}{2})^2 m = \frac{mR^2}{4} + \frac{ml^2}{12}$$
まとめ
回転半径を$$k = \sqrt{\frac{I}{m}}$$から求めると
| 物体 | 慣性モーメント | 回転半径 |
| 円板
| $$I_{x} = \frac{1}{4}mR^2$$ | $$k_{x} = \frac{R}{2}$$ |
| $$I_{y} = \frac{1}{4}mR^2$$ | $$k_{y} = \frac{R}{2}$$ | |
| $$I_{z} = \frac{1}{2}mR^2$$ | $$k_{z} = \frac{R}{\sqrt{2}}$$ | |
| 円柱
| $$I_{a} = \frac{mR^2}{4} + \frac{ml^2}{3}$$ | $$k_{a} = \sqrt{\frac{R^2}{4} + \frac{l^2}{3}}$$ |
| $$I_{b} = \frac{mR^2}{4} + \frac{ml^2}{12}$$ | $$k_{b} = \sqrt{\frac{R^2}{4} + \frac{l^2}{12}}$$ | |
| $$I_{c} = \frac{mR^2}{2}$$ | $$k_{c} = \frac{R}{\sqrt{2}}$$ |
注意
円板の厚さtを無視するかどうかは、問題文の条件によって異なります
厚さを微少として無視しない場合は、円柱と同じ方法で慣性モーメントを求められます