代表的な物体の慣性モーメントと回転半径をまとめました
| 形状 | 慣性モーメント | 回転半径 |
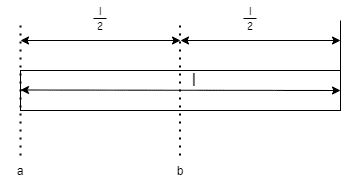
細棒
| $$I_{a} = \frac{m}{3}l^2$$ $$I_{b} = \frac{m}{12}l^2$$ | $$k_{a} = \frac{l}{\sqrt{3}}$$ $$k_{b} = \frac{l}{2\sqrt{3}}$$ |
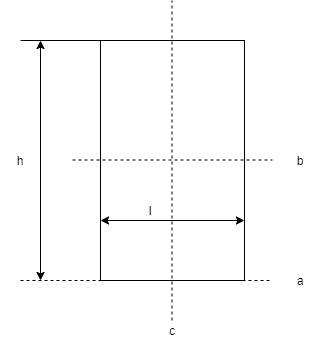
| 長方形
| $$I_{a} = \frac{mh^2}{3}$$ $$I_{b} = \frac{mh^2}{12}$$ $$I_{c} = \frac{ml^2}{12}$$ | $$k_{a} = \frac{h}{\sqrt{3}}$$ $$k_{b} = \frac{h}{2\sqrt{3}}$$ $$k_{c} = \frac{l}{2\sqrt{3}}$$ |
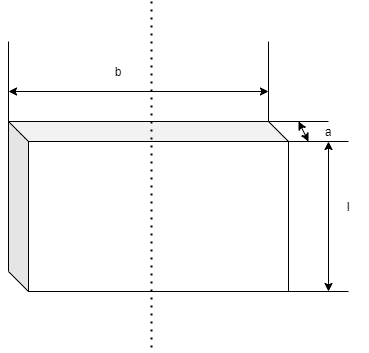
直方体
| $$I = \frac{1}{12}m(a^2 + b^2)$$ | $$k = \sqrt{\frac{a^2 + b^2}{12}}$$ |
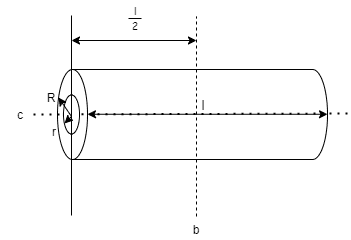
円柱
| $$I_{a} = m(\frac{l^2}{3}+\frac{R^2}{4})$$ $$I_{b} = m(\frac{l^2}{12}+\frac{R^2}{4})$$ $$I_{c} = \frac{1}{2}mR^2$$ | $$k_{a} = \sqrt{\frac{l^2}{3} + \frac{R^2}{4}}$$ $$k_{b} = \sqrt{\frac{l^2}{12}+\frac{R^2}{4}}$$ $$k_{c} = \frac{R}{\sqrt{2}}$$ |
中空円柱
| $$I_{b} = m(\frac{l^2}{12}+\frac{R^2 + r^2}{4})$$ $$I_{c} = \frac{1}{2}m(R^2 + r^2)$$ | $$\sqrt{\frac{l^2}{12}+\frac{R^2 + r^2}{4}}$$ $$\sqrt{\frac{R^2 + r^2}{2}}$$ |
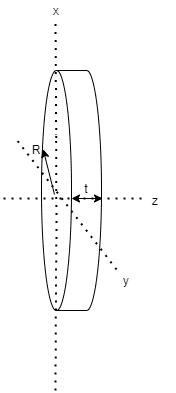
薄い円板
| $$I_{x} = \frac{1}{4}mR^2$$ $$I_{y} = \frac{1}{4}mR^2$$ $$I_{z} = \frac{1}{2}mR^2$$ | $$k_{x} = \frac{R}{2}$$ $$k_{y} = \frac{R}{2}$$ $$k_{z} = \frac{R}{\sqrt{2}}$$ |
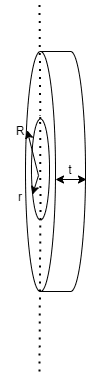
薄い中空円柱
| $$I = \frac{1}{4}m(R^2 + r^2)$$ | $$k = \frac{\sqrt{R^2 + r^2}}{2}$$ |
球
| $$I = \frac{2}{5}mR^2$$ | $$k = \sqrt{\frac{2}{5}}R$$ |
三角形板
| $$I_{a} = \frac{1}{6}mh^2$$ $$I_{b} = \frac{1}{18}mh^2$$ $$I_{c} = \frac{1}{18}m(l^2 - nl + n^2)$$ $$I_{z} = \frac{m}{18}(l^2 - ln + n^2 + h^2)$$(z軸は紙面垂直方向) | $$k_{a} = \frac{h}{\sqrt{6}}$$ $$k_{b} = \frac{h}{3\sqrt{2}}$$ $$k_{c} = \frac{1}{3}\sqrt{\frac{l^2 - nl + n^2}{2}}$$ $$k_{z} = \frac{1}{3}\sqrt{\frac{l^2 - ln + n^2 + h^2}{2}}$$ |
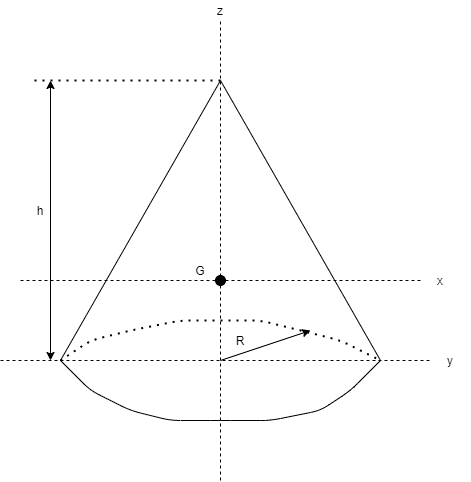
円錐
| $$I_{x} = \frac{3m}{80}(4R^2 + h^2)$$ $$I_{y}= \frac{3}{20}mR^2 + \frac{1}{10}mh^2$$ $$I_{z} = \frac{3}{10}mR^2$$ | $$k_{x} = \frac{1}{4}\sqrt{\frac{3(4R^2 + h^2)}{5}}$$ $$k_{y} = \frac{1}{2}\sqrt{\frac{3R^2 + 2h^2}{5}}$$ $$k_{z} = \sqrt{\frac{3}{10}}R$$ |
【導出方法】
それぞれの導出方法を解説しています
計算ミス等ありましたらお知らせください