入力信号を加えてから,出力信号が生じるまでの時間をむだ時間と呼びます
むだ時間を\(\tau\)とすると、むだ時間要素の伝達関数は
$$G(s) = e^{-\tau s}$$
となります
指数関数は線形ではないため、これをScilabで記述してボード線図を描こうとすると、エラーが発生します
Scilabでむだ時間要素のボード線図を描くためには、線形近似をする必要があります
この記事では、線形近似のパデ近似というものについて解説し、パデ近似を使ってむだ時間要素のボード線図を描いていきます
パデ近似
パデ近似の考え方は、むだ時間要素の伝達関数\(e^{-\tau s}\)を有理伝達関数\(G_{l}(s)\)に近似しようとするものです
$$G_{l}(s) = \frac{b_{m}s^{m}+b_{m-1}s^{m-1}+\cdots +b_{1}s^{1}+b_{0}}{a_{n}s^{n}+a_{n-1}s^{n-1}+\cdots +a_{1}s^{1}+a_{0}}\cdots ①$$
\(G_{l}(s) \approx e^{-\tau s}\)のような近似を目指します
\(e^{-s}\)をマクローリン展開すると
$$e^{-s} = 1 - s + \frac{s^2}{2!} - \frac{s^3}{3!} + \frac{s^4}{4!}\cdots②$$
となります
②でも近似はできていますが、①のような有利関数で表現したいので、sの係数ごとに\(n+m\)本の連立方程式を立式して、係数を求めることで\([n,m]\)次の近似を行います
例えば、[1,1]の近似であれば、まずは①をマクローリン展開して
$$\begin{align*}
G_{l}(s) &= \frac{b_{1}s+b_{0}}{a_{1}s+a_{0}}\\
&\approx \frac{b_{0}}{a_{0}} + \frac{a_{0}b_{1}-a_{1}b_{0}}{a_{0}^2}s + (\frac{a_{1}^{2}b_{0}}{a_{0}^3}+\frac{a_{1}b_{1}}{a_{0}^2})s^2 \cdots ③
\end{align*}$$
②,③の係数を比較すると
$$\begin{align*}
1 &= \frac{b_{0}}{a_{0}}\\
-1 &= \frac{a_{0}b_{1}-a_{1}b_{0}}{a_{0}^2}\\
\frac{1}{2} &= (\frac{a_{1}^{2}b_{0}}{a_{0}^3}+\frac{a_{1}b_{1}}{a_{0}^2})
\end{align*}$$
\(a_{0} = 1\)とすると係数は
$$a_{1} = \frac{1}{2}~,~b_{0} = 1~,~b_{1} = -\frac{1}{2}$$
のようになり、\(s \rightarrow \tau s\)とすると、以下のように[1,1]の近似ができました
$$e^{-\tau s} = \frac{1-\frac{\tau s}{2}}{1+\frac{\tau s}{2}}$$
[2,2]の近似も同様にして求められます
$$e^{-\tau s} = \frac{1-\frac{\tau s}{2}+\frac{(\tau s)^2}{12}}{1+\frac{\tau s}{2}+\frac{(\tau s)^2}{12}}$$
高次の近似を行えば精度は上がりますが、計算が面倒になるので次数の選び方には注意が必要です
むだ時間要素のボード線図の描き方
パデ近似した伝達関数を記述すれば、むだ時間要素のボード線図(もどき)を描くことができます
\(\tau = 0.01\)として、ボード線図(もどき)を描くと
1 2 3 4 | s = %s; Gs = (1-((0.01*s)/2)+((0.01*s)^2)/2)/(1+((0.01*s)/2)+((0.01*s)^2)/2); sys = syslin('c', Gs); bode(sys) |

ゲインはほぼ0[dB]であり、位相は周波数が大きくなるほど遅れが出ている、むだ時間要素のボード線図(もどき)を描くことができました
いい感じにズームを行えば
1 | zoom_rect([10^(-2), -180 , 10^(2), 180]) |
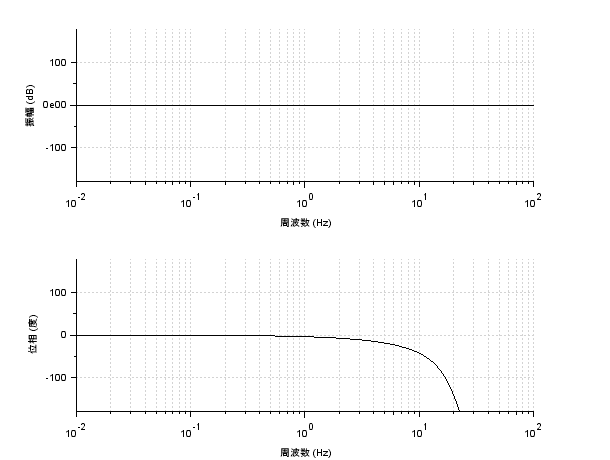
だいぶそれっぽくなっています
まとめ
この記事では、パデ近似を使ってむだ時間要素のボード線図を描いてみました
この記事で作成したボード線図は近似ですので、正確なボード線図ではありません
MATLABではパデ近似のための関数pade()が存在するため、MATLABを使う方が良いと思います
むだ時間要素のボード線図をScilabで描くのは、あまりおすすめできませんね