このページでは解答のみですので、問題は各々で手に入れてください
(過去問の入手方法等に関してはこちらの記事がおすすめです)
この解答が原因で発生した損失や損害について、こちらでは一切責任を負いかねます、参考資料の一つとしてお使いください
間違いのご指摘、質問等ありましたらお気軽にTwitter、この記事のコメント、メールどれかに連絡ください、書いた順で早く返事ができると思います
domeinshi(at)gmail.com
※(at)の部分は@にしてください
問題1
(1)$$\displaystyle \lim_{ n \to \infty } \frac{a^n}{b^n + 1} = \displaystyle \lim_{ n \to \infty } \frac{(\frac{a}{b})^n }{1 + \frac{1}{b^n}} = 0$$
(2)$$\begin{align*}
y'
&= (\frac{\sin{x}}{1+\cos{x}})' \\
&= \frac{\cos{x}(1+\cos{x}) + \sin{x}\sin{x}}{(1+\cos{x})^2}\\
&= \frac{1+\cos{x}}{(1+\cos{x})^2}\\
&= \frac{1}{1+\cos{x}}
\end{align*}$$
問題2
(1)
\int x^{2}e^{3x} dx
&= \int x^{2}(\frac{e^{3x}}{3})'dx\\
&= \frac{x^{2}e^{3x}}{3} - \frac{2}{9}\int x(e^{3x})' dx \\
&= \frac{x^{2}e^{3x}}{3} - \frac{2}{9}xe^{3x} + \frac{2}{9}\int e^{3x} dx\\
&= \frac{x^{2}e^{3x}}{3} - \frac{2}{9}xe^{3x} + \frac{2}{27}e^{3x}
\end{align*}$$
(2)
グラフにするとこのような感じになります
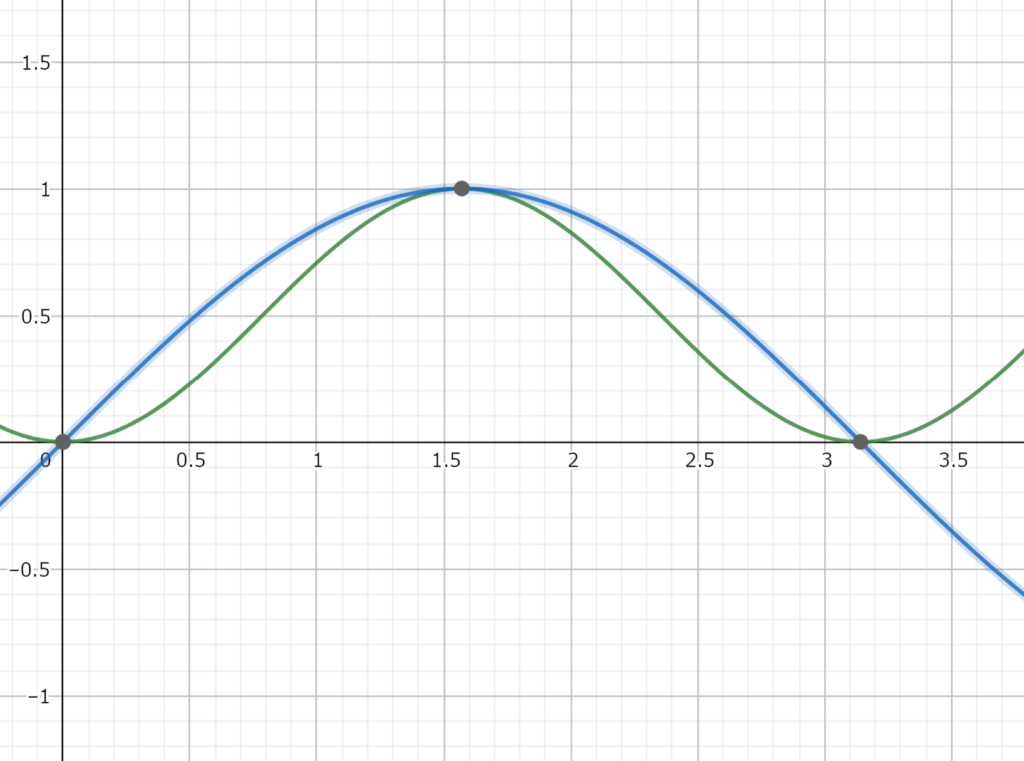 (引用:https://www.geogebra.org/graphing?lang=ja)
(引用:https://www.geogebra.org/graphing?lang=ja)
$$\sin{x} = \sin ^2{x}$$を整理すると$$\sin{x}(\sin{x} - 1) = 0$$$$x = 0 , \frac{\pi}{2}$$
求める面積は$$\begin{align*}
S
&= \int_0^{\frac{\pi}{2}} \sin{x}(1 - \sin{x})dx\\
&= \int_0^{\frac{\pi}{2}} -\frac{1+\cos{2x}}{2} + \sin{x}dx\\
&= \left[ \frac{x}{2} + \frac{\sin{2x}}{4} - \cos{x} \right]_0^\frac{\pi}{2}\\
&= -\frac{\pi}{4} + 1
\end{align*}
$$
問題3
(1)
(a)
より
$$|-A| = (-\lambda_1)(-\lambda_2)(-\lambda_3)(-\lambda_4)$$
また$$|-A| = (-1)^n|A|$$より$$|A| = \lambda_{1}\lambda_{2}\lambda_{3}\lambda_{4}$$
(b)
行列Aの変換方程式をPとすると
$$P^{-1}AP = \begin{bmatrix} \lambda_{1} &0&0&0\\0&\lambda_{2}&0&0\\0&0&\lambda{3}&0\\0&0&0&\lambda_{4} \end{bmatrix}$$
(2)
より行列Bは正則であり、掃き出し法により
[ B | E ]
&= \left[\begin{array}{rrr|rrr} 1 & 0 & 2 & 1 & 0 & 0 \\ 4 & 1 & -1 & 0 & 1 & 0 \\ -3 & 0 & 5 & 0 & 0 & 1 \end{array} \right]\\
&\rightarrow \left[\begin{array}{rrr|rrr} 1 & 0 & 2 & 1 & 0 & 0 \\ 0 & 1 & -9 & -4 & 1 & 0 \\ 0 & 0 & 1 & \frac{3}{11} & 0 & \frac{1}{11} \end{array} \right]\\
&\rightarrow \left[\begin{array}{rrr|rrr} 1 & 0 & 0 & \frac{5}{11} & 0 & -\frac{2}{11} \\ 0 & 1 & 0 & -\frac{17}{11} & 1 & \frac{9}{11} \\ 0 & 0 & 1 & \frac{3}{11} & 0 & \frac{1}{11} \end{array} \right]
\end{align*}$$
よって$$B^{-1} = \frac{1}{11}\begin{bmatrix} 5 & 0 & -2\\ -17 & 1 & 9 \\ 3 & 0 & 1\end{bmatrix}$$
問題4
定数係数2階線形微分方程式の問題です
解き方を知らない方はこちらの記事を閲覧をおすすめします
今回の解き方も記事通りに進めています
ぜひ参考にしてください
(1)与式の特性方程式は$${\lambda}^2 + 1 = 0$$$${\lambda} = \pm i$$
よって基本解u1 , u2はそれぞれ$$u_{1} = \cos{x}, u_{2} = \sin{x}$$
よって一般解はC1 , C2を任意定数として$$u_{c} = C_{1}\cos{x} + C_{2}\sin{x}$$
(2)基本解u1、u2のロンスキアン(ロンスキー行列式)W(u1,u2)は
$$\begin{align*}
W(u_1,u_2)
&=\begin{vmatrix} u_1 & u_2 \\ u_{1}' & u_{2}'\\\end{vmatrix}\\
&=\begin{vmatrix} \cos{x} & \sin{x} \\ -\sin{x} & \cos{x}\\\end{vmatrix}\\
&=\cos^2 x + \sin^2 x = 1
\end{align*}$$
ここで基本解u1,u2がわかっているとき特殊解upは、cosx = R(x)とすると
u_{p}
&= -u_{1}\int_{}^{}{\frac{u_2 R(x)}{W(u_1,u_2)}}dx + u_{2}\int_{}^{}{\frac{u_1 R(x)}{W(u_1,u_2)}}dx \\
&= -\cos{x}\int_{}^{}{\sin{x}\cos{x}}dx + \sin{x}\int_{}^{}{\cos{x}\cos{x}}dx\\
&= -\cos{x}(-\frac{1}{2}\cos^2 x) + \sin{x}\frac{x + \cos{x} \sin{x}}{2}\\
&= \frac{1}{2}(\cos^3 x + \sin^2 x \cos{x} +x\sin{x})\\
&= \frac{1}{2}(\cos{x} + x\sin{x})
\end{align*}$$
よって一般解は
(3)
(1) , (2)の結果より$$u = u_{c} + u_{p}$$を変形して
u_{p}
&= u - u_{c}\\
&= C_{1}' \cos{x} + C_{2}\sin{x} + \frac{1}{2}x\sin{x} - C_{1}\cos{x} + C_{2}\sin{x}\\
&= \frac{1}{2}(\cos{x} + x\sin{x})
\end{align*}$$
【別解】
(2)より$$\frac{1}{2}(\cos{x} + x\sin{x})$$