8.1
重心の移動を考える。
重心の位置は横倒しのときは0.15[m]、直立のときは2.5[m]
よって
8.2
質量500[kg]の物体とロープに分けて考えると
8.3
自然長をXとする。重りと伸びの比率より
$$200:(10 - X) = 350:(13 - X)$$
$$X = 0.06[m]$$
F = kxより$$0.2 * 9.8 = k * 0.04$$
$$k = 49[N/m]$$
10[cm]にするためのエネルギーW_1は
15[cm]にするためのエネルギーW_2は
よって必要なエネルギーEは$$E = W_2 - W_1 = 1.6*10^{-1}[J]$$
8.4
8.5
失ったエネルギーEは「最初の位置エネルギー」-「床に達したときの運動エネルギー」であるから
8.6
「最初の位置エネルギー」=「10[cm]縮んだときの弾性エネルギー」より、自然長からの高さをxとすると$$Mgh = \frac{1}{2}kx^2$$$$3*9.8*(x+0.1) = \frac{1}{2}*2000*0.1^2$$$$x = 0.24[m]$$
8.7
8.6と同様に考えて$$\frac{1}{2}kx^2 = Mgh$$$$\frac{1}{2}*3000*0.1^2 = 0.03*9.8*h$$$$h = 51[m]$$
8.8
急に手を離したときはエネルギー保存則が成り立つから$$Mgx = \frac{1}{2}kx^2$$$$x = \frac{2Mg}{k}$$
静かに手を離したときは力のつり合いが成り立つから$$kx = Mg$$$$x = \frac{Mg}{k}$$
8.9
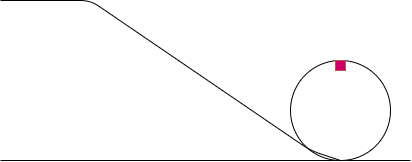
落ちることなく1回転させるためには図の赤の位置で「遠心力」≧「重量」が成り立てばよい。
赤の部分の速度はエネルギー保存則より$$Mgh = 2Mgr + \frac{1}{2}Mv^2$$$$v = \sqrt{2g(h-2r)}$$
$$Mg ≦ M\frac{v^2}{r} ≦ M\frac{2g(h-2r)}{r}$$
$$h≧\frac{5}{2}r$$
8.10
木の抵抗力をF、弾丸の質量をmとすると$$\frac{1}{2}mv^2 = Fx$$$$F = 25*100^2m$$これを$$\frac{1}{2}*250^2m = Fx$$に代入して$$x = 0.125[m]$$
8.11
5[kg]、3[kg]の球の衝突後の速さをそれぞれv_1'、v_2'とする。
運動量保存則とはねかえり係数より$$mv = mv'$$$$5*8+3*5 = 5v_1' + 3v_2'$$$$55 = 5v_1' + 3v_2'$$$$e = -\frac{v_1' - v_2'}{8-5}$$$$-1.8 = v_1' - v_2'$$よって$$v_1' = 6.2[m/s] , v_2' = 8.0[m/s]$$
損失したエネルギーEは
E
&= \frac{1}{2}mv^2 - \frac{1}{2}mv'^2\\
&=\frac{1}{2}{5*8^2 + 3*5^2 - \frac{1}{2}(5*6.2^2+3*8^2)} \\
&= 5.4[J]
\end{align*}$$
8.12
1000[mm^3]は1[kg]であるから、1000[m^3]は1*10^6[kg]、よって
8.13
1馬力(PS) ≒ 735[W]より
8.14
$$P = \frac{3*10^3*20}{60} = 1000[W]$$
8.15
8.16
勾配を持たないとき$$F_1 = 2*10^5*\frac{100}{1000} = 2*10^4[N]$$1/1000の勾配を持つときこれに
が加わるからP = Fvより
$$v = 36.4[m/s]$$
8.17
8.18
モータの半径を1[m]として考える。
350[N*m]/1[m] = 350[N]
3000[rpm] = 3000*2π/60[m/s]より
$$P = Fv = 1.1*10^5[W]$$
以上です。
間違い、質問などありましたらコメントよろしくお願いします。
