ばね定数が異なるばねを連結させたとき、それらを1つのものとして考えたばね定数を合成ばね定数といい、つなぎ方によって値が変わります
そしてその値は次の式で表されます
$$\begin{align*}&直列~:~\frac{1}{k} = \frac{1}{k_{1}} + \frac{1}{k_{2}} \\ &並列~:~k = k_{1} + k_{2} \\ &サンドイッチ~:~k = k_{1} + k_{2}\end{align*}$$

教科書や参考書にも公式が載っていたりしますが、こう思ったことはありませんか

もちろんこのまま暗記しても良いのですが、導出方法を知っていた方が応用問題などにも対応できます
ですので、今回はこの3つの式の導出方法を解説していきたいと思います
ぜひ最後までご覧ください
前提知識
ばねを引っ張ると、ばねは縮もうとします。反対にばねを縮めようと力を加えると、ばねは伸びようとします
このような力を弾性力といいます
そして、弾性力の大きさFは、ばねの伸び縮みの長さxに比例します。これをフックの法則といい、次式で表します
$$F = kx$$
このときの比例定数kをばね定数といいます
直列接続
まずは、直列接続からやっていきます
ばねを力Fで引っ張ると、自然長からxだけ伸びるとします

このk1とk2が組み合わさったばね定数をkとすると、これが合成ばね定数であり、フックの法則より$$F = kx \cdots ①$$が成り立ちます
この状態では、それぞれのばねには以下の図のように力が加わっています
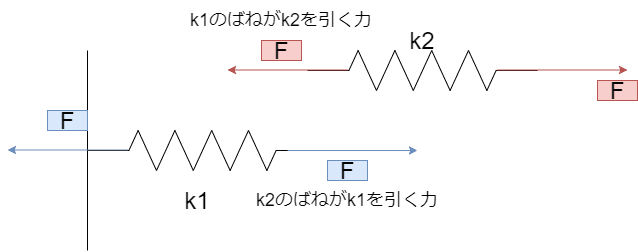
k2のばねが右から引っ張られているときに、k2のばねは静止しているので、k2のばねの左側にも同じ力Fがはたらきます
そして、作用反作用の法則でk1のばねにも力Fがはたらきます。k1のばねも静止しているので、k1のばねの左側にも同じ力Fがはたらきます
ここで、それぞれのばね定数は異なるので、それぞれのばねの伸びが異なることを考え、k1とk2のばねの伸びをそれぞれx1 , x2とおいて、次の図を考えます
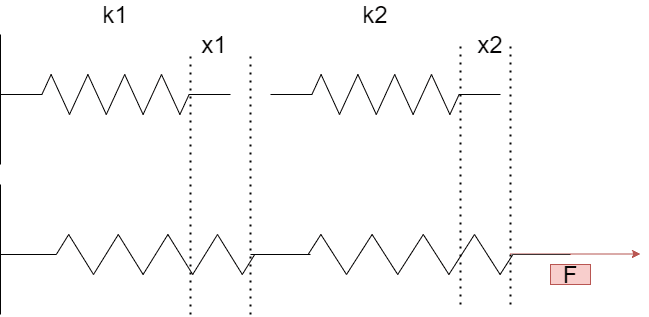
k1のばねにも、k2のばねにも同じ力Fが働くので、フックの法則より$$F = k_{1}x_{1} ~~ F=k_{2}x_{2}$$となる
変形すると$$x_{1} = \frac{F}{k_{1}} ~,~x_{2} = \frac{F}{k_{2}}$$となるので、これらを①に代入すると
$$F = k(\frac{F}{k_{1}} + \frac{F}{k_{2}})$$
$$\frac{1}{k} = \frac{1}{k_{1}} + \frac{1}{k_{2}}$$
となり、直列接続の合成ばね定数が求められました
並列接続
次に並列接続について考えます
ばねを力Fで引っ張ると、自然長からxだけ伸びるとします

このとき、k1 , k2それぞれのばね定数が異なるので、それぞれのばねにかかる力が異なります
ですので、その力をそれぞれF1 , F2というようにおいています
力の関係とフックの法則より$$F = F_{1} + F_{2}~,~F_{1} = k_{1}x~,~F_{2} = k_{2}x$$
これらより$$F = k_{1}x + k_{2}x = (k_{1} + k_{2})x$$となるから、フックの法則より
$$k = k_{1} + k_{2}$$
となり、並列接続の合成ばね定数が求められました
サンドイッチ
ばねを力Fで引っ張ると、自然長からxだけ伸びるとします
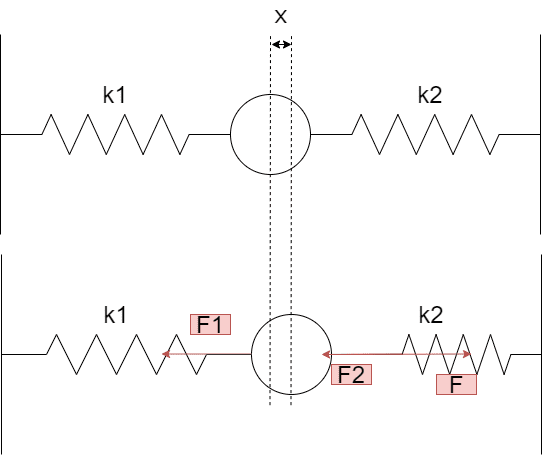
このとき、k1のばねはxだけ伸び、k2のばねはxだけ縮んでいます
k1 , k2のばねはそれぞれ、縮もうとする力F1、伸びようとする力F2が加えた力Fと反対方向に働くので、力のつり合いとフックの法則より
$$F = F_{1} + F_{2}~,~F_{1} = k_{1}x~,~F_{2} = k_{2}x$$
となるから
$$F = k_{1}x + k_{2}x$$となるため、フックの法則より
$$k = k_{1} + k_{2}$$
となり、サンドイッチ型の合成ばね定数が求められました
まとめ
今回は、合成ばね定数の導出方法について解説しました
公式をこのまま覚えている人も多いと思いますが、もし忘れてしまったときのために導出方法も知っておくと良いと思います