周波数解析法として、ボード線図やナイキスト線図、ベクトル軌跡があります
この記事では、ベクトル軌跡の書き方や意味について説明します
この記事で出てくる"ゲイン"や"周波数伝達関数"、"位相"について知らない場合は、まずこちらの記事からご覧ください
-
周波数伝達関数・周波数応答・周波数特性それぞれの意味を解説
続きを見る
ベクトル軌跡
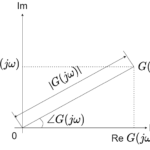
周波数伝達関数\(G(j\omega)\)は、角周波数\(\omega\)の値によって変化する複素数なので、大きさと偏角(位相)を持つベクトルとして複素平面上に記述できます
そして、角周波数\(\omega\)を0から∞まで変化させたときの周波数伝達関数\(G(j\omega)\)の軌跡をベクトル軌跡と呼びます
では、基本要素のベクトル軌跡を見ていきましょう
比例要素
比例要素の伝達関数は\(G(s) = K\)ですので、周波数伝達関数は\(G(j\omega) = K\)となります
定数\(K\)であるから、ベクトル軌跡は実軸上の\((K,0)\)の1点のみとなります
微分要素
微分要素の伝達関数は\(G(s) = sT\)ですので、周波数伝達関数は\(G(j\omega) = j\omega T\)となります
虚数であるため、常に虚軸上にあります
\(\omega = 0\)のとき、\(G(j\omega) = 0\)
\(\omega = \infty\)のとき、\(G(j\omega) = \infty\)
であるから、\(T=1\)としたベクトル軌跡は以下のようになります

積分要素
積分要素の伝達関数は\(G(s) = \frac{1}{sT}\)ですので、周波数伝達関数は\(G(j\omega) = -j\frac{1}{\omega T}\)となります
虚数であるため、常に虚軸上にあります
\(\omega = 0\)のとき、\(G(j\omega) = -\infty\)
\(\omega = \infty\)のとき、\(G(j\omega) = 0\)
であるから、\(T=1\)としたベクトル軌跡は以下のようになります

一次進み要素
一次進み要素の伝達関数は\(G(s) = 1+Ts\)ですので、周波数伝達関数は\(G(j\omega) = 1+j\omega T\)となります
微分要素に実数1が加わっただけのものと考えると、\(T=1\)としたベクトル軌跡は以下のようになります

微分要素と横軸を比べてみると1だけ移動していることが分かると思います
一次遅れ要素
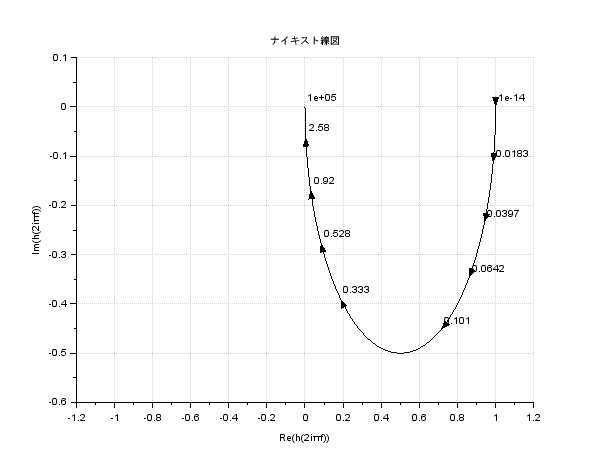
一次遅れ要素の伝達関数は\(G(s) = \frac{K}{1+Ts}\)ですので、周波数伝達関数は\(G(j\omega) = \frac{K}{1+j\omega T}\)となります
大きさ\(|G(j\omega)|\)は
$$|G(j\omega)| = \frac{K}{ \sqrt{(\omega T)^2 + 1}}$$
位相\(\phi\)は
$$\begin{align*}
\phi
&= \tan ^{-1}\frac{Im~G(j\omega )}{Re~G(j\omega )}\\
&= \tan ^{-1}\frac{0}{K} - \frac{\omega T}{1}\\
&= -\tan ^{-1}\omega T[deg]
\end{align*}$$
となります
\(\omega = 0\)のとき、\(|G(j\omega)| = K~,~\phi = 0[deg]\)
\(\omega = \frac{1}{T}\)のとき、\(|G(j\omega)| = \frac{K\sqrt{2}}{2}~,~\phi = -45[deg]\)
\(\omega = \infty\)のとき、\(|G(j\omega)| = 0~,~\phi = -90[deg]\)
であるから、\(T=1~,~K=1\)としたベクトル軌跡は以下のようになります
二次遅れ要素
二次遅れ要素の伝達関数は\(G(s) = \frac{K\omega _{n}^2}{s^2 + 2\zeta \omega _{n}s + \omega _{n}^2}\)であるから、周波数伝達関数は\(G(j\omega) =\frac{K\omega _{n}^2}{-\omega ^2 + \omega _{n}^2 + j2\zeta \omega _{n}\omega}\)となります
大きさ\(|G(j\omega)|\)は
$$|G(j\omega)| = \frac{K\omega _{n}^2}{\sqrt{(\omega _{n}^2 - \omega ^2)^2 + (2\zeta \omega _{n}\omega)^2}}$$
位相\(\phi\)は
$$\begin{align*}
\phi
&= \tan ^{-1}\frac{Im~G(j\omega )}{Re~G(j\omega )}\\
&= \tan ^{-1}\frac{0}{K\omega _{n}^2} - \tan ^{-1}(\frac{2\zeta \omega _{n}\omega}{\omega _{n}^2 - \omega ^2})\\
&= -\tan ^{-1}(\frac{2\zeta \omega _{n}\omega}{\omega _{n}^2 - \omega ^2})[deg]
\end{align*}$$
となります
\(\omega = 0\)のとき、\(|G(j\omega)| = K~,~\phi = 0[deg]\)
\(\omega = \infty\)のとき、\(|G(j\omega)| = 0~,~\phi = -180[deg]\)
\(T=1~,~\omega _{n}=1\)としたベクトル軌跡は以下のようになります
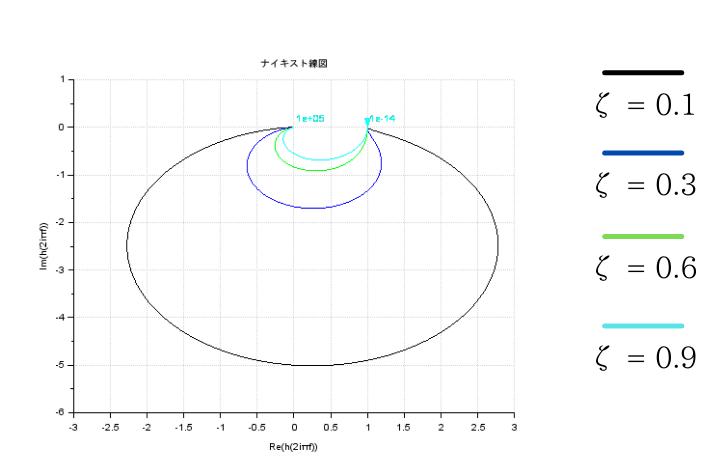
二次遅れ系のベクトル軌跡の軌道は、他の要素のものとは違ってシンプルに描けるものではありません
\(\omega\)の値を代入して、計算の結果からプロットをしていくしかありません
むだ時間要素
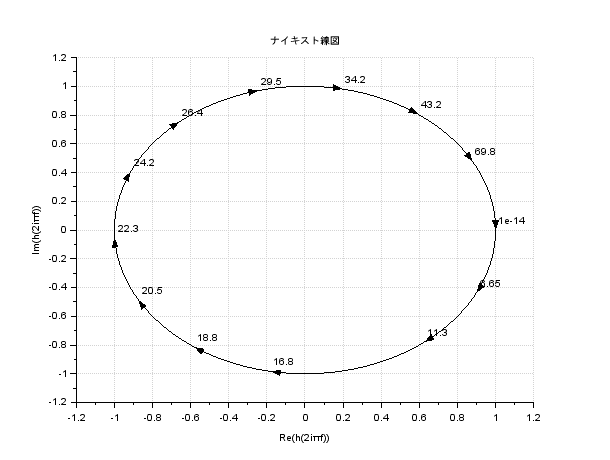
むだ時間要素の伝達関数は\(G(s) = e^{-\tau s}\)ですので、周波数伝達関数は\(G(j\omega) = e^{-j\omega\tau}\)となります
オイラーの公式より\(e^{-j\omega\tau}= \cos {\omega \tau} - j\sin {\omega \tau}\)であるから
大きさ\(|G(j\omega)|\)は
$$|G(j\omega)| = 1$$
位相\(\phi\)は
$$\begin{align*}
\phi
&= \tan ^{-1}\frac{Im~G(j\omega )}{Re~G(j\omega )}\\
&= \tan ^{-1}\frac{-\sin {\omega \tau}}{\cos {\omega \tau}}\\
&= -\tan ^{-1}\tan {\omega \tau}\\
&= -\omega \tau
\end{align*}$$
となります
大きさは常に1であるから、単位円上を移動します
位相は
\(\omega = 0\)のとき、\(\phi = 0[deg]\)
\(\omega = \infty\)のとき、\(\phi = -\infty[deg]\)
であるから、ベクトル軌跡は以下のようになります
まとめ
この記事では、ベクトル軌跡の意味や描き方について説明しました
ベクトル軌跡は、周波数解析法の一つとして大学院試験にもよく出題されるのでぜひ覚えておいてください
Scilab
今回のベクトル軌跡は「Scilab」というMATLABに似たソフトを使って作成しました
Scilabは無料ソフトで、MATLABよりも軽いので非常に使いやすいです
実際に書いて試してみたい方は、ぜひ使ってみてください