偏心衝突についての記事です
向心衝突と異なり、回転まで考えなければならない少し複雑なものですが、換算質量・打撃の中心について式を丁寧に解説していきます
偏心衝突とは
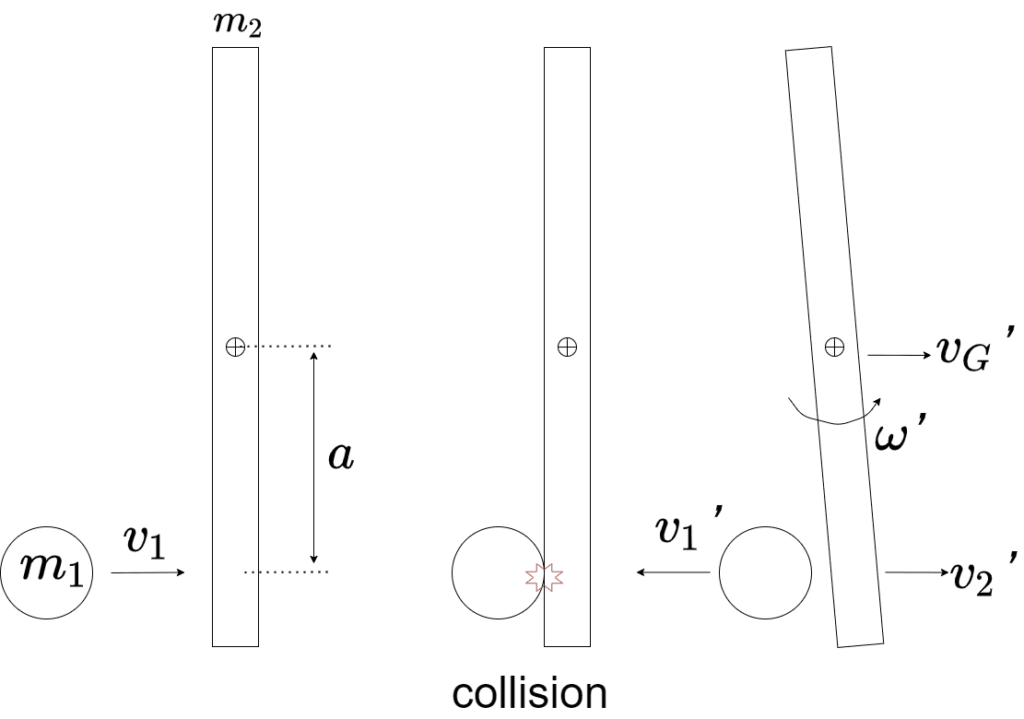
上の図のように、物体が衝突するとき、力の作用線が両方の物体の重心を通らないとき、この衝突を偏心衝突といいます
通常の衝突、力の作用線が重心を通るときと比べて回転運動も考えなくてはならないので、少し計算が複雑になります
換算質量mredを導出する
まず、反発係数eは
$$e = -\frac{v_{1}' - v_{2}'}{v_{1}'}\cdots①$$
となります
\(v_{G}'\)ではなく、\(v_{2}'\)となっているのは、衝突点での反発係数であるからです
次に、運動量保存と角運動量保存の式は
$$m_{1}v_{1} = m_{1}v_{1}' + m_{2}v_{G}'\cdots②$$
$$m_{1}av_{1} = m_{1}av_{1}' + I_{G}\omega '\cdots③$$
となります
運動量保存と角運動量保存の式は、重心の運動についてなので、\(v_{G}'\)となっています
また、\(I_{G}\)は棒の重心まわりの慣性モーメントです
さらに、\(v_{2}'\)と\(v_{G}'\)の関係を考えます
v_{2}'の速度は、「重心の速度+角速度×重心から衝突点までの距離」で表せるから
$$v_{2}' = v_{G}' + a\omega '\cdots④$$
となります
これらを変形していきます
②より
$$\begin{align*}m_{2}v_{G}' &= m_{1}v_{1}-m_{1}v_{1}'\\
v_{G}' &= \frac{m_{1}}{m_{2}}(v_{1} - v_{1}')\cdots⑤
\end{align*}$$
③より
$$\omega '= \frac{m_{1}a}{I_{G}}(v_{1} - v_{1}')\cdots⑥$$
⑤、⑥を④に代入すると
$$\begin{align*}
v_{2}'
&= \frac{m_{1}}{m_{2}}(v_{1} - v_{1}') + \frac{m_{1}a^2}{I_{G}}()v_{1} - v_{1}'\\
&= (\frac{1}{m_{2}} + \frac{a^2}{I_{G}})m_{1}(v_{1} - v_{1}')\cdots⑦
\end{align*}$$
となります
②、⑦より
$$\begin{align*}
v_{2}' &= (\frac{1}{m_{2}} + \frac{a^2}{I_{G}})m_{2}v_{G}'\\
m_{2}v_{G}' &= \frac{1}{\frac{1}{m_{2}}+\frac{a^2}{I_{G}}}v_{2}'\\
&= \frac{m_{2}}{1+\frac{m_{2}a^2}{I_{G}}}v_{2}'\\
&= \frac{m_{2}}{1+\frac{a^2}{k_{G}^2}}v_{2}'\cdots ⑧
\end{align*}$$
となります
\(k_{G}\)は回転半径で、\(I_{G} = m_{2}k_{G}^2\)です
ここで、\(\frac{m_{2}}{1+\frac{a^2}{k_{G}^2}}\)を\(m_{red}\)とおくと、②、⑧より
$$m_{1}v_{1} = m_{1}v_{1}' + m_{red}v_{2}'\cdots ⑨$$
となります
この式は、質量\(m_{1}\)の物体が、\(m_{red}\)の物体に向心衝突(力の作用線が物体の重心上にある場合の衝突)をしたときの運動量保存の式と同じ形になります
この\(m_{red}\)を換算質量(reduced mass)と言います
換算質量を使うことで、向心衝突と同じような方法で衝突後の\(v_{1}'\)と\(v_{2}'\)を求めることができます
ちなみに①、⑨より\(v_{1}'\)と\(v_{2}'\)は
$$v_{1}' = \frac{m_{1} - em_{red}}{m_{1} + m_{red}}v_{1}~~~~v_{2}' = \frac{m_{1}(1+e)}{m_{1} + m_{red}}v_{1}$$
となります
打撃の中心
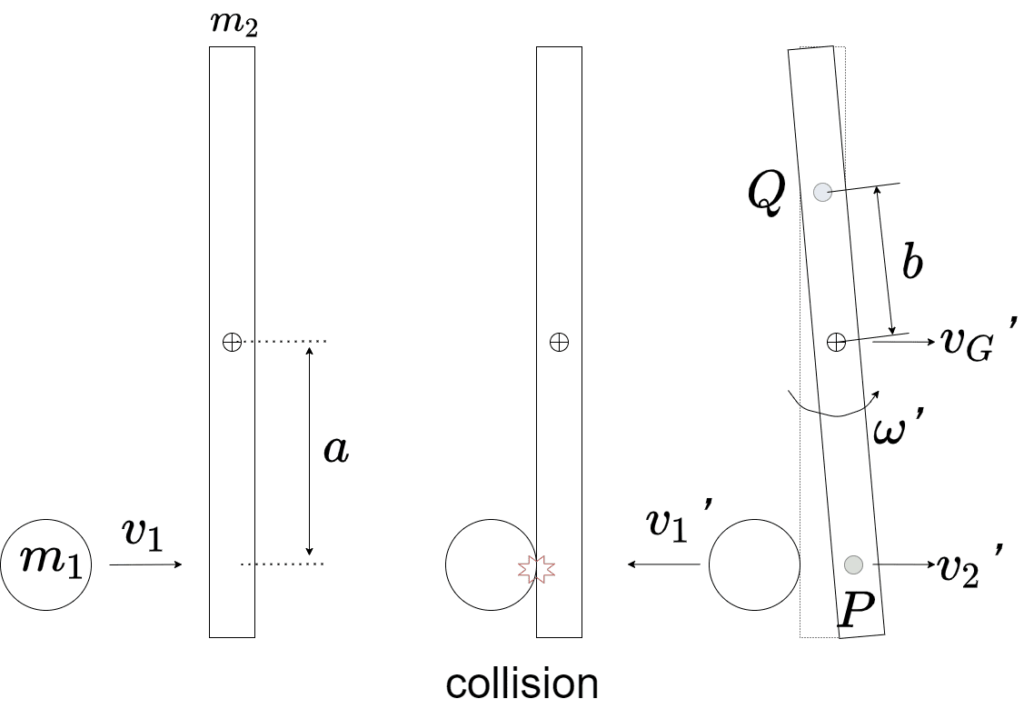
偏心衝突して、棒が回転したときに動かない点が一つあります
上の図であれば、点Q(青色の点)の部分が動いていません
この動かない点Qは点Pに対して打撃の中心と言います
重心までの距離をbとして、bについて考えます
点Qの速度は、先ほどの\(v_{2}'\)と同様に考えると\(v_{G}' - b\omega '\)となります
点Qは動いていないので
$$\begin{align*}
v_{G}' - b\omega ' &= 0\\
b &= \frac{v_{G}'}{\omega '}\cdots ⑩
\end{align*}$$
となります
⑤、⑥より\(\omega = \frac{a}{I_{G}}m_{2}v_{G}'\)であるから⑩は
$$\begin{align*}
b
&= \frac{v_{G}'}{\frac{a}{I_{G}}m_{2}v_{G}}\\
&= \frac{I_{G}}{m_{2}a}\\
&= \frac{k_{G}^2}{a}\\
ab &= k_{G}^2
\end{align*}$$
のようになります
これが打撃の中心の関係式になります
打撃の中心点P,Qは可逆的であり、点Pは点Qに対する打撃の中心であるとともに、点Qは点Pの打撃の中心となります
野球でバッターがホームランを打った時に「感触がなかった」のような事を言いますが、あれは打撃の中心を持って打ったからだと考えられます
点Qでバットを握って点Pでボールを打つときは、手に衝撃力は感じません