材料力学の内容で、理解できない人が多い「モールの応力円」について解説します。
モールの応力円とは
モールの応力円は、平面応力状態において、物体内部の任意面に作用する垂直応力と、せん断応力の関係を示す円の方程式のことです。
モールの応力円を使うことにより、外部の力によって内部にどのような力が生じているかを理解することができます。
例えば下図のように、中実丸棒を引っ張ったとき、どのように壊れるかがわかるようになります。

最大主応力説では下図のように

最大せん断応力説では下図のように壊れます。

モールの応力円の導出
2軸引張とせん断応力が加わった状態において考えます。
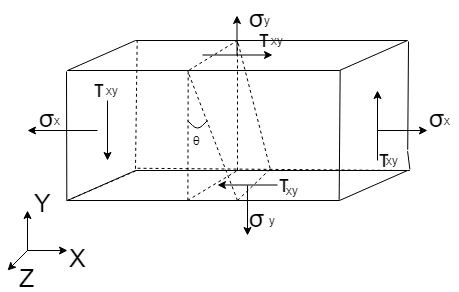
薄い部材の場合、Z軸に垂直な面の応力は生じないので
$$σ_z = τ_{xz} = τ_{zx} = τ_{zx}= τ_{xz} = 0$$
であり、この状態を「平面応力状態」といいます。
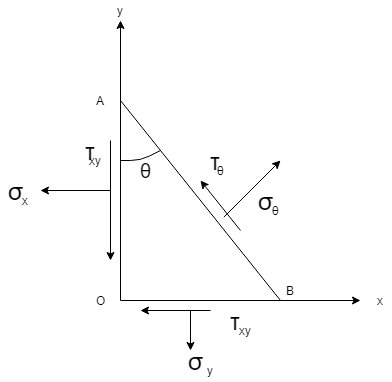
ここで、上の図の点線で示した、xy平面の三角形の力のつり合いを考えます。
傾斜面に生じる垂直応力と、せん断応力をそれぞれσθ、τθとします。
面ABの面積をSとすると、面AOの面積は(Scosθ)、面BOの面積は(Ssinθ)であるから、三角形OABのx方向とy方向の力のつり合いより
①、②を整理すると
ここで
より③、➃は
となる。⑤、⑥を整理すると
となります。⑦式はσ-τ座標系における、
これをモールの応力円といいます。
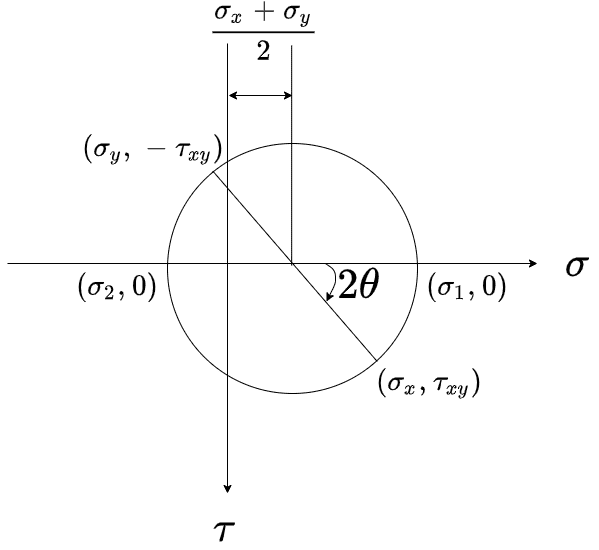
主応力と主せん断応力
知っている方もいると思いますが、一応解説しておきます。
③式、➃式で示したように、傾斜面に生じる垂直応力とせん断応力は、角度の関数となっています。
なので、せん断応力τが0となるような角度が存在し、このとき垂直応力σは最大または最小となります。このような垂直応力を「主応力」と言い、モールの応力円ではσ1,σ2が主応力を示しています。そしてこのような面を「主応力面」と言います。
また、垂直応力σが0となるような角度も存在し、このときのせん断応力τは最大または最小となります。このようなせん断応力を「主せん断応力」と言い、モールの応力円では、τ1,τ2が主せん断応力を示しています。そして、このような面を「主せん断応力面」と言います。
モールの応力円の使用法
モールの応力円から「主応力の値」、「主応力面の角度」、「主せん断応力の値」、「主せん断応力面の角度」を読み取ることができます。次の練習問題を解いてみましょう。
【練習問題】
以下のような応力状態のとき、モールの応力円を描き、主応力の値σmax、σmin、主応力面の角度θσmax、θσmin、主せん断応力の値τmax、τmin、主せん断応力面の角度θτmax、θτminをそれぞれ求めなさい。
【解答】
⑦式に代入すると
$$(σ_{θ} - 30)^2 + τ_{θ}^2 = 200$$
となり、中心(30,0)、半径14.14の円を表しています。
よってモールの応力円は以下のようになり、図より主応力は30+14.14 = 44.14[MPa]、30-14.14 = 15.86[Mpa]、σmaxの働く面は0°と180°、σminの働く面は90°と270°、主せん断応力は14.14[Mpa]、-14.14[MPa]、θτmaxの働く面は45°と225°、θτminの働く面は135°と315°になります。
(モールの応力円のグラフ上では2θなので、実際の面の角度は2で割った値です。つまり、モール応力円上を360°進めば元の位置に戻るので、物理空間では面の法線が180°進めばその面では同じ応力が働きます。よって、それぞれの面に+180°した面にも同じ応力が働きます。)
