説明のために公式一覧のページと一部文字を変更しています
以下のような正方形の断面二次モーメントを求めます
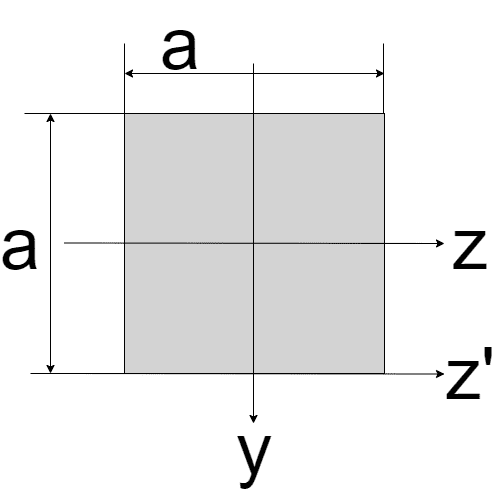
z軸からyだけ離れた微少長さdyを考える
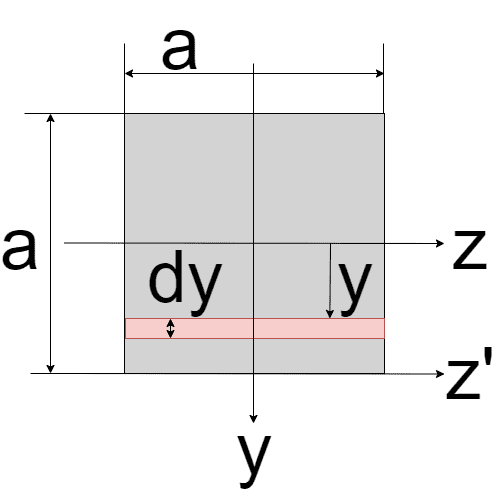
赤い微少部分の面積dAは
$$dA = ady$$
よって、z軸まわりの断面二次モーメントIzは
$$\begin{align*}
I_{z}
&= \int_{A}^{} y^2 a dy\\
&= a\int_{-\frac{a}{2}}^{\frac{a}{2}} y^2 dy\\
&= a\left[ \frac{y^3}{3} \right]_{-\frac{a}{2}}^{\frac{a}{2}}\\
&= \frac{a^4}{12}
\end{align*}
$$
図心から断面の端までの長さはa/2なので、断面係数は
$$Z_{z} = \frac{I_{z}}{\frac{a}{2}} = \frac{a^3}{6}$$
となる
面積をAとすると、z'軸まわりの断面二次モーメントは、平行軸の定理より
$$\begin{align*}
I_{z'}
&= I_{z} + A(\frac{a}{2})^2\\
&= \frac{a^4}{12} + \frac{a^4}{4}\\
&= \frac{a^4}{3}
\end{align*}$$
と求められる
断面の端までの長さはaなので、断面係数は
$$Z_{z'} = \frac{I_{z'}}{a} = \frac{a^3}{3}$$
となる