「アルハゼンの定理」についてです
アルハゼンの定理とは
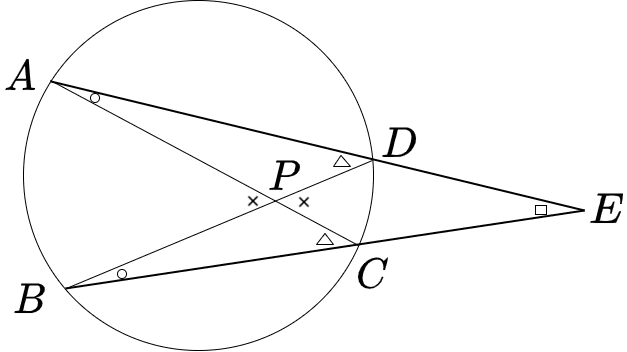
アルハゼンの定理は、上図のような図形における角度に関する定理です
アルハゼンの定理より
$$\angle APB = \angle ACB + \angle CBD \cdots ①$$
$$\angle AEB = \angle ACB - \angle CBD \cdots ②$$
が、成り立ちます
主に中学数学で、円が関係する図形の角度を求めるときに使えるものです
証明
証明はとても簡単です
まずは①の証明から
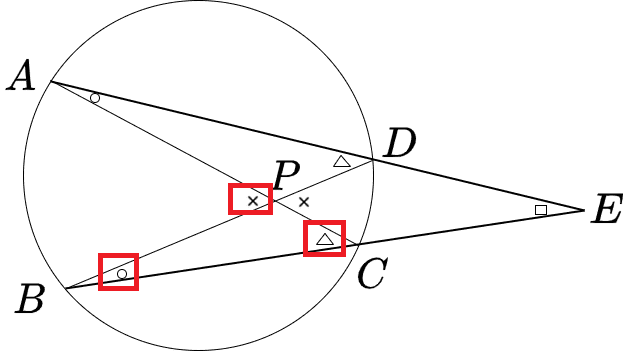
\(\triangle{BPC}\)に注目します
三角形の外角は、他の2つの内角の和に等しいから
$$\angle APB = \angle PCB + \angle CBP$$
となります
続いて②の証明
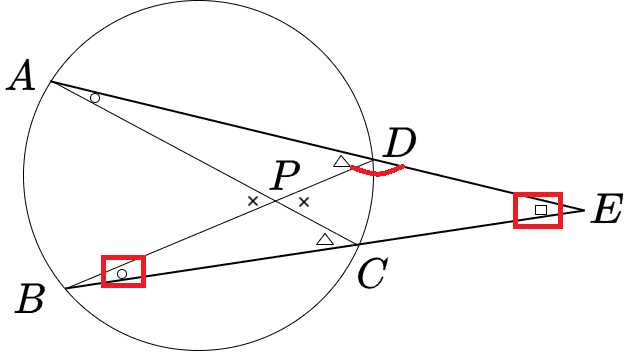
点Dにおいて
$$\angle BDE = 180 ^{\circ} - \angle ADP$$
次に、\(\triangle BDE\)に注目します
三角形の内角の和は180°であるから
$$\begin{align*}
\angle BED
&= 180^{\circ} - \angle BDE - \angle DBE\\
&= 180^{\circ} - (180 ^{\circ} - \angle ADP) - \angle DBE\\
&= \angle ADP - \angle DBE
\end{align*}$$
\angle BED
&= 180^{\circ} - \angle BDE - \angle DBE\\
&= 180^{\circ} - (180 ^{\circ} - \angle ADP) - \angle DBE\\
&= \angle ADP - \angle DBE
\end{align*}$$
となる
ここで
$$\angle ADP = \angle ACB ~,~\angle DBE = \angle CBD$$
であるから
$$\angle AEB = \angle ACB - \angle CBD$$
となります
