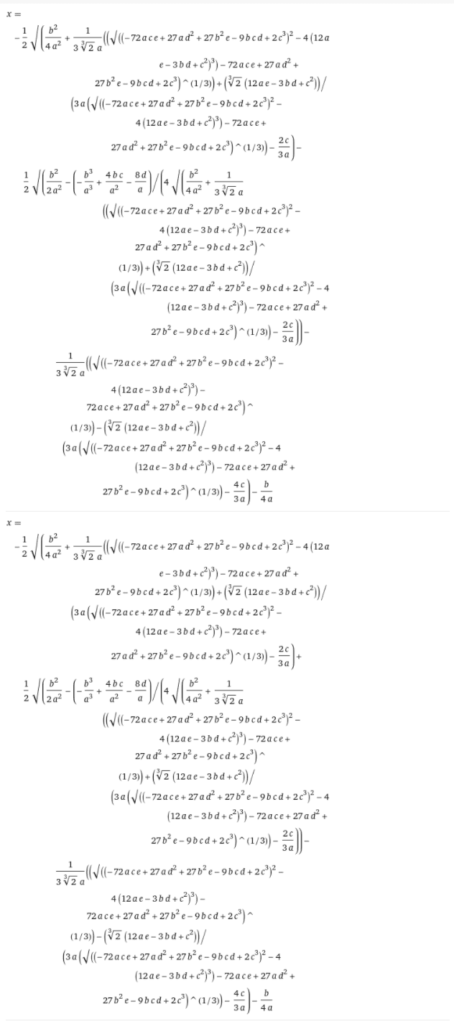皆さま大好き(?)二次方程式解の公式
$$x = \frac{-b\pm\sqrt{b^2 - 4ac}}{2a}$$
中学数学で覚えさせられたと思います
では、三次方程式の解は知っていますか?
実は三次方程式にも解の公式があり、証明もされています
今回は三次方程式の解の公式と、その導出方法を紹介します
三次方程式の解の公式
三次方程式$$ax^3 + bx^2 + cx + d = 0$$
の解の公式は下記のようになります

(引用:https://www.wolframalpha.com/input/?i=ax%5E3%2Bbx%5E2%2Bcx%2Bd%3D0&lang=ja)
とんでもない量の式ですが、解が3つであり、xがa,b,c,dのみで記述されていることがわかると思います
この公式は教科書には載っていませんね、もし載るとしたら式だけで何ページ使ってしまうのでしょうか…
ちなみにこの解の公式はWolfram Alphaという計算ソフトを使いました
Wolfram Alphaについての記事はこちらをご覧ください
三次方程式 解の公式の導出
ではいよいよ式の導出をしていきます
まずは$$x = X - \frac{b}{3a}$$とおいて
$$ax^3 + bx^2 + cx + d = 0$$に代入すると
$$a(X - \frac{b}{3a})^3 + b(X-\frac{b}{3a})^2+c(X-\frac{b}{3a}) + d = 0$$
それぞれ展開して
$$a(X^3 - \frac{b}{a}X^2+\frac{b^2}{3a^2}X - \frac{b^3}{27a^3}) + b(X^2 - \frac{2b}{3a}X + \frac{b^2}{9a^2})+c(X-\frac{b}{3a}) + d = 0$$
X^2は消去され
$$aX^3 + \frac{-b^2+3ac}{3a}X + \frac{2b^3-9abc+27a^2d}{27a^2} = 0$$
aで割って
$$X^3 + \frac{-b^2+3ac}{3a^2}X + \frac{2b^3-9abc+27a^{2}d}{27a^3} = 0…①$$
ここで
$$p = \frac{-b^2+3ac}{3a^2} , q = \frac{2b^3-9abc+27a^{2}d}{27a^3}$$
とおくと
①は$$X^3 + pX + q = 0…②$$となります
さらにここで$$X = u+v$$として、②に代入すると$$(u+v)^3 + p(u+v) + q = 0$$
整理すると
$$u^3 + v^3 + q + (3uv + p)(u + v) = 0…③$$
ここで$$u^3 + v^3 + q = 0 , 3uv + p = 0$$を満たすu , vが存在すれば、③を満たすことができる
変形をして
$$u^3 + v^3 = -q…④ , u^{3}v^{3} = -\frac{p^3}{27}…⑤$$
となり
二次方程式の和と積の関係よりu^3とv^3は対象であり
$$s^2 + qs - \frac{p^3}{27} = 0$$の解であることがわかる
よって、二次方程式の解の公式より
$$u^3 = \frac{-q+\sqrt{q^2+\frac{4p^3}{27}}}{2} , v^3 = \frac{-q-\sqrt{q^2+\frac{4p^3}{27}}}{2}$$
と求められる
これらの3乗根のうち$$uv = -\frac{p}{3}$$を満たす組を
$$u = \sqrt[3]{\frac{-q+\sqrt{q^2+\frac{4p^3}{27}}}{2}} , v = \sqrt[3]{\frac{-q-\sqrt{q^2+\frac{4p^3}{27}}}{2}}$$
と表すとu , vの組み合わせは
$$(u , v) = (\sqrt[3]{\frac{-q+\sqrt{q^2+\frac{4p^3}{27}}}{2}} , \sqrt[3]{\frac{-q-\sqrt{q^2+\frac{4p^3}{27}}}{2}})$$$$(\sqrt[3]{\frac{-q+\sqrt{q^2+\frac{4p^3}{27}}}{2}}\omega , \sqrt[3]{\frac{-q-\sqrt{q^2+\frac{4p^3}{27}}}{2}}\omega^2)$$$$(\sqrt[3]{\frac{-q+\sqrt{q^2+\frac{4p^3}{27}}}{2}}\omega^2 , \sqrt[3]{\frac{-q-\sqrt{q^2+\frac{4p^3}{27}}}{2}}\omega)$$
となる
よって解は
$$x=\begin{cases} \sqrt[3]{\frac{-q+\sqrt{q^2+\frac{4p^3}{27}}}{2}} + \sqrt[3]{\frac{-q-\sqrt{q^2+\frac{4p^3}{27}}}{2}} - \frac{b}{3a} \\ \sqrt[3]{\frac{-q+\sqrt{q^2+\frac{4p^3}{27}}}{2}}\omega + \sqrt[3]{\frac{-q-\sqrt{q^2+\frac{4p^3}{27}}}{2}}\omega^2 - \frac{b}{3a} \\ \sqrt[3]{\frac{-q+\sqrt{q^2+\frac{4p^3}{27}}}{2}}\omega^2 + \sqrt[3]{\frac{-q-\sqrt{q^2+\frac{4p^3}{27}}}{2}}\omega - \frac{b}{3a} \end{cases}$$
$$p = \frac{-b^2+3ac}{3a^2} , q = \frac{2b^3-9abc+27a^{2}d}{27a^3}$$
となります
p , qも代入した式が正しいのですが、式がぐちゃぐちゃになるのでこれで許してください
どうやったらこんな変形の仕方を思いつくのか、文字の置き方が難しすぎるなど、色々と声が聞こえてきそうですが、大体の流れが分かればいいと思います
おまけ:四次方程式の解の公式は?五次方程式は?
当然出てくる疑問だと思います
結論だけ言うと四次方程式の解の公式は存在し、それは以下のようになります
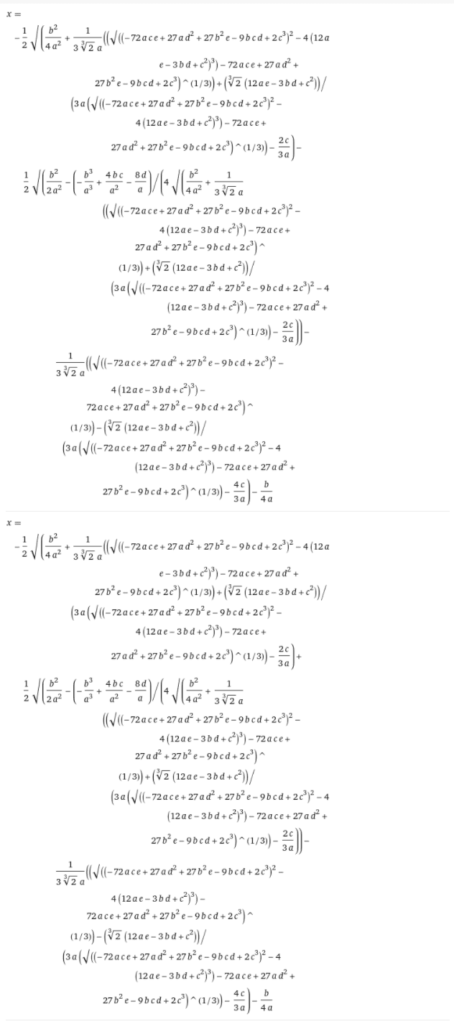

(引用:https://www.wolframalpha.com/input/?i=ax%5E4%2Bbx%5E3%2Bcx%5E2%2Bdx%2Be%3D0&lang=ja)
三次方程式を遥かに上回るとんでもない量の式が出てきました
ちなみに五次方程式以上の解の公式は存在しないことが証明されています
以上です、最後までお読みいただきありがとうございました
参考リンク:https://math-note.xyz/algebra/solutions-of-cubic-equation/