材料力学を学習中なら、聞いたことのある「弾性率」という言葉
ヤング率などと混ざって覚えてしまっている人もいると思いますが、実は ヤング率 = 弾性率 ではありません。ヤング率は弾性率の中の一つなのです
この記事では、弾性率について解説することで、ヤング率などとの違いについて理解できるように書いています
簡単に結論だけ知りたい人用
弾性率:「力/ひずみ」で求められる。力とひずみの関係を表す式
ヤング率:弾性率に含まれる、縦弾性係数のこと。「引張応力/ひずみ」で求められる。ヤング率が大きいということは、硬いということ
弾性率は3種類存在し、その中の一つがヤング率である
前提知識
力と伸びの関係 弾性
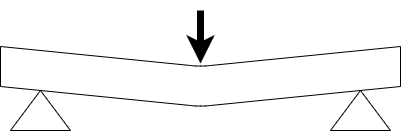
現実的には完全な剛体(決して変形しない物体)は存在しないため、物体に力を加えると、その物体は変形します
力を加えたときに、物体がどのように変化するかは、加えた力の大きさ、力を加えた位置、物体の厚さ、長さなど、様々な要素によって影響されます
・厚みが増すと変形が小さくなる
・加えた力が大きいと変形が大きくなる
・力と変形は一定の大きさまでは比例関係にある
などがあります
そして、力が加わると変形し、力を加えるのをやめると元に戻る性質を、「弾性」といいます
そしてその性質の限界点を「弾性限度」といいます
弾性限度を超えて力を加え続けると、力を加えるのをやめた後も変形が残ります
弾性体
弾性の性質を持つ物体のことを「弾性体」といいます
ゴムなどをイメージすると思いますが、鉄やコンクリートなども弾性体に含まれます
弾性率とは
前提知識で述べた通り、弾性体は力を加えると変化し、力を加えるのをやめると元に戻ります
力を加えているときの力とひずみの割合が「弾性率」です。「弾性係数」ともいいます
$$弾性率 = \frac{力}{ひずみ}$$
という式で表されます
弾性率には「ヤング率(縦弾性係数)」、「横弾性係数」、「体積弾性率」の3種類存在しています
順に解説していきます
ヤング率(縦弾性係数)
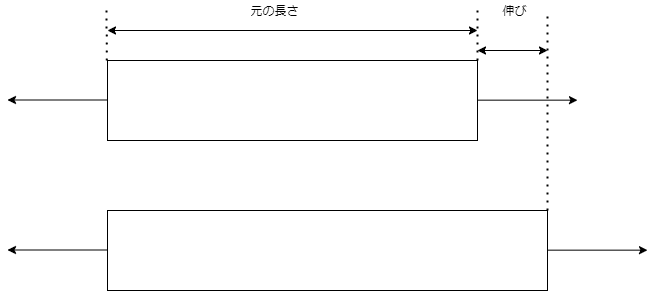
物体に力が加わり、物体の長さが伸びたとき$$ヤング率 = \frac{\frac{加えた力}{断面積}}{\frac{伸び}{元の長さ}}$$で表されます
材料力学では、ヤング率 , 応力 , ひずみをそれぞれ、E , σ , εとして$$E = \frac{\sigma}{\varepsilon}$$と表します
ヤング率が大きいほど、その物体は変形しにくいです
式からも分かりますね
ヤング率が大きいということは、固いということですね
横弾性係数

せん断弾性係数ともいいます
縦弾性係数の垂直応力と垂直ひずみを、せん断応力とせん断ひずみにしたものです
材料力学では、横弾性係数 , せん断応力 , せん断ひずみをそれぞれ、G , τ , γとして$$G = \frac{\tau}{\gamma}$$と表します
体積弾性率
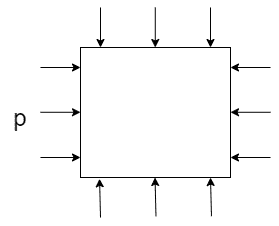
圧力pを受けて、体積が小さくなったとき、弾性率の関係から
のような式が成り立ちます
材料力学では、体積弾性率、体積ひずみをそれぞれ、K , εvとして$$K = \frac{p}{\varepsilon}$$と表します
弾性率と合わせて覚えておきたいもの
ポアソン比
物体に力を加えたときの、横と縦の変化の割合を表します
例えば、丸棒に引張の力を加えたときには、力を加えた方向には伸びますが、力と垂直な方向は絞られて、径が縮むことは想像できると思います
このようなときの横ひずみと縦ひずみの比がポアソン比です
ポアソン比 , 横ひずみ , 縦ひずみをそれぞれ、ν , ε' , εとして$$\nu = -\frac{\varepsilon '}{\varepsilon}$$と表します
横弾性係数とヤング率とポアソン比の関係式
$$G = \frac{E}{2(1+\nu)}$$で表されます
この式より、独立な値は2つであることが分かります
例えば、νとGが分かったら、Eは求められます
まとめ
今回は弾性率について解説しました
弾性率は3つあり、ヤング率はその内の一つということや、他の弾性率についても少しでも理解してもらえたら幸いです
