慣性モーメントの導出：三角形板

以下のような三角形板について考えます

質量はm、密度をρとします

まずはz軸まわりの慣性モーメントについて考える

下図のように微少長さdy、z軸からdyまでの距離をyとおく

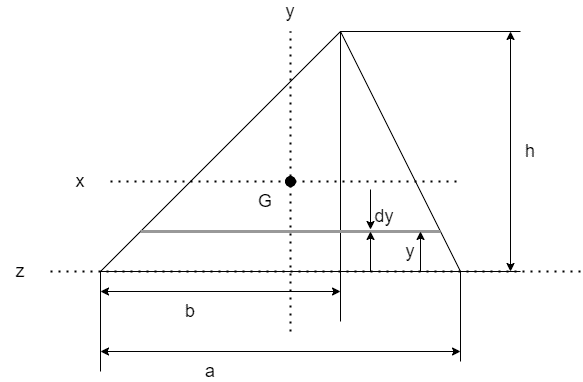
微少部分の質量dmは$$dm = \rho (a- \frac{a}{h}y)dy$$

密度は$$\rho = \frac{2m}{ah}$$よってz軸まわりの慣性モーメントは

$$\begin{align*}
I_{z}
&= \int_0^h \rho (a - \frac{a}{h}y) y^{2} dy\\
&= \frac{2m}{ah}\int_0^h (ay^2 - \frac{a}{h}y^3)dy\\
&= \frac{2m}{ah}\left[ \frac{a}{3}y^3 - \frac{a}{4h}y^4\right]_0^h\\
&= \frac{2m}{3}h^2 - \frac{m}{2}h^2\\
&= \frac{m}{6}h^2
\end{align*}$$

x軸まわりの慣性モーメントは、平行軸の定理より

次にy軸まわりの慣性モーメントを求めます

以下の図のように新たにy2軸をつくり、高さh、底辺の長さb , (a-b)それぞれの三角形に分けて考えます

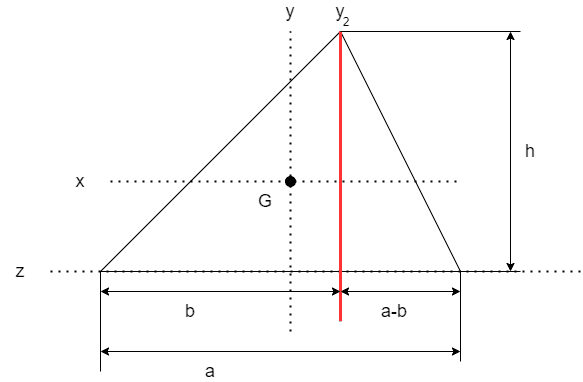
まずは左側の三角形について考えます

微少長さdx、dxまでの距離xとします

微少部分の質量dmは$$dm = \rho h (1 - \frac{x}{b})dx$$

よって左側の三角形の慣性モーメントは

$$\begin{align*}
I_{y_{2left}}
&= \int_{-b}^{0} \rho h(1 - \frac{x}{b})x^2 dx\\
&= \rho h\int_{-b}^{0} (x^2 - \frac{x^3}{b})dx\\
&= \rho h\left[ \frac{x^3}{3} - \frac{x^4}{4b} \right]_{-b}^{0}\\
&= \frac{1}{12}\rho h b^3
\end{align*}$$

同様に右側の三角形の慣性モーメントを求める

微少部分の面積は

$$dm = \rho \frac{hx}{a-b}dx$$

よって右側の三角形の慣性モーメントは

密度は$$\rho = \frac{2m}{ah}$$であるからy2軸の慣性モーメントは

$$\begin{align*}
I_{y_{2}}
&= I_{y_{2left}} +I_{y_{2right}}\\
&= \frac{1}{12}\rho h(a^3 - 3a^2 b + 3b^2)\\
&= \frac{1}{6}m(a^2 -3ab + 3b^2)
\end{align*}$$

y軸とy2軸の距離を求めます

下図のように、y2軸が通る頂点から重心Gを通って底辺に線を引きます

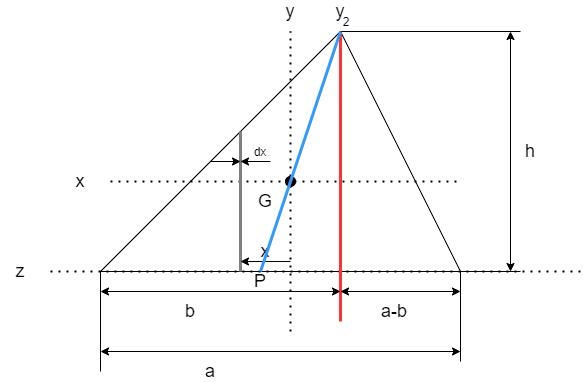
三角形の重心の高さは1/3の部分にあり、点Pはaを２等分するため

点Pからy2軸の距離は$$b - \frac{a}{2}$$

Gとy2軸の距離をlとすると

$$b-\frac{a}{2} : l = h : \frac{2h}{3}$$

$$l = \frac{2b-a}{3}$$

よってy軸まわりの慣性モーメントは、平行軸の定理より

重心Gを通り、この紙面に垂直な方向の軸まわりの慣性モーメントIは、直交軸の定理より

と求められる

回転半径は$$k = \sqrt{\frac{I}{m}}$$で求めることができる

これまでをまとめてみると

三角形板	慣性モーメント	回転半径
	$$I_{x} = \frac{mh^2}{18}$$	$$k_{x} = \frac{h}{3\sqrt{2}}$$
	$$I_{y} = \frac{m}{18}(a^2 - ab + b^2)$$	$$k_{y} = \frac{1}{3}\sqrt{\frac{a^2 - ab + b^2}{2}}$$
	$$I_{z} = \frac{m}{6}h^2$$	$$k_{z} = \frac{h}{\sqrt{6}}$$
	$$I = \frac{m}{18}(a^2 - ab + b^2 + h^2)$$	$$k = \frac{1}{3}\sqrt{\frac{a^2 - ab + b^2 + h^2}{2}}$$

となります

誤植、計算ミス等ありましたらコメントください

最後までお読みいただきありがとうございました

おもな物体の慣性モーメント一覧