6.1
$$I = 800*0.5^2 =200[kg*m^2]$$
6.2
6.3
※コメント欄に解答の詳細を載せています
直径20cmと15cmの球の質量と半径をそれぞれM , m , R , rとし、R/r = pとおく。
球の体積は$$\frac{4}{3}πr^3$$であるため$$M = (\frac{R}{r})^3m = p^3m$$これを$$4 = M - m$$に代入すると
よって慣性モーメントIは
またI = mk^2より$$k = \sqrt{\frac{I}{4}} = 7.3[cm]$$
6.4
左側から計5つの図形それぞれの慣性モーメントを求め、これらを足し合わせることで答えが出る。
まず、左端から順に質量を求めていく。
$$0.075^{2}π*0.2*7800 = 8.775π[kg]$$$$0.32*0.5*0.1*7800 = 124.8[kg]$$$$0.075^{2}π*0.15*7800 = \frac{26.325}{4}π[kg]$$$$0.32*0.5*0.1*7800 = 124.8[kg]$$$$0.075^{2}π*0.15*7800 = \frac{26.325}{4}π[kg]$$
慣性モーメントを左から順に求めていく、平行軸の定理より I = I_G + md^2、これを使用する。
これらを足し合わせると I = 12.9[kg*m^2]
6.5
20×3と12×3の長方形に分けて考える。
まず左下部分を(0,0)としたときの重心の座標(Gx , Gy)を求める。
よってx軸周り、y軸周りの断面二次モーメントをIx , Iyとすると
6.6
直径5cmの円柱と8cmの円柱それぞれの慣性モーメントを出し、それらを足し合わせる。
それぞれの慣性モーメント、質量をI1、I2、M1、M2 とし、求める位置が中心からxだけ右にあるとすると
これを微分して0になるxを求めると$$x = \frac{5*(M_2 - M_1)}{M_1+M_2} = 2.2[cm]$$
よって左端から12.2[cm]、重心は
$$G_x = \frac{5*5*π*10*5 + 8*8*π*10*15}{5*5*π*10 + 8*8*π*10} = 12.2[cm]$$
$$M_1 = 0.025*0.025*π*0.1*7800 = 1.531…[kg] , M_2 = 0.04*0.04*π*0.1*7800 = 3.92…[kg]$$
$$I_1 = \frac{1}{12}M_1*(3*0.025^2+0.1^2) = 0.00151…[kg*m^2] , I_2 = \frac{1}{12}M_2*0.1^2 = 0.00483…[kg*m^2]$$
よって
6.7
ω = 200[rpm]→200*2π/60[rad/s]
N = Iω'より$$I = 300*\frac{15*60}{200*2π} = 215[kg*m^2]$$
6.8
300[rpm]→300*2π/60[rad/s]
100[rpm]→100*2π/60[rad/s]
I = 300*0.5^2
6.9
100 = 60*ω'よりω' = 5/3
ω = ω0 + ω't = 16.7[rad/s] = 159[rpm]
6.10
ベルトA、Bの慣性モーメント、角加速度をそれぞれI_A , I_B , ω'_A , ω'_Bとする。
A,Bそれぞれのベルトの運動方程式を立てると$$T + T_{1}R_{A} - T_{2}R_{A} = I_{A}ω_{A}'$$$$T_{2}R_{B} - T_{1}R_{B} = I_{B}ω_{B}'$$
ベルトが滑らないので$$R_{A}ω_{A}' = R_{B}ω_{B}'$$
これらの式より
6.11
摩擦力をF'とする。
斜面方向の運動方程式と回転の運動方程式を立てると
また、a = rω'より
6.12
並進の運動方程式と回転の運動方程式を立てると
a = rω'より
よってF = -3F'ゆえに$$a = \frac{F-F'}{M} = \frac{4F}{3M}$$
6.13
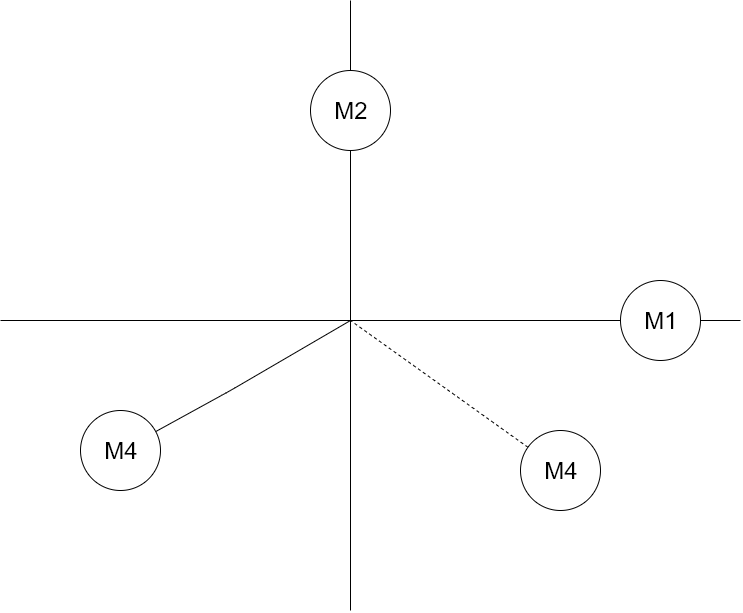
図のように考えて静的なつり合いを考えると
整理して
図から34.2[°]は成り立たない。
6章が終了して、やっと半分まで来ました。
残り半分も順に掲載していきますのでお待ちください。
間違い、質問等ありましたらコメントよろしくお願いします。
