モーメントは反時計回りを正とします。
上向き、右向きを正、下向き、左向きを負としています。
1.1
次のような図で考えます。
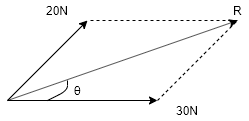
x方向の力の合力とy方向の力の合力をそれぞれRx,Ryすると
Rx = 30 + 20cos60° = 40[N]
Ry = 20cos30° = 17.32…[N]
よって合力Rと角度θは
となります。
1.2
分力をそれぞれF1,F2とするとx,y方向に関して次のような2つの式が成り立ちます。
これよりF2 = 51.8[N] , F1 = 73.2[N]となります。
1.3
x方向の合力とy方向の合力をそれぞれRx,Ryすると
よって合力Rと角度θは$$R = \sqrt{ R_{x}^2 + R_{y}^2 } = 123[N]$$
となります。
1.4
50N,80N,75N,60N,30Nの力をそれぞれF1~F5として任意の点O'をとってF1~F5をつなげて最後にO'からF5の先にベクトルF6を記述するとそのF6が合力となります。
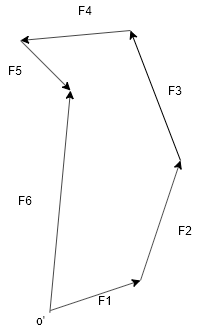
1.5
力をFi(i = 1,2,…,n)、任意の1点の位置ベクトルをrとするとモーメントはNi = r*Fiと表されます。
それらの和はΣNi = ΣrFi = rΣFiとなるので同一平面内で1点にはたらく多くの力の任意の点に関するモーメントの和はその合力のモーメントに等しいことがわかります。
1.6
50Nと60Nの力をx,y方向に分けて考えます。C点まわりのモーメントは
となります。
1.7
一番左側の点(左側のF1の始点)を基準点としてモーメントを考えると
となります。
1.8
-30*0.1=-3.0[N]
1.9
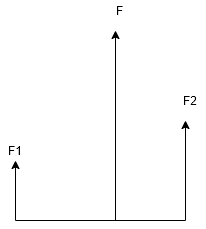
F1,F2の合力をFとするとF = F1 + F2 = 50[N]
またF1の始点を基準とすると合力の位置lは
となります。
1.10
F1が下向きとすると合力はF = F2 + F1 = 10[N]
またF1の始点を基準とすると合力の位置lは
※掲載されている答えはF2の始点からの距離なので答えは一致しています。
1.11
力をFi、角度をθi、x方向の力をFix、y方向の力をFiy、x,y座標をそれぞれXi,Yi、x,y方向の合力をそれぞれRx,Ryとして計算を表に整理すると
| Fi | θi | Fix | Fiy | Xi | Yi | FiyXi - FixYi |
| F1 = 8 | 315° | 8cos45° | -8sin45° | 0 | 0.15 | -0.8485… |
| F2 = 4 | 60° | 4sin30° | 4cos30° | 0 | 0 | 0 |
| F3 = 10 | 60° | 10cos60° | 10sin60° | 0.2 | 0 | √3 |
| F4 = 5 | 90° | 0 | 5 | 0.2 | 0.15 | 1 |
| Rx = 12.656… | Ry = 11.467… | N = 1.88 |
よって合力Rと角度θ、位置lは
となります。
1.12
x,y方向の合力をそれぞれRx,Ryとすると
よって合力Rと角度θは
点Aを基準としたモーメントNはN = -5sin45° * 0.1 -10sin60° * 0.2 + 4*0.3 = -0.8856…[Nm]
よって位置lは$$l = \frac{N}{R} = -0.199[m] = -19.9[cm]$$となります。
1.13
合力はR = -3-4+6-5 = -6[N]、合力の位置をlとして、モーメントのつり合いより左端(3Nのベクトル線上)を基準とすると$$-4*0.2 + 6*0.5 - 5*0.65 = Rl$$よりl = 0.175[m] = 17.5[cm]となります。
1.14
連力図と示力図を使って図式より求めます。こちらのサイトが参考になると思います。
http://www.eonet.ne.jp/~m-fujita/
1.15
1.14と同様のサイトで理解できると思います。
誤字、間違い、質問などありましたらコメントお願いします。
