以下のようにz軸からyだけ離れた微少範囲dyを考えます
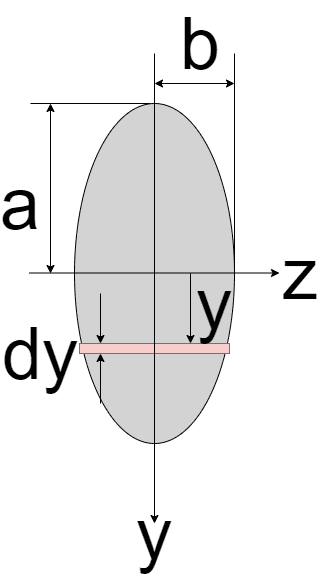
ここで、赤い微少部分の微少面積dAは近似的に長方形です
長方形の短辺はdyであり、長辺は高さによって異なります
楕円の方程式より
$$\begin{align*}
\frac{y^2}{a^2} + \frac{z^2}{b^2} = 1 \\
z^2 = b^2(1 - \frac{y^2}{a^2})\\
z = \frac{b}{a}\sqrt{a^2 - y^2}
\end{align*}$$
よって、赤い微少部分の面積dAは
$$dA = 2\cdot\frac{b}{a}\sqrt{a^2 - y^2}dy$$
となります
z軸まわりの断面二次モーメントは
$$\begin{align*}
I_{z}
&= \int_{A}^{} y^2 dA\\
&= 2 \cdot \int_{-a}^{a} y^2 \frac{b}{a} \sqrt{a^2 - y^2}dy\\
&= 2 \cdot \frac{b}{a} \int_{-a}^{a} y^2 \sqrt{a^2 - y^2}dy \cdot ①
\end{align*}$$
ここで、\(y = a\sin \theta\)であるから、\(dy = a\cos{\theta}d\theta\)が成り立つ
また、積分範囲は
| $$y$$ | $$-a$$ | $$\rightarrow$$ | $$a$$ |
| $$\theta$$ | $$-\frac{\pi}{2}$$ | $$\rightarrow$$ | $$\frac{\pi}{2}$$ |
であるから、①に代入して
$$\begin{align*}
I_{z}
&= \frac{2b}{a}\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} (a\sin{\theta})^2 \sqrt{a^2 (1 - \sin ^2 \theta)} a \cos{\theta}d\theta\\
&= 2a^3 b \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} (1 - \cos ^2 \theta)\cos ^2 \theta d\theta\\
&= 2a^3 b \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} (1 - \frac{1 + \cos{2\theta}}{2}) \cdot \frac{1 + \cos{2\theta}}{2} d\theta\\
&= 2a^3 b \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \frac{1 - \cos{2\theta}}{2} \cdot \frac{1 + \cos{2\theta}}{2} d\theta\\
&= \frac{a^3 b}{2} \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} (1 - \cos ^2 2\theta) d\theta\\
&= \frac{a^3 b}{2} \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} (1 - \frac{1+\cos{4\theta}}{2}) d\theta\\
&= \frac{a^3 b}{4} \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} (1 - \cos{4\theta}) d\theta\\
&= \frac{a^3 b}{4} \left[ \theta - \frac{\cos{4\theta}}{4} \right]_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\\
&= \frac{\pi a^3 b}{4}
\end{align*}$$
となり、断面二次モーメントが求められた
また、z軸から図の端までの長さはaであるから、断面係数は
$$Z = \frac{\frac{\pi a^3 b}{4}}{a} = \frac{\pi a^2 b}{4}$$
となる