5章ではほぼ全ての問題を運動方程式のみで解けます。
$$F = ma$$
5.1
F = ma = 60 * 19.6 = 1176[N]
5.2
重力加速度を考慮してF = m(a+g)より
300 = 10(a + 9.8)
a = 20.2[m/s]
5.3
0.01[s]で30[m/s]→0[m/s]となっているから加速度aは $$a = \frac{0-30}{0.01} = 3000[m/s^2]$$よって
$$F = ma = 3*3000 = 9000[N]$$
5.4
F = maより a = 3[m/s]
等加速度直線運動の3公式 の x = v_0t + 1/2at^2 より
$$200 = v_{0}*10 + 150$$よってv_0 = 5[m/s]
5.5
F = maよりa = 0.5[m/s^2]
等加速度直線運動の3公式 の v = v_0 + at より
$$v = 60*0.5 = 30[m/s]$$
5.6
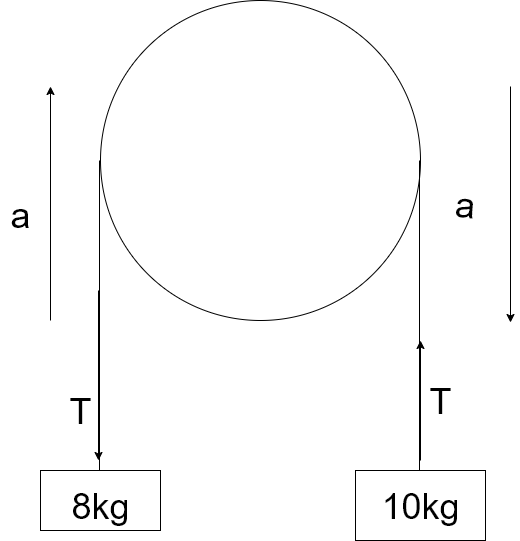
張力をTとし、8kgと10kgの重りそれぞれで運動方程式を立てると
$$10a = 10g - T , 8a = T - 8g$$これらよりa = 1.1[m/s^2] , T = 87[N]
5.7
ばねばかりの示す重さをM、物体の質量をmとして運動方程式を立てると$$m(1.5 + g) = Mg$$よってm = 8.7[kg]
5.8
下向きの加速度は重力加速度gであるため、10度傾いたときの横向きの加速度aは$$a = g*tan10° = 1.7[m/s]$$
※荷物の大きさ3kgは必要ない
5.9
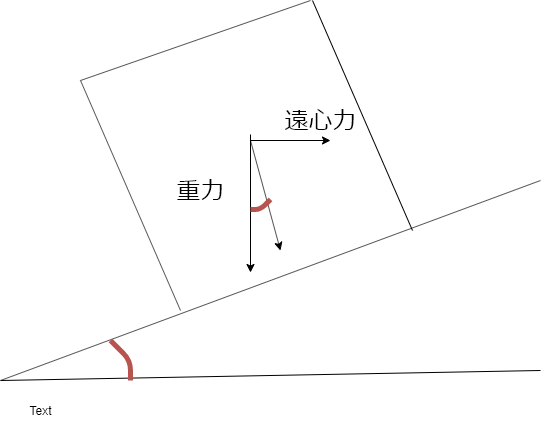
遠心力は$$Fr = \frac{mv^2}{r}$$よって上図の赤部の角度をθとすると$$tanθ = \frac{Fr}{mg} = \frac{v^2}{gr}$$よって$$θ = Arctan(\frac{v^2}{gr}) = 8.95°$$
二本のレールに等しい抗力を生じるためにはこの合力と垂直にレールを設置する必要がある。
よって必要な高さhはh = 1.435*sinθ = 0.233[m]
5.10
ω = 200[rpm]→20π/3[rad/s]
針金にかかる力は遠心力であるから
500Nまで耐えるとき$$500 = 2*1*ω^2$$よって
