この章は等加速度直線運動の3公式をよく使うので最初に記述しておきます。
$$v = v_{0} + at…①$$
$$v^2 - v_{0}^2 = 2ax…②$$
$$x = v_{0}t + \frac{1}{2}at^2…③$$
4.1
(a)$$10[m/s] = \frac{10*3600}{1000} = 36[km/h]$$
(b)
(c)$$20[rpm] = \frac{20*2π}{60} = 2.1[rad/s]$$
(d)
4.2
変位を時間tで微分すると速度、さらに微分すると加速度になる。
それぞれにt = 3[s]を代入すると答えがでる。
$$s = 5*3^3 - 20*9 + 8*3 - 3 = -24[m]$$
$$v = s' = 15t^2 - 40t + 8 = 23[m/s]$$
$$a = s'' = 30t - 40 = 50[m/s^2]$$
4.3
さきほどの問題を逆に考えて、速度を時間tで積分すると変位になる。
これにt = 5[s]を代入する。
$$\int_{}^{}{v}dt = \frac{5}{2}t^2 + 10t = 112.5[m]$$
4.4
まず単位を換算する。
等加速度であるから自動車の加速度は$$a = \frac{13.9}{10} = 1.39[m/s^2]$$進んだ距離は公式③より$$x = v_{0}t + \frac{1}{2}at^2$$初速度は0であるから$$x = \frac{1}{2}1.39*10^2 = 69.4[m]$$
4.5
公式②より$$v^2 - v_{0}^2 = 2ax$$$$1600 - 100 = 400a$$$$a = 3.75[m/s^2]$$
4.6
v-t線図の面積の部分が進んだ距離であるから
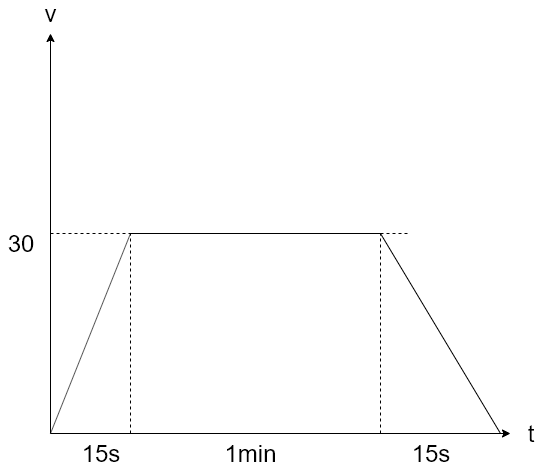
4.7
初速度は0であるから公式③より$$t = \sqrt{\frac{20}{g}} = 1.428… = 1.4[s]$$$$v = gt =9.8*1.4 = 14[m/s]$$
4.8
公式③より距離xは
また速さvは公式①より$$v = 9.8 + 9.8*5 = 58.8[m/s]$$
4.9
落下時間をt1、音の伝わる時間をt2、井戸の高さをy、音速をvとすると$$y= vt_{2}$$公式③より$$y = \frac{1}{2}gt_{1}^2$$$$t_{1} = \sqrt{\frac{2y}{g}}$$t1 + t2 = tとすると$$t = \sqrt{\frac{2y}{g}} + \frac{y}{v}$$$$(t - \frac{y}{v})^2 = \frac{2y}{g}$$$$y^2 - 2yv^2(\frac{t}{v} + \frac{1}{g}) + v^2t^2 = 0$$yについての2次方程式とみて
これらに数値を代入するとy = 10.6[m] , 24601[m]であり、解答として適切なのは10.6[m]となる。
4.10
気球が5[m/s]で上昇しているため、初速度5[m/s]の鉛直投げ上げ運動を考える。
高さh[m]の地点から石を落としたとすると公式③より$$y = 5*10 - \frac{1}{2}*9.8*10^2+h$$y = 0として整理すると$$h = 440[m]$$
4.11
(a)公式①より
(b)公式①より$$0 = 50sin30° - 9.8t$$$$t = \frac{50sin30°}{9.8} = 2.55[s]$$公式③より$$y = 50sin30° - \frac{1}{2}gt^2 = 31.9[m]$$
(c)問題(b)のtを2倍すればよいから
2.55*2 = 5.1[s]
(d)公式①より$$x = 5.1*50cos30° = 221[m]$$
4.12
これは45度になります。
計算過程など理由は別の記事で詳しく書きましたのでご覧ください
4.13
公式①より$$x = v_{0}cos45°t$$$$t = \frac{2000}{v_{0}cos45°}$$③より$$y = v_{0}sin45°t - \frac{1}{2}gt^2$$数値とtを代入して
整理して$$v = \sqrt{\frac{4.9*2000^2*2}{1800}} = 148[m]$$
4.14
4.2を変位→各変位、速度→角速度、加速度→各加速度に置き換えて考え、t = 5を代入すると角速度ωと各加速度ω'は$$ω = θ' = 9t^2 = 225[rad/s]$$$$ω' = θ'' = 18t = 90[rad/s^2]$$
4.15
回転数をnとすると角速度ωは$$ω = 2πn = 2π * \frac{45}{60} = 4.7[rad/s]$$周速度vは$$v = rω = 0.3*4.7 = 1.4[m/s]$$
4.16
60[rpm]→2π[rad/s]
300[rpm]→10π[rad/s]
角加速度ω'は
300rpmにおける周速度vは$$v = rω = 0.5 * 10π = 15.7[m/s]$$
公式③を変位→各変位、速度→角速度、加速度→各加速度に置き換えて考えると総回転角度θは
よって回転数は180
4.17
150rpm = \frac{2π*150}{60}[rad/s]
接戦加速度をat、法線加速度をanとすると$$a_{t} = rω' = 0.5*\frac{2π}{15} = 0.21[m/s^2]$$
4.18
列車A,Bの合計の長さは180[m]、これがすれ違うのに5秒かかっているから180/5 = 36[m/s]
また36[m/s]→129.6[km/h]であるから、求める列車Bの速さは129.6 - 50 = 79.6[km/h]
4.19
図よりQPに対して$$θ = tan^{-1}\frac{3}{4} = 36.9[°]$$大きさは5[m]

A,Bの変位はA(4t , 0) , B(10 , 3t)であるからABの距離Lは
よって最小となるのはt = 1.6[s]であり、その距離は$$L = \sqrt{36} = 6[m]$$
以上です。
間違い、質問等ありましたらコメントよろしくお願いします。
