下の図のような質量m、それぞれの辺の長さa , bの長方形板のx , y , zそれぞれの軸まわりの慣性モーメントを求めます
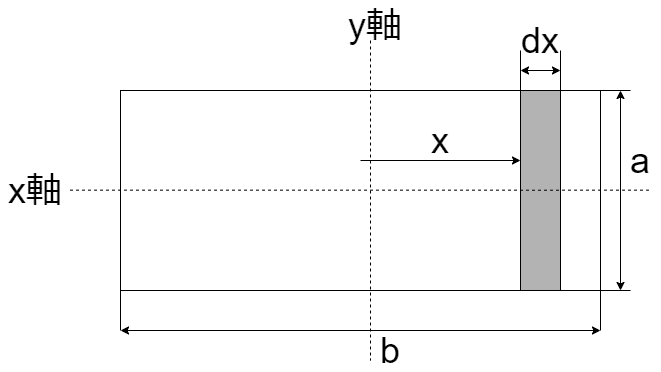
密度をρとするとx離れた微小部分dxの、y軸まわりの慣性モーメントは
$$I_{y} = \int_{-\frac{b}{2}}^{\frac{b}{2}} x^2 (\rho adx)$$
また$$\rho = \frac{m}{ab}$$より$$\rho adx = \frac{m}{b}dx$$であるから
$$\begin{align*}
I_{y}
&= \int_{-\frac{b}{2}}^{\frac{b}{2}} x^2 \rho adx \\
&= \frac{m}{b}\int_{-\frac{b}{2}}^{\frac{b}{2}} x^2 dx \\
&= \frac{m}{b}\left[ \frac{x^3}{3} \right]_{-\frac{b}{2}}^{\frac{b}{2}} \\
&= \frac{1}{12}mb^2
\end{align*}$$
同様にx軸まわりについても考えると
$$I_{x} = \frac{1}{12}ma^2$$
直交軸の定理より、この長方形板に垂直な軸(z軸)まわりの慣性モーメントは
$$I_{z} = I_{x} + I_{y} = \frac{1}{12}m(a^2 + b^2)$$
回転半径は
$$k_{x} = \sqrt{\frac{I_{x}}{m}} =\frac{\sqrt{a^2}}{2\sqrt{3}}~~k_{y} = \sqrt{\frac{I_{y}}{m}} =\frac{\sqrt{b^2}}{2\sqrt{3}}~~k_{z} = \sqrt{\frac{I_{z}}{m}} =\frac{\sqrt{a^2 + b^2}}{2\sqrt{3}}$$
よって、以下の表のようになります
| 慣性モーメント | 回転半径 |
| $$I_{x} = \frac{1}{12}ma^2$$ | $$k_{x} =\frac{\sqrt{a^2}}{2\sqrt{3}}$$ |
| $$I_{y} = \frac{1}{12}mb^2$$ | $$k_{y}=\frac{\sqrt{b^2}}{2\sqrt{3}}$$ |
| $$I_{z} = \frac{1}{12}m(a^2 + b^2)$$ | $$k_{z}=\frac{\sqrt{a^2 + b^2}}{2\sqrt{3}}$$ |