以下のような正六角形の断面二次モーメントを求めます
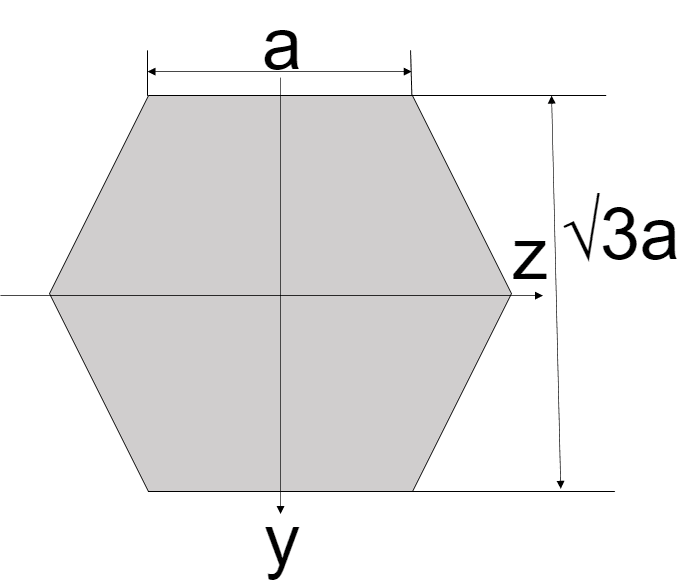
まずは、必要な長さを求めていきます
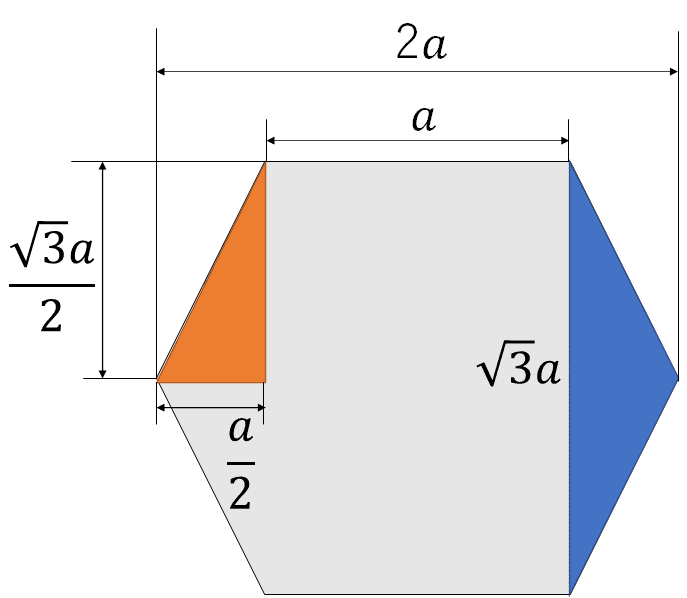
正六角形の一辺の長さをaとして、以下のような青い二等辺三角形と、オレンジの直角三角形を考えます

正六角形の内角は120°なので、青い三角形において、余弦定理よりxは
$$x^2 = a^2 + a^2 - 2\cdot a \cdot a \cos{120^\circ}$$
$$x = \sqrt{3}a$$
と求められます
zはxの半分の長さであり、オレンジの三角形において、三平方の定理より
$$y^2 + z^2 = a^2$$
$$y = \sqrt{a^2 - (\frac{\sqrt{3}a}{2})^2} = \frac{a}{2}$$
となります。また
$$l = 2y + a = 2a$$
となり、以下の図のようになります
これで必要な長さが得られたので、断面二次モーメントを求めていきます
まずは、z軸まわりの断面二次モーメントからです
以下のようにz軸からyだけ離れたところの微少距離dyを考える
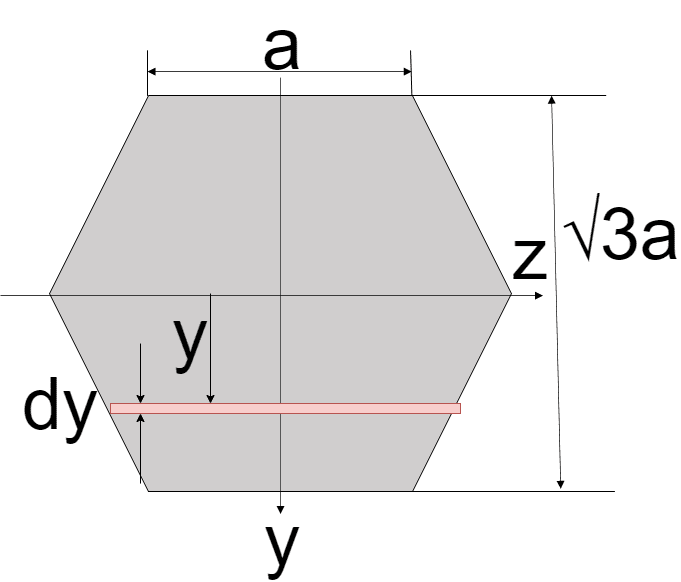
ここで、赤い微少部分の微少面積dAは近似的に長方形です
長方形の短辺はdyであり、長辺は高さによって異なります
長辺はz軸からの距離に対して反比例しますので
$$z = py + q~~~(p,qは定数)$$
とおいて考えます
長辺の長さは、z軸からの距離が0のときに2a、z軸からの距離が√3a/2のときにaであるため、代入すると
$$2a = q~,~a=\frac{\sqrt{3}}{2}p+q$$
より
$$p = -\frac{2}{\sqrt{3}}a~,~q = 2a$$
となるから、長辺の長さは
$$z = -\frac{2}{\sqrt{3}}y + 2a$$
となります
微少部分の面積dAは長辺×短辺で表されるので
$$dA = (-\frac{2}{\sqrt{3}}y + 2a)dy$$
となります
z軸まわりの断面二次モーメントは
$$\begin{align*}
I_{z}
&= \int_{A}^{} y^2 dA\\
&= 2\int_{0}^{\frac{\sqrt{3}}{2}a} (-\frac{2}{\sqrt{3}}y + 2a) y^2 dy\\
&= 2\left[ -\frac{y^4}{2\sqrt{3}} + \frac{2}{3}ay^3 \right]_{0}^{\frac{\sqrt{3}}{2}a}\\
&= 2(-\frac{9}{32\sqrt{3}}a^4 + \frac{\sqrt{3}}{4}a^4)\\
&= 2\cdot \frac{15\sqrt{3}}{96}a^4\\
&= \frac{5\sqrt{3}}{16}a^4
\end{align*}$$
と求められます
z軸から図の端までの長さは√3a/2であるから、断面係数は
$$Z_{z} = \frac{\frac{5\sqrt{3}}{16}a^4}{\frac{\sqrt{3}a}{2}} = \frac{5}{8}a^3$$
次にy軸まわりの断面二次モーメントについて考えます
以下のように青の長方形とオレンジの三角形に分けて考えます

右の三角形の重心を通るy'軸をとり、微少部分の面積を出して積分していく。というような、z軸まわりの断面二次モーメントと同様の求め方でも良いのですが、計算を簡単にするために、長方形と三角形の断面二次モーメントの公式を使用して解いていきます
右側の長方形において、yと平行で、長方形の重心を通る軸まわりの断面二次モーメントをIy1'とすると、公式より
$$I_{{y}_{1}}' = \frac{bh^3}{12} = \frac{\sqrt{3}}{96}a^4$$
長方形の面積をAとすると、y軸まわりの断面二次モーメントは、平行軸の定理より
$$\begin{align*}
I_{{y}_{1}}
&= I_{{y}_{1}}' + A\cdot (\frac{a}{4})^2\\
&= \frac{\sqrt{3}}{96}a^4 + \frac{\sqrt{3}}{32}a^4\\
&= \frac{\sqrt{3}}{24}a^4
\end{align*}$$
となります
また、右側の三角形において、yと平行で、三角形の重心を通る軸まわりの断面二次モーメントをIy2'とすると、公式より
$$I_{{y}_{1}}' = \frac{bh^3}{36} = \frac{\sqrt{3}}{288}a^4$$
三角形の面積をAとすると、y軸まわりの断面二次モーメントは、平行軸の定理より
$$\begin{align*}
I_{{y}_{2}}
&= I_{{y}_{2}}' + A\cdot (\frac{a}{2}+\frac{a}{6})^2\\
&= \frac{\sqrt{3}}{288}a^4 + \frac{\sqrt{3}}{9}a^4\\
&= \frac{11\sqrt{3}}{96}a^4
\end{align*}$$
となります
y軸まわりの断面二次モーメントは
$$I_{y} = 2 (I_{{y}_{1}}+I_{{y}_{2}}) = \frac{5\sqrt{3}}{16}a^4$$
となります
また、図心から端までの長さはaであるから、断面係数は
$$Z_{y} = \frac{\frac{5\sqrt{3}}{16}a^4}{a} =\frac{5\sqrt{3}}{16}a^3$$
となります