以下のような円錐の慣性モーメントを求めます
密度はρ、質量はmとします
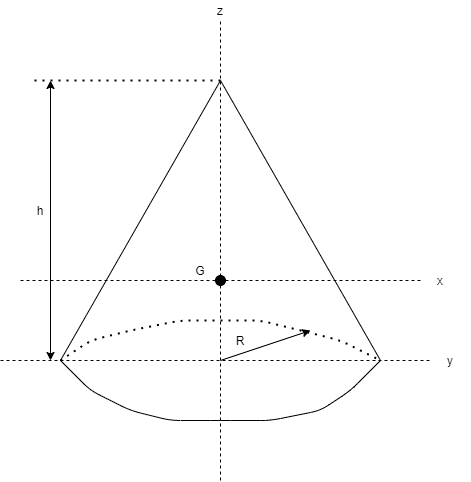
まずはz軸まわりの慣性モーメントを求めます
以下の図のように円錐をz軸に垂直な面でスライスします

スライスした円板部分の質量は$$dm = \rho \pi x^2 dz$$
円板のz軸まわりの慣性モーメントはこちらの記事より$$\frac{1}{2}mR^2$$であるから、スライスした部分の慣性モーメントは
$$dI = \frac{1}{2} \rho \pi x^2\cdot x^2 dz$$
高さと半径の比から$$R : x = h : h - z$$
$$x = \frac{R(h-z)}{h}$$となる
円錐の体積を考えると
$$m = \frac{1}{3}\rho \pi R^2 h$$
密度ρは$$\rho = \frac{3m}{\pi R^2 h}$$
0からhまでの範囲で積分すると
$$\begin{align*}
I_{z}
&= \int_{0}^{h} \frac{1}{2}\rho \pi x^4 dz\\
&= \frac{1}{2}\rho \pi \int_{0}^{h} x^4 dz\\
&= \frac{1}{2}\rho \pi \int_{0}^{h} (h-z)^4 dz\\
&= \frac{1}{2}\frac{\rho \pi R^4}{h^4}\left[ \frac{(h-z)^5}{5} \right]_{0}^{h}\\
&= \frac{\rho \pi R^4 h}{10}\\
&= \frac{3}{10}mR^2
\end{align*}
$$
次にy軸まわりの慣性モーメントについて考えます
z軸まわりと同様に円錐をスライスして考え、微少部分の質量を求めるところまでは同じです
こちらの記事より円板の慣性モーメントは$$\frac{1}{4}mR^2$$である
よってスライスした円板のy軸まわりの慣性モーメントは、平行軸の定理より
dI_{y}
&= \frac{1}{4}\rho \pi x^4 + dm z^2\\
&= \frac{1}{4}\rho \pi (\frac{R(h-z)}{h})^4 + \rho \pi (\frac{R(h-z)}{h})^2 z^2
\end{align*}$$
0~hの範囲で積分すると
I_{y}
&= \frac{1}{4}\rho \pi \frac{R^4}{h^4}\int_{0}^{h}(h-z)^4 dz + \frac{\rho \pi R^2}{h^2} \int_{0}^{h} z^2(h-z)^2 dz\\
&= \frac{\rho \pi R^4}{4h^4}\left[ \frac{(h-z)^5}{5} \right]_{0}^{h} + \frac{\rho \pi R^2}{h^2}\int_{0}^{h} z^4 -2hz^3 + h^2 z^2 dz\\
&= \frac{\rho \pi h R^4}{20} + \frac{\rho \pi R^2}{h^2}\left[ \frac{z^5}{5} - \frac{h}{2}z^4 + \frac{h^2 z^3}{3} \right]_{0}^{h}\\
&= \frac{\rho \pi h R^4}{20} + \frac{\rho \pi R^2}{h^2}(\frac{h^5}{5} - \frac{h^5}{2} + \frac{h^5}{3})\\
&= \frac{\rho \pi h R^4}{20} + \frac{\rho \pi h^3 R^2}{30}\\
&= \frac{3}{20}mR^2 + \frac{1}{10}mh^2
\end{align*}$$
x軸まわりの慣性モーメントは、平行軸の定理より
$$I_{x} = I_{y} - mz^2$$
円錐の重心位置は$$z = \frac{1}{4}h$$であるから
I_{x}
&= \frac{3}{20}mR^2 + \frac{1}{10}mh^2 - \frac{1}{16}mh^2\\
&= \frac{3}{20}mR^2 + \frac{3}{80}mh^2
\end{align*}$$
となる
回転半径は$$k = \sqrt{\frac{I}{m}}$$で求められるから
まとめて表にすると
円錐 | 慣性モーメント | 回転半径 |
| $$I_{x} = \frac{3}{20}mR^2 + \frac{3}{80}mh^2$$ | $$k_{x} = \frac{1}{4}\sqrt{\frac{3(4R^2 + h^2)}{5}}$$ | |
| $$I_{y}= \frac{3}{20}mR^2 + \frac{1}{10}mh^2$$ | $$k_{y} = \frac{1}{2}\sqrt{\frac{3R^2 + 2h^2}{5}}$$ | |
| $$I_{z} = \frac{3}{10}mR^2$$ | $$k_{z} = \sqrt{\frac{3}{10}}R$$ |