質量m、長さlの一様な細棒の慣性モーメントを導出する
下図のように、微少な長さをdx、dxまでの距離をxとして考えると
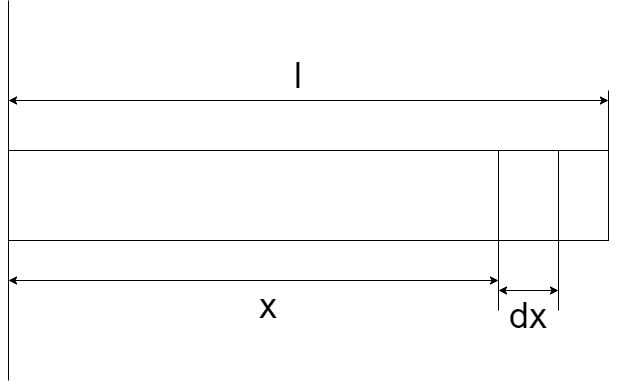
微少部分の質量が$$dm = \frac{m}{l}dx$$であるため
原点からx離れた微小部分dxの、原点まわりの慣性モーメントは
$$dI = x^2 dm =\frac{m}{l}x^{2}dx$$
となる
ここで下図の軸a、軸bそれぞれの軸まわりの慣性モーメントを考える
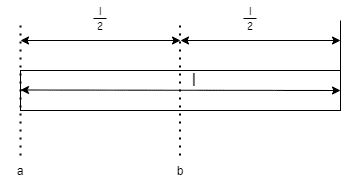
それぞれの積分範囲に注意して計算する
軸aが原点であれば、積分範囲は0~lとなるため
$$\begin{align*}
I_{a}
&= \int_0^l \frac{m}{l} x^2 dx\\
&= \frac{m}{l}\left[ \frac{x^3}{3} \right]_0^l\\
&= \frac{ml^2}{3}
\end{align*}$$
軸bが原点であれば、積分範囲は-l/2~l/2になるため
$$\begin{align*}
I_{b}
&= \int_{-\frac{l}{2}}^\frac{l}{2} \frac{m}{l} x^2 dx\\
&= \frac{m}{l}\left[ \frac{x^3}{3} \right]_{-\frac{l}{2}}^\frac{l}{2}\\
&= \frac{ml^2}{12}
\end{align*}$$
また、それぞれの回転半径は
$$k_{a} = \sqrt{\frac{I_{a}}{m}} = \frac{l}{\sqrt{3}} ~~~~~~~~~ k_{b} = \sqrt{\frac{I_{b}}{m}} = \frac{l}{2\sqrt{3}}$$
よって、以下の表のようになります
| 慣性モーメント | 回転半径 |
| $$I_{a} = \frac{ml^2}{3}$$ | $$k_{a} = \frac{l}{\sqrt{3}}$$ |
| $$I_{b} = \frac{ml^2}{12}$$ | $$k_{b} = \frac{l}{2\sqrt{3}}$$ |