以下のような円形の断面二次モーメントについて考えます
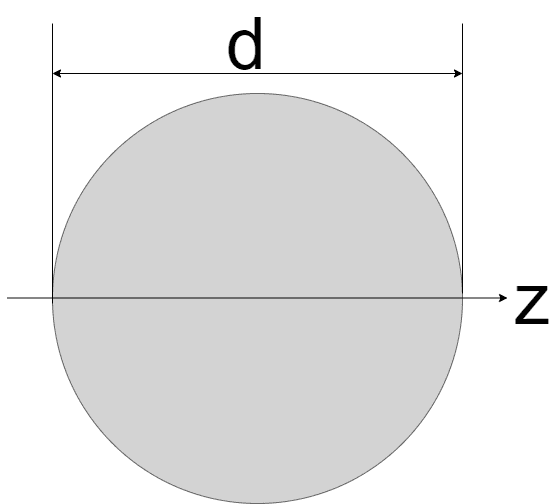
z軸からyだけ離れたところの微少距離dyを考える
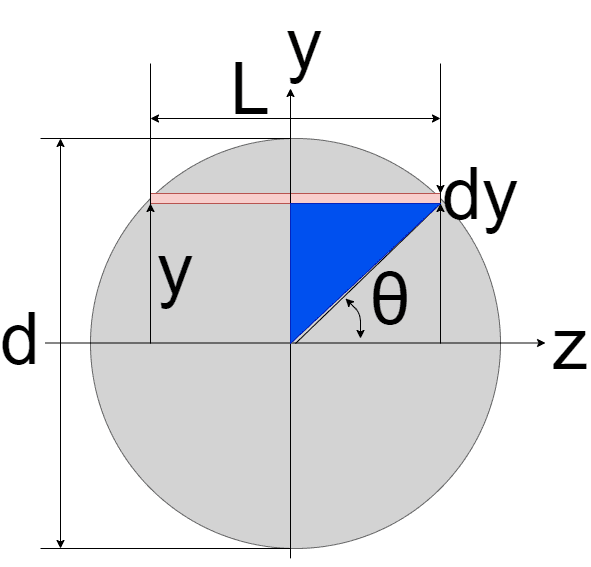
青い部分に注目すると、三平方の定理より
$$(\frac{L}{2})^2 + y^2 = (\frac{d}{2})^2$$
$$L = 2\sqrt{\frac{d^2}{4} - y^2}$$
であるから、赤色で示した微少部分の面積dAは
$$dA = 2\sqrt{\frac{d^2}{4} - y^2}dy$$
よって断面二次モーメントは
$$\begin{align*}
I_{z}
&= \int _A y^2 dA\\
&= \int_{-\frac{d}{2}}^{\frac{d}{2}}y^2 \cdot 2\sqrt{\frac{d^2}{4} - y^2} dy \cdots ①
\end{align*}$$
ここで\(y = \frac{d}{2}\sin \theta\)であるから、\( dy = \frac{d}{2}\cos{\theta}d\theta \)が成り立つ
また、積分範囲は
| $$y$$ | $$-\frac{d}{2}$$ | $$\rightarrow$$ | $$\frac{d}{2}$$ |
| $$\theta$$ | $$-\frac{\pi}{2}$$ | $$\rightarrow$$ | $$\frac{\pi}{2}$$ |
よって①を変換して計算すると
I_{z}
&= \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \frac{d^2}{4} \sin ^2 \theta \cdot 2 \cdot \sqrt{\frac{d^2}{4} - \frac{d^2}{4} \sin ^2 \theta} \cdot \frac{d}{2}\cos \theta \cdot d\theta\\
&= \frac{d^4}{8}\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \sin ^2 \theta cos ^2 \theta d\theta
\end{align*}$$
ここで、和と積の公式より
$$\sin \theta \cdot \cos \theta = \frac{1}{2}\sin{2\theta}$$
半角の公式より
$$\sin ^2 \theta = \frac{1 - \cos{4\theta}}{2}$$
であるから
$$\begin{align*}
I_{z}
&= \frac{d^4}{8}\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \sin ^2 \theta cos ^2 \theta d\theta\\
&= \frac{d^4}{32}\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \sin ^2 2\theta d\theta\\
& = \frac{d^4}{32}\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \frac{1 - \cos{4\theta}}{2} d\theta\\
& = \frac{d^4}{32}\left[ \frac{\theta}{2} - \frac{\sin{4\theta}}{8} \right]_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\\
& = \frac{\pi d^4}{64}
\end{align*}$$
と、求められる
断面の端までの長さをaとすると、断面係数はZ = I / aで求められるので
$$Z = \frac{\pi d^3}{32}$$
表で示すと
| 形状 | 断面二次モーメント | 断面係数 |
 | $$I_{z} = \frac{\pi d^4}{64}$$ | $$Z = \frac{\pi d^3}{32}$$ |