代表的な断面形状の断面二次モーメントと断面係数一覧と導出方法をまとめました
| 形状 | 断面二次モーメント | 断面係数 |
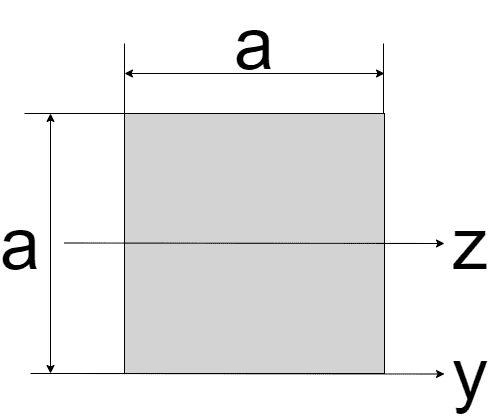
| 正方形
| $$I_{z} =\frac{a^4}{12}$$ $$I_{y} = \frac{a^4}{3}$$ | $$Z_{z} = \frac{a^3}{6}$$ $$Z_{y} = \frac{a^3}{3}$$ |
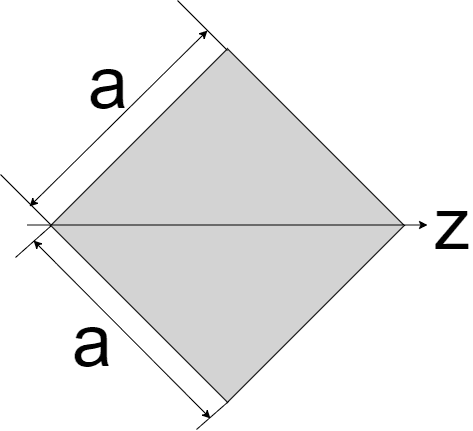
| 正方形(斜め)
| $$I_{z} = \frac{a^4}{12}$$ | $$Z_{z} = \frac{\sqrt{2} a^3}{12}$$ |
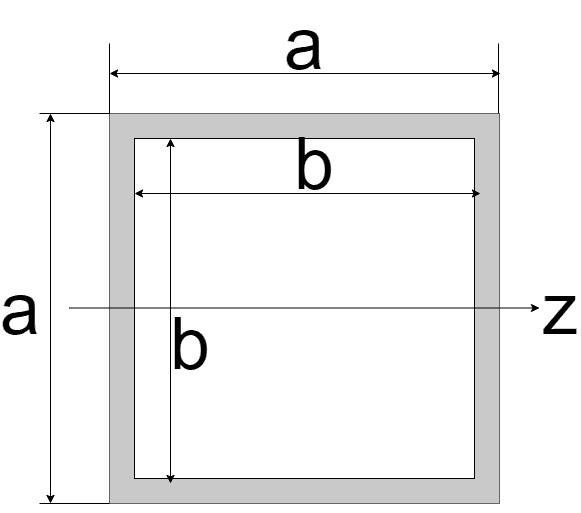
| 中空正方形
| $$I_{z} = \frac{a^4 - b^4}{12}$$ | $$Z_{z} = \frac{a^4 - b^4}{6a}$$ |
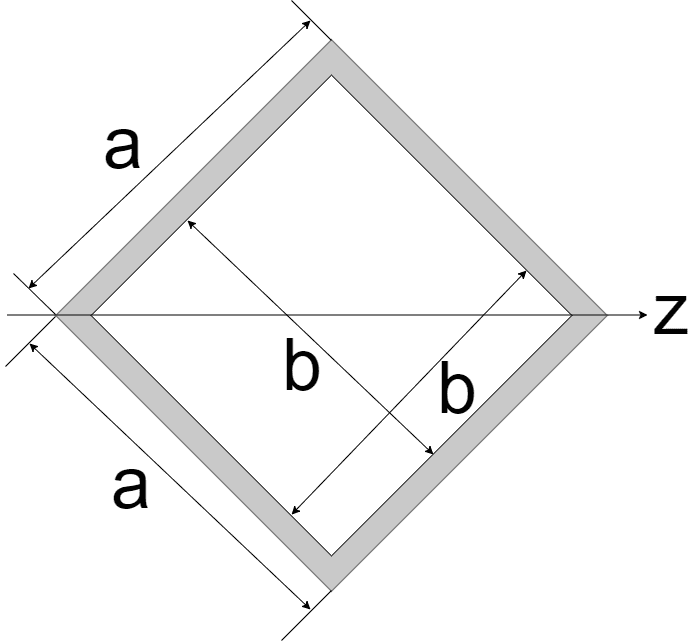
| 中空正方形(斜め)
| $$I_{z} = \frac{a^4 - b^4}{12}$$ | $$Z_{z} = \frac{a^4 - b^4}{6\sqrt{2}}$$ |
| 長方形
| $$I_{z} = \frac{bh^3}{12}$$ $$I_{y} = \frac{hb^3}{12}$$ $$I_{x} = \frac{bh^3}{3}$$ | $$Z_{z} = \frac{bh^2}{6}$$ $$Z_{y} = \frac{hb^2}{6}$$ $$Z_{x} = \frac{bh^2}{3}$$ |
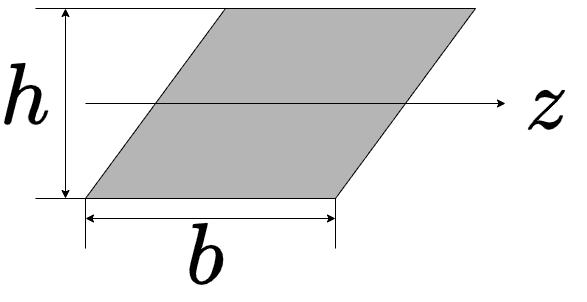
| 平行四辺形
| $$I_{z} = \frac{bh^3}{12}$$ | $$Z_{z} = \frac{bh^2}{6}$$ |
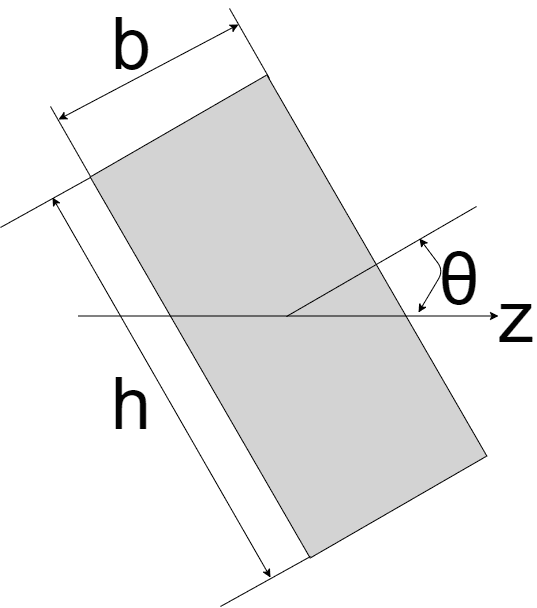
| 長方形(斜め)
| $$I_{z} = \frac{bh}{12}(h^{2} \cos ^{2}\theta + b^{2} \sin ^{2}\theta)$$ | $$Z_{z} = \frac{h^2 \cos ^2 \theta + b^2 \sin ^2 \theta}{6(h \cos{\theta} + b \sin{\theta})}$$ |
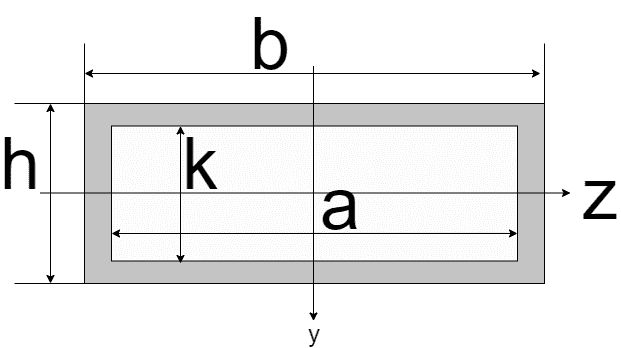
| 中空長方形
| $$I_{z} = \frac{bh^3 - ak^3}{12}$$ $$I_{y} = \frac{hb^3 - ka^3}{12}$$ | $$Z_{z} = \frac{bh^3 - ak^3}{6h}$$ $$Z_{y} = \frac{hb^3 - ka^3}{6b}$$ |
| 三角形
| $$I_{z} = \frac{bh^3}{36}$$ $$I_{y} = \frac{bh^3}{12}$$ | $$Z_{z} = \frac{bh^2}{24}$$ $$Z_{y} = \frac{bh^2}{12}$$ |
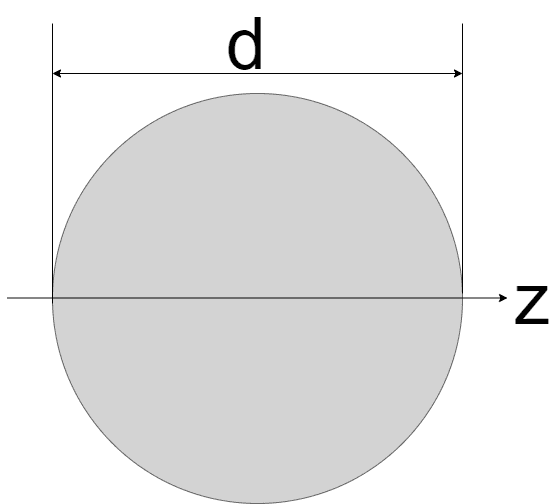
| 円形
| $$I_{z} = \frac{\pi d^4}{64}$$ | $$Z_{z} = \frac{\pi d^3}{32}$$ |
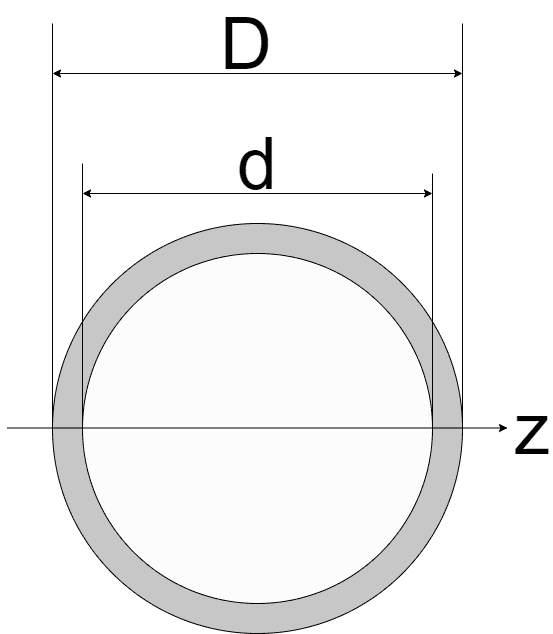
| 円筒
| $$I_{z} = \frac{\pi (D^4 - d^4)}{64}$$ | $$Z_{z} = \frac{\pi (D^4 - d^4)}{32D}$$ |
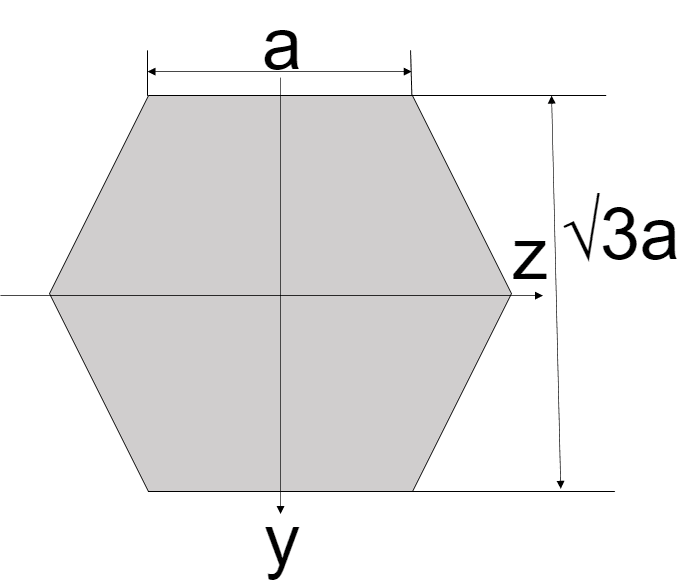
| 六角形
| $$I_{z} = \frac{5\sqrt{3}}{16}a^4$$ $$I_{y} = \frac{5\sqrt{3}}{16}a^4$$ | $$Z_{z} = \frac{5}{8}a^3$$ $$Z_{y} = \frac{5\sqrt{3}}{16}a^3$$ |
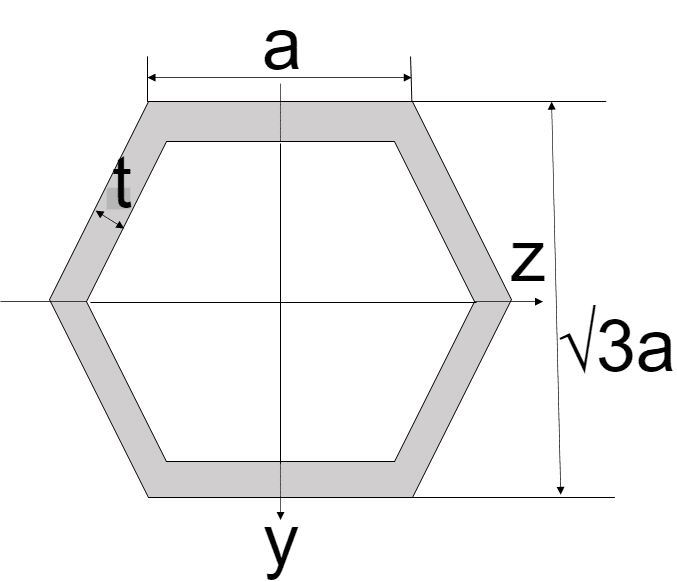
| 中空六角形
| $$I_{z} = \frac{5\sqrt{3}}{16}\{ a^4 - (a-\frac{2}{\sqrt{3}}t)^4 \}$$ $$I_{y} = \frac{5\sqrt{3}}{8}\{ a^4 - (a-\frac{2}{\sqrt{3}}t)^4 \}$$ | $$Z_{z} = \frac{5}{8a}\{ a^4 - (a-\frac{2}{\sqrt{3}}t)^4 \}$$ $$Z_{y} = \frac{5\sqrt{3}}{8a}\{ a^4 - (a-\frac{2}{\sqrt{3}}t)^4 \}$$ |
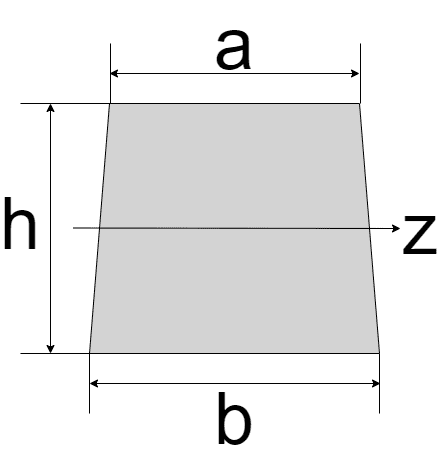
| 台形
| $$I_{z} = \frac{h^{3}(a^2 + 4ab + b^2)}{36(a+b)}$$ | $$Z_{z} = \frac{h^2 (a^2 + 4ab + b^2)}{12(a+2b)}$$ |
| 楕円
| $$I_{z} = \frac{\pi a^3 b}{4}$$ | $$Z_{z} = \frac{\pi a^2 b}{4}$$ |
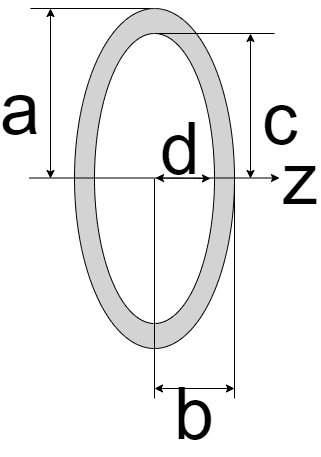
| 中空楕円
| $$I_{z} = \frac{\pi}{4}(a^3 b - c^3 d)$$ | $$Z_{z} = \frac{\pi (a^3 b - c^3 d)}{4a}$$ |
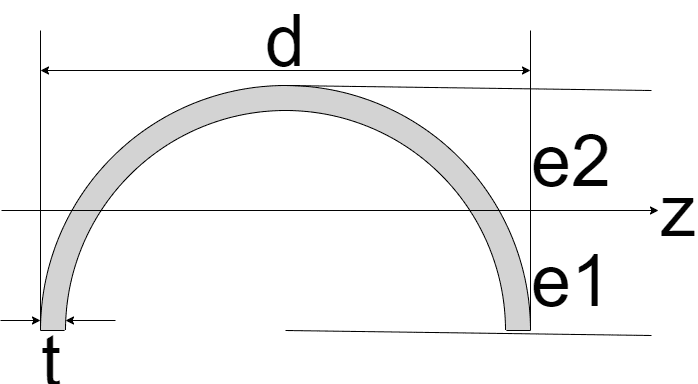
| 円弧
| $$I_{z} = \frac{\pi}{32}\{ d^4 - (d-2t)^4 \} - A{e_{1}}^2$$ $$A = \frac{\pi}{2}t(d - t)$$ $$e_{1} = \frac{3d^2 - 6td + 4t^2}{3\pi (d - t)}$$ $$e_{2} = \frac{d}{2} - e_{1}$$ | $$Z_{{z}_{1}} = \frac{I_{z}}{e_{1}}$$ $$Z_{{z}_{2}} = \frac{I_{z}}{e_{2}}$$ |
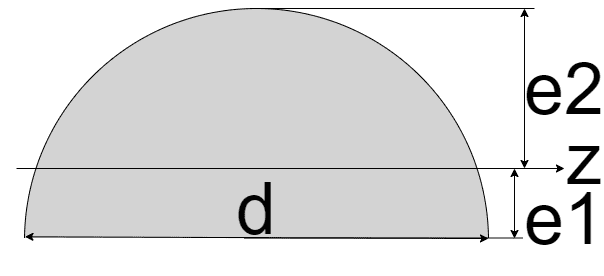
| 半円
| $$I_{z} = (\frac{\pi}{32} - \frac{1}{18\pi})d^4$$ $$e_{1} = \frac{2}{3\pi}d$$ $$e_{2} = (\frac{1}{2} - \frac{2}{3\pi})d$$ | $$Z_{{z}_{1}} = \frac{I_{z}}{e_{1}}$$ $$Z_{{z}_{2}} = \frac{I_{z}}{e_{2}}$$ |
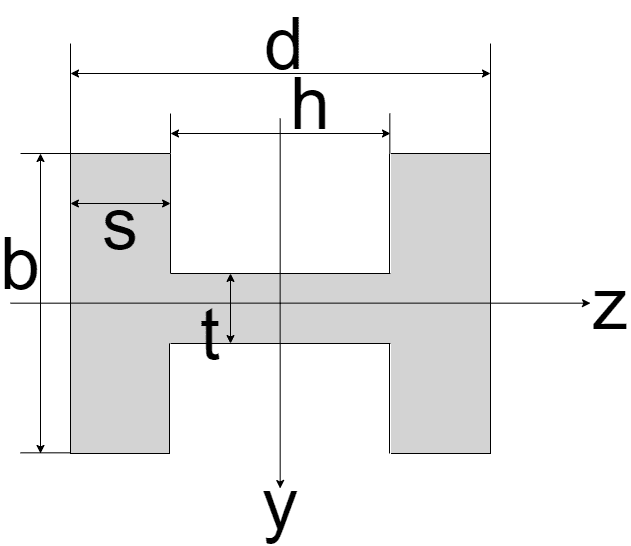
| H型
| $$I_{z} = \frac{2sb^3 + ht^3}{12}$$ $$I_{y} = \frac{bh^3 - h^3 (b-t)}{12}$$ | $$Z_{z} = \frac{2sb^3 + ht^3}{6b}$$ $$Z_{y} = \frac{bh^3 - h^3 (b-t)}{6d}$$ |
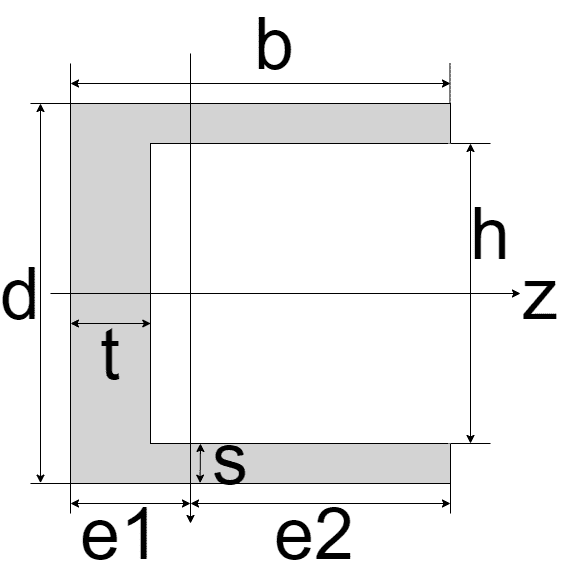
| コ型
| $$I_{z} = \frac{bd^3 - h^3 (b-t)}{12}$$ $$I_{y} = \frac{2sb^3 ht^3}{3} - A(b-e_{1})^2$$ $$A = bd - h(b-t)$$ $$e_{1} = b - \frac{2b^2 s + ht^2}{2bd - 2h(b-t)}$$ $$e_{2} = h - e_{1}$$ | $$Z_{z} = \frac{bd^3 - h^3 (b-t)}{6d}$$ $$Z_{{y}_{1}} = \frac{I_{y}}{e_{1}}$$ $$Z_{{y}_{2}} = \frac{I_{y}}{e_{2}}$$ |
| T型
| $$I_{z} = \frac{1}{3}\{ t{e_{1}}^3 + b{e_{2}^3 - (b-t)(e_{2}-s)^3} \}$$ $$e_{1} = d - \frac{d^2 t + s^2 (b -t)}{2\{ bs + t(d - s) \}}$$ $$e_{2} = \frac{d^2 t + s^2 (b -t)}{2\{ bs + t(d - s) \}}$$ | $$Z_{{z}_{1}} = \frac{I_{z}}{e_{1}}$$ $$Z_{{z}_{2}} = \frac{I_{z}}{e_{2}}$$ |
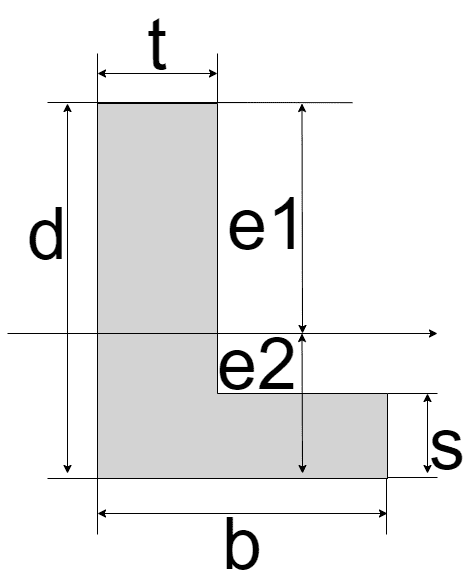
| L型
| $$I_{z} = \frac{1}{3}\{ t{e_{1}}^3 + b{e_{2}^3 - (b-t)(e_{2}-s)^3} \}$$ $$e_{1} = d - \frac{d^2 t + s^2 (b -t)}{2\{ bs + t(d - s) \}}$$ $$e_{2} = \frac{d^2 t + s^2 (b -t)}{2\{ bs + t(d - s) \}}$$ | $$Z_{{z}_{1}} = \frac{I_{z}}{e_{1}}$$ $$Z_{{z}_{2}} = \frac{I_{z}}{e_{2}}$$ |
導出方法
それぞれの導出方法を解説しています
計算ミス等ありましたらお知らせください