この導出方法では、長方形の断面二次モーメントを使います
長方形の断面二次モーメントの導出についてはこちらの記事をご覧ください
以下のようなI型(H型)の断面二次モーメントについて考えます
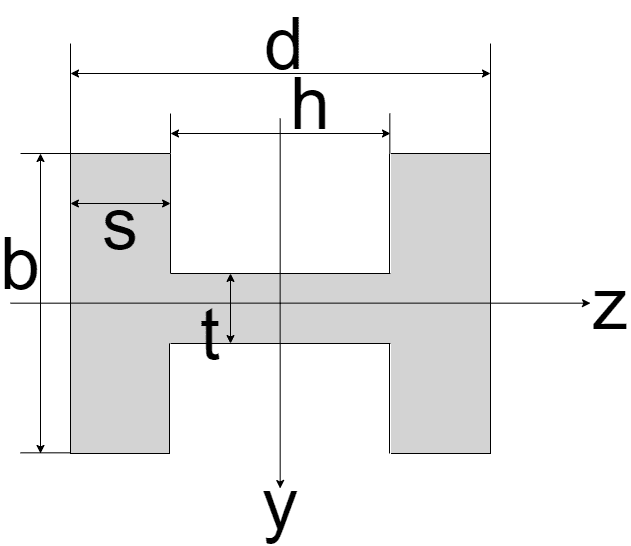
まずは、y軸まわりの慣性モーメントを求めます
面積bdの大きい長方形と、面積h(b -t)/2の小さい長方形に分けて考えます
長方形の断面二次モーメントの公式より、面積bdの大きい長方形の断面二次モーメントIbと面積h(b -t)/2の小さい長方形の断面二次モーメントIsは、それぞれ
$$I_{b} = \frac{bd^3}{12}$$
$$I_{s} = \frac{(b-t)h^3}{24}$$
小さい長方形は2つあるため、全体の断面二次モーメントは
$$I_{y} = I_{b} - 2I_{s} = \frac{bd^3 - h^3 (b - t)}{12}$$
となります
次に、z軸まわりの慣性モーメントを求めます
こちらも面積bdの大きい長方形と、面積h(b -t)/2の小さい長方形に分けて考えます
大きい長方形と小さい長方形の断面二次モーメントIbはさきほどと同様に
$$I_{b} = \frac{db^3}{12}$$
$$I_{s} = \frac{h(b-t)^3}{96}$$
平行軸の定理より、z軸まわりの小さい長方形の長方形の断面二次モーメントIzsは
I_{{z}_{s}}
&= I_{s} + A\{ \frac{(b+t)}{4} \}^2 \\
&= \frac{h(b-t)^3}{96} + \frac{h(b-t)}{2} \cdot \frac{(b+t)^2}{16}\\
&= \frac{h(b^3 - 3b^2 t + 3bt^2 - t^3)}{96} + \frac{h(b^3 + b^2 t - bt^2 - t^3)}{32}\\
&= \frac{h(4b^3 - 4t^3)}{96}\\
&= \frac{h(b^3 - t^3)}{24}
\end{align*}$$
小さい長方形は2つあるため、全体の断面二次モーメントは
$$\begin{align*}
I_{y}
&= I_{b} - 2I_{{z}_{s}}\\
&= \frac{db^3}{12} - \frac{h(b^3 - t^3)}{12}\\
&= \frac{2sb^3 + hb^3}{12} - \frac{h(b^3 - t^3)}{12}\\
&= \frac{2sb^3 + ht^3}{12}
\end{align*}$$
となります
断面の端までの長さをaとすると、断面係数はZ = I / aで求められるので
のように求められます
表で示すと
| 形状 | 断面二次モーメント | 断面係数 |
| I型(H型)
| $$I_{z} = \frac{2sb^3 + ht^3}{12}$$ | $$Z_{z} = \frac{2sb^3 + ht^3}{6b}$$ |
| $$I_{y} = \frac{bh^3 - h^3 (b-t)}{12}$$ | $$Z_{y} = \frac{bh^3 - h^3 (b-t)}{6d}$$ |