周波数解析法として、ボード線図やナイキスト線図、ベクトル軌跡があります
この記事では、ボード線図の書き方や意味について説明します
この記事で出てくる"ゲイン"や"周波数伝達関数"、"位相"について知らない場合は、まずこちらの記事からご覧ください
-
周波数伝達関数・周波数応答・周波数特性それぞれの意味を解説
続きを見る
ボード線図(ボーデ線図)
横軸に対数目盛で角周波数\(\omega\)をとり、縦軸にゲイン\(g\)をとったグラフをゲイン線図、位相\(\phi\)をとったグラフを位相線図と呼びます
そして、それらを角周波数を揃えて上下に並べたものをボード(ボーデ)線図と呼びます
縦軸は線形目盛(普通の目盛)ですが、横軸が対数目盛となっている片対数グラフで書きます
例えば、一次遅れ系\(G(s) = \frac{1}{s+1}\)のボード線図は以下のようになります
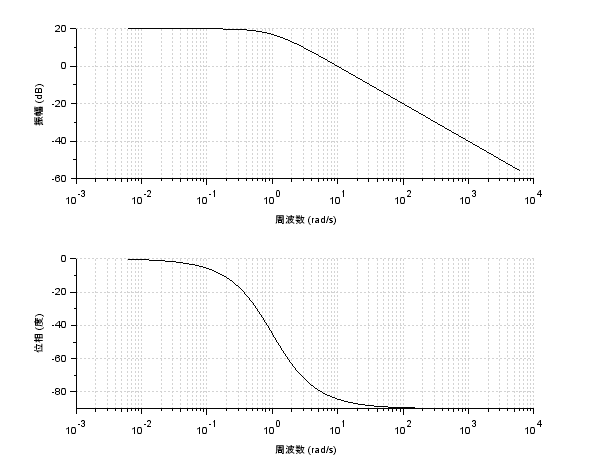
ボード線図は、システムの周波数特性を図で表現するための方法の一つです
様々な周波数に対する特性を視覚的に判断できることが、最大のメリットと言えるでしょう
基本要素の周波数特性
システムの特性は、様々な要素が存在しているため複雑になりますが、要素ごとに分割することができます
例えば、伝達関数\(G(s)\)が以下のような式で表されるときには
$$\begin{align*}
G(s) &= \frac{2(s+3)}{s(s+4)}\\
&= 2\cdot (s+3) \cdot \frac{1}{s}\cdot \frac{1}{s+4}
\end{align*}$$
のように分割できます
これらはそれぞれ
$$\begin{align*}
&比例要素:2\\
&一次進み要素:(s+3)\\
&積分要素:\frac{1}{s}\\
&一次遅れ要素:\frac{1}{s+4}\\
\end{align*}$$
のように、基本要素から構成されていることが分かります
基本要素が組み合わさった複雑なシステムの場合は、基本要素ごとにボード線図を書き、それらを組み合わせることでボード線図を書くことができます
ですので、複雑なシステムのボード線図を書くためには、まずは基本要素のボード線図の書き方を知ることが必要です
それでは、基本要素のボード線図の書き方について説明していきます
比例要素
比例要素の伝達関数は\(G(s) = K\)ですので、周波数伝達関数は\(G(j\omega) = K\)となります
ゲイン\(g\)は
$$\begin{align*}
g
&= 20\log _{10}|G(j\omega)|\\
&= 20\log_{10} K[dB]
\end{align*}$$
位相\(\phi\)は
$$\begin{align*}
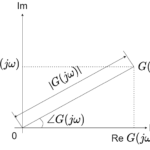
\phi
&= \tan ^{-1}\frac{Im~G(j\omega )}{Re~G(j\omega )}\\
&= \tan ^{-1}\frac{0}{0}\\
&= 0[deg]
\end{align*}$$
となります
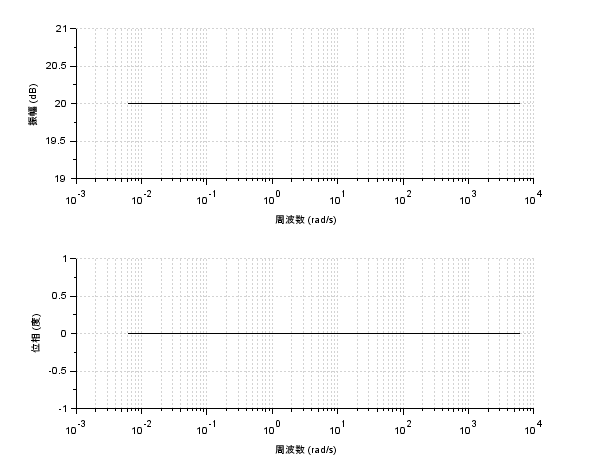
これらより、ゲインは一定で\(20\log_{10} K[dB]\)、位相は変わらないことが分かりますので、\(K=10\)としたボード線図は以下のようになります
微分要素
微分要素の伝達関数は\(G(s) = sT\)ですので、周波数伝達関数は\(G(j\omega) = j\omega T\)となります
ゲイン\(g\)は
$$\begin{align*}
g
&= 20\log _{10}|G(j\omega)|\\
&= 20\log_{10} \omega T[dB]
\end{align*}$$
位相\(\phi\)は
$$\begin{align*}
\phi
&= \tan ^{-1}\frac{Im~G(j\omega )}{Re~G(j\omega )}\\
&= \tan ^{-1}\frac{\omega T}{0}\\
&= \frac{\pi}{2}[deg]
\end{align*}$$
となります
これらより、ゲインは角周波数が\(\omega T >1\)のときは正の値、\(\omega T < 1\)のときは負の値になります
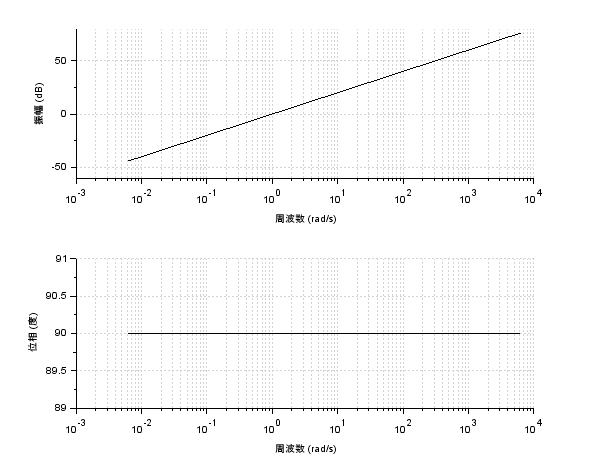
そして、位相は入力に対して常に90[deg]進むことが分かりますので、\(T=1\)としたボード線図は以下のようになります
積分要素
積分要素の伝達関数は\(G(s) = \frac{1}{sT}\)ですので、周波数伝達関数は\(G(j\omega) = \frac{1}{j\omega T}\)となります
ゲイン\(g\)は
$$\begin{align*}
g
&= 20\log _{10}|G(j\omega)|\\
&= 20\log_{10} \frac{1}{\omega T}\\
&= -20\log_{10}\omega T[dB]
\end{align*}$$
位相\(\phi\)は
$$\begin{align*}
\phi
&= \tan ^{-1}\frac{Im~G(j\omega )}{Re~G(j\omega )}\\
&= \tan ^{-1}\frac{0}{1} - \tan ^{-1}\frac{\omega T}{0}\\
&= -\frac{\pi}{2}[deg]
\end{align*}$$
となります
これらより、ゲインは角周波数が\(\omega T <1\)のときは正の値、\(\omega T > 1\)のときは負の値になります
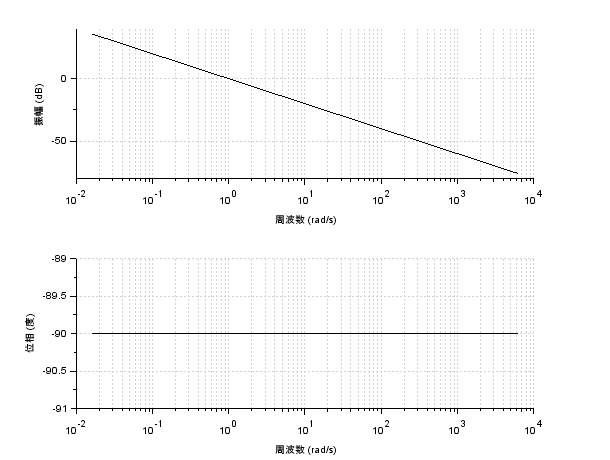
そして、位相は入力に対して常に90[deg]遅れることが分かりますので、\(T=1\)としたボード線図は以下のようになります
一次進み要素
一次進み要素の伝達関数は\(G(s) = 1+Ts\)ですので、周波数伝達関数は\(G(j\omega) = 1+j\omega T\)となります
ゲイン\(g\)は
$$\begin{align*}
g
&= 20\log _{10}|G(j\omega)|\\
&= 20\log_{10} \sqrt{(\omega T)^2 + 1}[dB]
\end{align*}$$
位相\(\phi\)は
$$\begin{align*}
\phi
&= \tan ^{-1}\frac{Im~G(j\omega )}{Re~G(j\omega )}\\
&= \tan ^{-1}\frac{\omega T}{1}\\
&= \tan ^{-1}\omega T[deg]
\end{align*}$$
となります
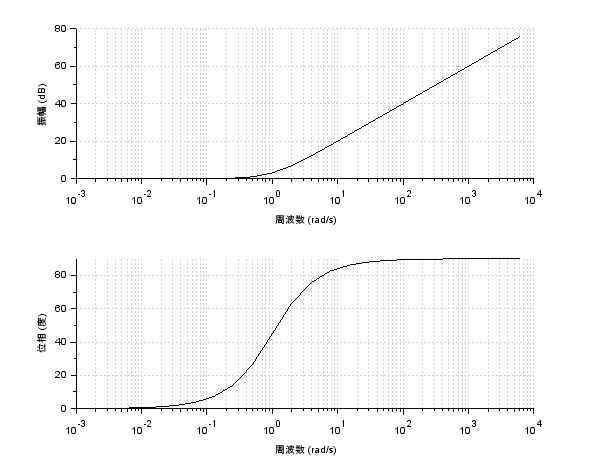
これらより、角周波数の大きさによってゲインと位相が決定することが分かります
・角周波数が十分に小さい場合:ゲインは\(g = 0[dB]\)、位相は\(\phi = 0[deg]\)
・角周波数が十分に大きい場合:ゲインは\(g = 20\log_{10} \omega[dB]\)、位相は\(\phi = 90[deg]\)
よって、\(T=1\)としたボード線図は以下のようになります
一次遅れ要素
一次遅れ要素の伝達関数は\(G(s) = \frac{K}{1+Ts}\)ですので、周波数伝達関数は\(G(j\omega) = \frac{K}{1+j\omega T}\)となります
ゲイン\(g\)は
$$\begin{align*}
g
&= 20\log _{10}|G(j\omega)|\\
&= 20\log_{10} \frac{K}{ \sqrt{(\omega T)^2 + 1}}[dB]
\end{align*}$$
位相\(\phi\)は
$$\begin{align*}
\phi
&= \tan ^{-1}\frac{Im~G(j\omega )}{Re~G(j\omega )}\\
&= \tan ^{-1}\frac{0}{K} - \frac{\omega T}{1}\\
&= -\tan ^{-1}\omega T[deg]
\end{align*}$$
となります
これらより、角周波数の大きさによってゲインと位相が決定することが分かります
・角周波数が十分に小さい場合:ゲインは\(g = 20\log_{10}K [dB]\)、位相は\(\phi = 0[deg]\)
・角周波数が十分に大きい場合:ゲインは\(g = -20\log_{10}\omega [dB]\)、位相は\(\phi = -90[deg]\)
よって、\(K=10~,~T=1\)としたボード線図は以下のようになります

折れ点周波数と折れ線近似
ここで、一次進み要素、一次遅れ要素のゲイン線図の曲がる点について考えます
上に挙げた例ですと、どちらも\(\omega = 10^{0}\)の位置で曲がり始めています
一次遅れ要素のゲイン\(g\)は、比例ゲイン\(K=10\)、時定数\(T=1\)であるから
$$g = 20\log_{10} \frac{10}{ \sqrt{(\omega)^2 + 1}}$$
となっています
\(\log_{10} 2 \approx 0.30102\)を使って近似すると、角周波数の変化により、以下のようにゲインは変化します
・\(\omega < 10^{0}\)のとき、ゲインは約\(20[dB]\)
・\(\omega = 10^{0}\)のとき、ゲインは\(20\log_{10} \frac{10}{ \sqrt{2}} \approx 20 - 3 = 17[dB]\)
・\(\omega = 10^{1}\)のとき、ゲインは\(20\log_{10} \frac{10}{ \sqrt{101}} \approx 20 - 20 = 0[dB]\)
そして、位相はゲイン線図の曲がりはじめたところ\(\omega = 10^{0}\)で、\(-45[deg]\)を通過しています
ゲイン線図が曲がりはじめるところ、位相が\(-45[deg]\)を通過するところの角周波数を折れ点周波数と呼びます
折れ点周波数は時定数の逆数\(\frac{1}{T}\)になります
上の例だと折れ点周波数は\(10^{0}\)と、時定数の逆数になっています
手書きで書く際には、折れ点周波数で一次遅れ要素の位相が\(-45[deg]\)、一次進み要素の位相が\(45[deg]\)になっていることは覚えておいてください
比例ゲインはそのままで、時定数を\(T=0.1,10\)としてそれぞれのボード線図を書くと
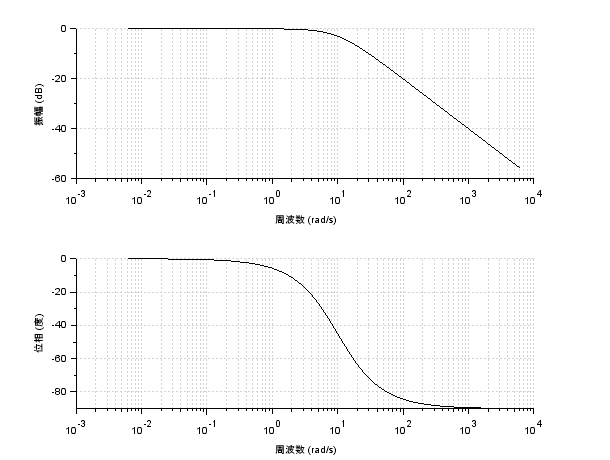
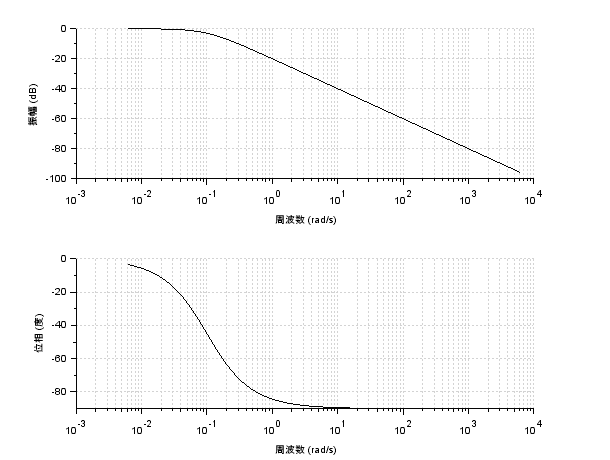
折れ点周波数はそれぞれ、\(10^{1},10^{-1}\)のようになっており、時定数の逆数であることが確認できました
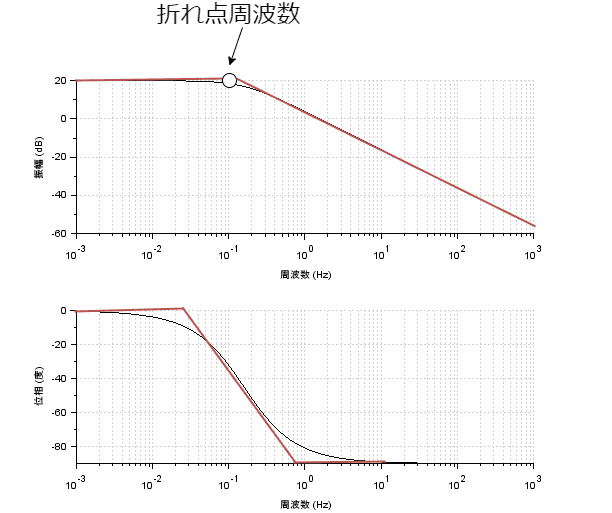
また、一次進み要素、一次遅れ要素のような、曲線のボード線図を直線近似したものを折れ線近似と呼びます
少し雑ですが、折れ線近似の図を載せておきます
二次遅れ要素
二次遅れ要素の伝達関数は\(G(s) = \frac{K\omega _{n}^2}{s^2 + 2\zeta \omega _{n}s + \omega _{n}^2}\)であるから、周波数伝達関数は\(G(j\omega) =\frac{K\omega _{n}^2}{-\omega ^2 + \omega _{n}^2 + j2\zeta \omega _{n}\omega}\)となります
ゲイン\(g\)は
$$\begin{align*}
g
&= 20\log _{10}|G(j\omega)|\\
&= 20\log_{10}\frac{K\omega _{n}^2}{\sqrt{(\omega _{n}^2 - \omega ^2)^2 + (2\zeta \omega _{n}\omega)^2}}[dB]
\end{align*}$$
位相\(\phi\)は
$$\begin{align*}
\phi
&= \tan ^{-1}\frac{Im~G(j\omega )}{Re~G(j\omega )}\\
&= \tan ^{-1}\frac{0}{K\omega _{n}^2} - \tan ^{-1}(\frac{2\zeta \omega _{n}\omega}{\omega _{n}^2 - \omega ^2})\\
&= -\tan ^{-1}(\frac{2\zeta \omega _{n}\omega}{\omega _{n}^2 - \omega ^2})[deg]
\end{align*}$$
となります
これらより、角周波数の大きさによってゲインと位相が決定することが分かります
・角周波数が十分に小さい場合:
$$g \approx 20\log_{10}\frac{K\omega _{n}^2}{\sqrt{\omega _{n}^4}} =20\log_{10}K[dB]$$
$$\phi \approx -\tan ^{-1}0 = 0[deg]$$
・角周波数が十分に大きい場合:
$$g \approx 20\log_{10}\frac{K\omega _{n}^2}{\omega ^2} \approx -40\log_{10}\omega [dB]$$
$$\phi \approx -\tan ^{-1}\frac{2}{\omega} \approx -180[deg]$$
・角周波数が固有角周波数\(\omega _{n}\)と同じ場合:
$$g = 20\log_{10}\frac{K\omega _{n}^2}{2\zeta \omega _{n}^2} = 20\log_{10}\frac{K}{2\zeta}$$
$$\phi = 90[deg]$$
\(\zeta = 0.01~,~K=1~,~\omega _{n} = 1\)としたときのボード線図は以下のようになります
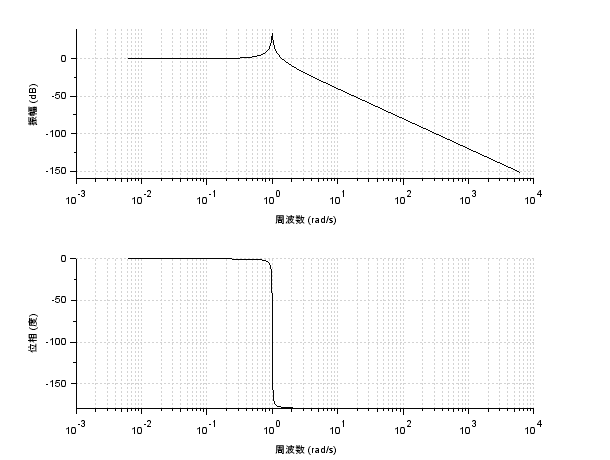
折れ点周波数は\(\omega _{n}\)、位相線図は折れ点周波数で\(-90[deg]\)となっているのが特徴です
式からもわかる通り、減衰係数\(\zeta\)の値が小さいほど、ゲイン線図の折れ点周波数でのピークは鋭くなります
むだ時間要素
入力信号を加えてから,出力信号が生じるまでの時間をむだ時間と呼びます
むだ時間を\(\tau\)とすると、むだ時間要素の伝達関数は\(G(s) = e^{-\tau s}\)ですので、周波数伝達関数は\(G(j\omega) = e^{-j\omega\tau}\)となります
オイラーの公式より\(e^{-j\omega\tau}= \cos {\omega \tau} - j\sin {\omega \tau}\)であるから
ゲイン\(g\)は
$$\begin{align*}
g
&= 20\log _{10}|G(j\omega)|\\
&= 20\log_{10} 1\\
&= 0[dB]
\end{align*}$$
位相\(\phi\)は
$$\begin{align*}
\phi
&= \tan ^{-1}\frac{Im~G(j\omega )}{Re~G(j\omega )}\\
&= \tan ^{-1}\frac{-\sin {\omega \tau}}{\cos {\omega \tau}}\\
&= -\tan ^{-1}\tan {\omega \tau}\\
&= -\omega \tau
\end{align*}$$
となります
これらより、ゲインは一定で\(0[dB]\)、位相は周波数が増加すると遅れることが分かりますので、\(\tau = 0.1\)としたボード線図は以下のようになります(近似を行っています)
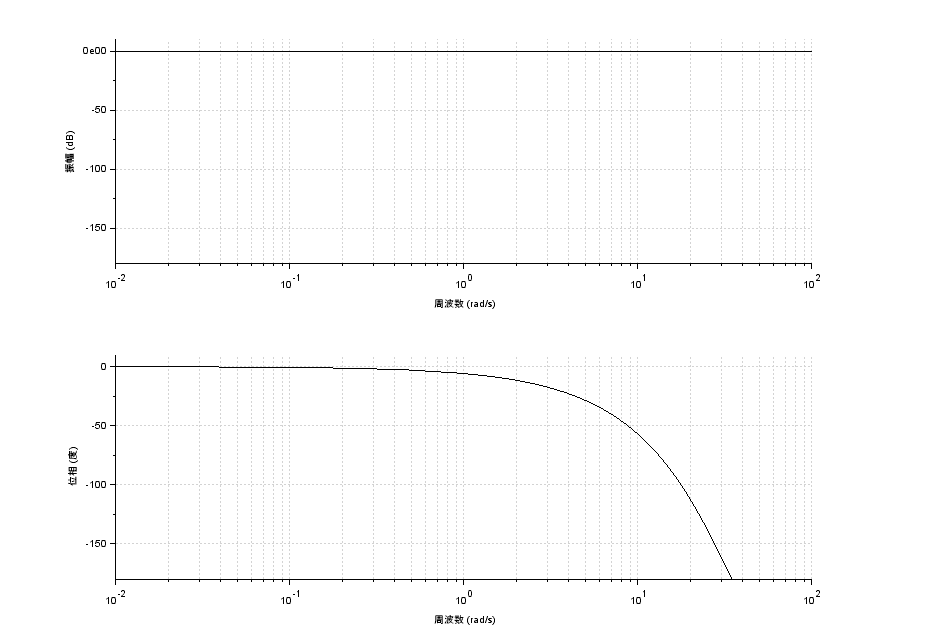
ボード線図の合成
ここまでで基本要素のボード線図の書き方をお伝えしてきました
ここまで理解できている方は、もうすでにボード線図を書けるようになるための道具は用意できました
あとは基本要素の組み合わせで、高次の伝達関数でもボード線図を書くことができます
次の伝達関数で試してみましょう
$$G(s) = \frac{s+10}{(s+1)(10s+1)}$$
まずは、要素ごとに分けていきます
$$\begin{align*}
G(s) &=\frac{s+10}{(s+1)(10s+1)}\\
&= 10\times (0.1s + 1)\times \frac{1}{s+1}\times \frac{1}{10s+1}\\
&= G_{1}(s) \times G_{2}(s) \times G_{3}(s) \times G_{4}(s)
\end{align*}$$
このように、比例要素\(G_{1}(s) = 10\)、一次進み要素\(G_{2}(s) = 0.1s + 1\)、一次遅れ要素\(G_{3}(s) = \frac{1}{s+1}~,~G_{4}(s) = \frac{1}{10s+1}\)に分解することができます
それぞれのボード線図を書くと、以下の図のようになります
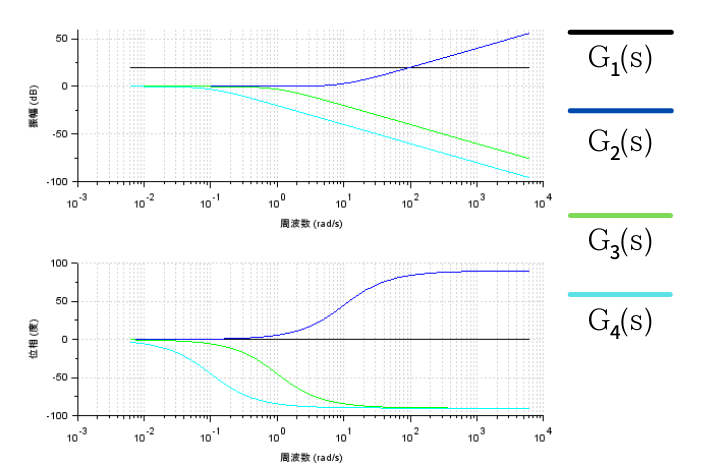
そして、重ね合わせた\(G(s)\)のボード線図を赤線で書くと
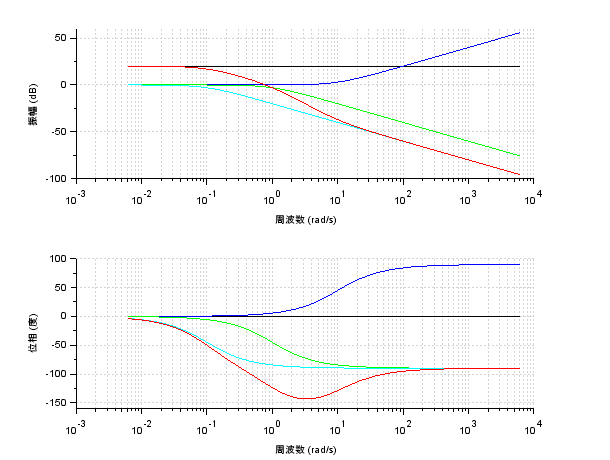
のようになりました
まずは、ゲイン線図から見ていくと
\(\omega < 10^{-1}\)では、比例要素のゲインが\(20[dB]\)であり、それ以外の要素は\(0[dB]\)であるため、それらを重ね合わせた\(G(s)\)のゲインは\(20[dB]\)付近になっています
\(\omega = 10^{-1}\)は、\(G_{4}(s)\)の折れ点周波数であり、\(-20[dB/dec]\)の傾きで減少しはじめ、それ以外の要素に変化は生じていないため、それらを重ね合わせた\(G(s)\)のゲインも\(-20[dB/dec]\)の傾きで減少しはじめます
\(\omega = 10^{0}\)は、\(G_{3}(s)\)の折れ点周波数であり、\(-20[dB/dec]\)の傾きで減少しはじめ、さらに\(G_{4}(s)\)の減少も継続しているので、それらを重ね合わせた\(G(s)\)のゲインは\(-40[dB/dec]\)の傾きで減少しはじめます
少しわかりにくいかもしれませんが、\(10-{-1} <\omega <10^{0}\)よりも\(10-{-0} <\omega <10^{1}\)の方が傾きが鋭くなっていることが図からも認識できます
\(\omega = 10^{1}\)は、\(G_{2}(s)\)の折れ点周波数であり、\(20[dB/dec]\)の傾きで増加しはじめ、\(G_{3}(s),G_{4}(s)\)の減少も継続しているので、それらを重ね合わせた\(G(s)\)のゲインは\(-20[dB/dec]\)の傾きで減少しはじめます
さらに角周波数が大きくなっていっても各要素に変化はないため、\(-20[dB/dec]\)の傾きで減少を続けます
次に位相線図を見てみると
\(\omega < 10^{-1}\)では、全ての要素で位相の進みや遅れは見られないので、それらを重ね合わせた\(G(s)\)の位相でもずれは見られません
\(\omega = 10^{-1}\)は、\(G_{4}(s)\)の折れ点周波数であり、\(-45[deg]\)となっています。それ以外の要素ではほとんどずれは見られないので、\(G(s)\)の位相もおよそ\(-45[deg]\)となります
\(\omega = 10^{0}\)は、\(G_{3}(s)\)の折れ点周波数であり、\(-45[deg]\)となっています。\(G_{4}(s)\)は\(-90[deg]\)で、それ以外の要素ではほとんどずれは見られないので、\(G(s)\)の位相はおよそ\(-135[deg]\)となります
\(\omega = 10^{1}\)は、\(G_{2}(s)\)の折れ点周波数であり、\(45[deg]\)となっています。\(G_{3}(s),G_{4}(s)\)は\(-90[deg]\)で、\(G_{1}(s)\)ではずれがないため、\(G(s)\)の位相はおよそ\(-135[deg]\)となります
\(\omega > 10^{2}\)では、\(G_{3}(s),G_{4}(s)\)は\(-90[deg]\)で、\(G_{2}(s)\)は\(90[deg]\)で、\(G_{1}(s)\)ではずれがないため、\(G(s)\)の位相はおよそ\(-90[deg]\)となります
なぜ足し合わせるだけで良いのか
各要素のボード線図を足し合わせるだけで、高次の伝達関数のボード線図が簡単に書けることが分かりました
ですが、なぜ足し合わせるだけで良いのでしょうか
その理由を説明します
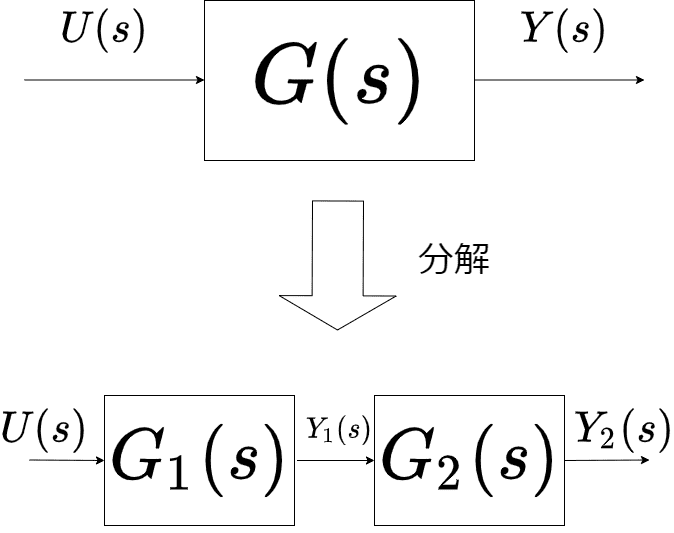
あるシステムに正弦波の入力信号\(U(s)\)を加え、出力信号\(Y(s)\)が得られたとします
この伝達関数\(G(s)\)を\(G_{1}(s),G_{2}(s)\)に分解して、\(U(s)\)の振幅を\(A\)、\(Y_{1}(s)\)の振幅を\(B\)、\(Y_{2}(s) = Y(s)\)の振幅を\(C\)、とすると、入力と出力の振幅比は
$$\frac{C}{A} = \frac{C}{B} \times \frac{B}{A}\cdots ①$$
となります
ゲイン\(g\)は\(20\log_{10}|G(j\omega)|\)であるため、①の式の両辺の対数をとると
$$\begin{align*}
20\log_{10}\frac{C}{A} &= 20\log_{10}\frac{C}{B} \times \frac{B}{A}\\
20\log_{10}\frac{C}{A} &= 20\log_{10}\frac{C}{B} + 20\log_{10}\frac{B}{A}\\
g = g_{1} + g_{2}
\end{align*}$$
のようになります
分解した伝達関数\(G_{1}(s)~,~G_{2}(s)\)のゲイン\(g_{1}~,~g_{2}\)の足し合わせで元の伝達関数\(G(s)\)のゲイン\(g\)が表されることが分かりました
位相線図も同様にできます
まとめ
この記事では、ボード線図の書き方について1から説明していきました
複雑な伝達関数であっても、基礎要素に分解して足し合わせるだけで簡単に書けることが理解していただけたら嬉しいです
説明下手な文章を最後までお読みいただきありがとうございました
Scilab
今回のボード線図は「Scilab」というMATLABに似たソフトを使って作成しました
Scilabは無料ソフトで、MATLABよりも軽いので非常に使いやすいです
実際に書いて試してみたい方は、ぜひ使ってみてください
プログラムの書き方については以下の記事が参考になると思います
-
Scilabでボード線図を描いてみる
続きを見る
また、むだ時間をボード線図で書くときには近似を使わなければならないため、少し工夫が必要です
-
Scilabでむだ時間要素のボード線図を描く方法
続きを見る
追記:ボード線図・ベクトル軌跡描画ツール
閲覧者様から、簡単にボード線図とベクトル軌跡が書けるツールを教えていただきました
むだ時間要素や高次の伝達関数は書けませんが、基本要素だけを確認したいなら、Scilabよりもこちらの方が楽かもしれません