伝達関数\(G(s)\)の分母多項式が\(s\)の二次式以下の場合には、\(分母多項式=0\)とした特性方程式から極を求めることで、制御系が安定かどうかを調べることができます
-
制御系システムの安定性と極
続きを見る
しかし、分母多項式が三次式以上である場合には、上記の方法よりも簡単なものがあります
それが「ラウスの安定判別法」です
この記事では、ラウスの安定判別法について説明していきます
ラウスの安定判別法
ラウスの安定判別法は、伝達関数\(G(s)\)の分母多項式の係数を使って制御系が安定かどうかを調べます
不安定な場合は、不安定な極の個数を求めることもできます
伝達関数\(G(s)\)の分母多項式が、次のような方程式であるとします
$$a_{0}s^n + a_{1}s^{n-1} + a_{2}s^{s-2} + \cdots + a_{n-1}s + a_{n} = 0$$
ラウス配列の作成
分母多項式の係数に注目して、以下のような配列に並べます
| $$s^n$$ | $$a_{0}$$ | $$a_{2}$$ | $$a_{4}$$ | $$a_{6}$$ | ・・・ |
| $$s^{n-1}$$ | $$a_{1}$$ | $$a_{3}$$ | $$a_{5}$$ | ・・・ | ・・・ |
| $$s^{n-2}$$ | $$b_{1} = \frac{a_{1}a_{2}-a_{0}a_{3}}{a_{1}}$$ | $$b_{2} = \frac{a_{1}a_{4}-a_{0}a_{5}}{a_{1}}$$ | $$b_{3} = \frac{a_{1}a_{6}-a_{0}a_{7}}{a_{1}}$$ | ・・・ | ・・・ |
| $$s^{n-3}$$ | $$c_{1} = \frac{b_{1}a_{3}-a_{1}b_{2}}{b_{1}}$$ | $$c_{2} = \frac{b_{1}a_{5}-a_{1}b_{3}}{b_{1}}$$ | $$c_{3} = \frac{b_{1}a_{7}-a_{1}b_{4}}{b_{1}}$$ | ・・・ | ・・・ |
| $$s^{n-4}$$ | $$d_{1} = \frac{c_{1}b_{2}-b_{1}c_{2}}{c_{1}}$$ | $$d_{2} = \frac{c_{1}b_{3}-b_{1}c_{3}}{c_{1}}$$ | ・・・ | ・・・ | ・・・ |
| ︙ | ︙ | ︙ | ︙ | ︙ | ︙ |
| $$s^0$$ | $$$$ | $$0$$ |
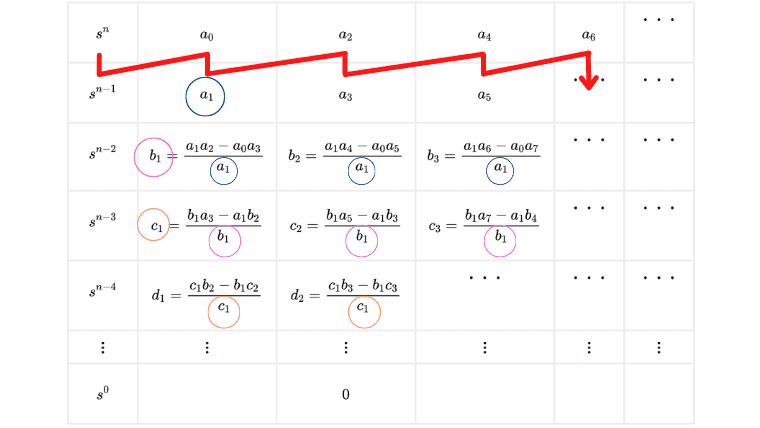
このような配列をラウス配列と呼びます
最高次\(n\)の係数から順番に、赤の矢印のようにジグザグに並べていきます
また、丸で囲んだように、3行目以降の分数の分母はその上の行の1列目の数になります
3行目以降の分数の分子は、たすき掛けのような形で表されています
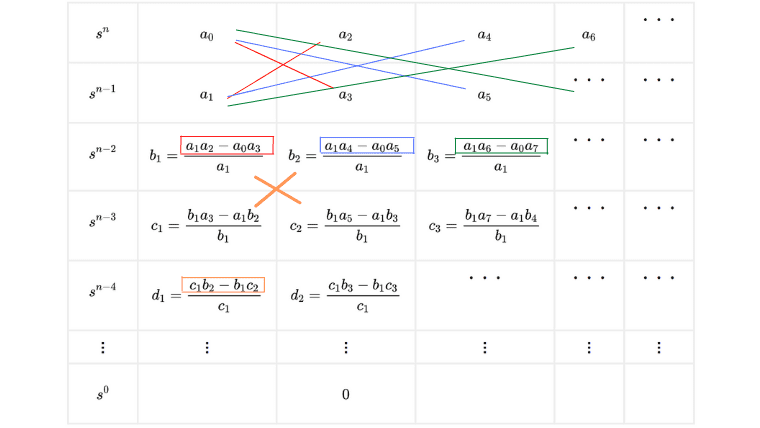
この計算を繰り返していき、\(s^0\)のところまで順番に埋めていきます
安定判別
ラウス配列が完成したら、1列目の値を上から順番に見ていきます(上の図であれば\(b_{1}~,~c_{1}~,~d_{1}\cdots\))
安定判別は以下のように行います
・1列目の値がすべて正の数・・・制御系は安定
・1列目に負の数が存在する・・・制御系は不安定であり、不安定な極の個数は、正負の符号が変わる回数分存在する
注意点
ラウス配列の作成を行う前に以下の二点を確認しておきましょう
・係数はすべて正の値である
・多項式の各次数に項が存在する
この2点を満たしていない場合は、ラウス配列を作成せずに、制御系は安定していないと判断できます
練習問題
ラウスの安定判別法の演習をしてみましょう
以下の伝達関数\(G_{1}(s)~,~G_{2}(s)\)を持つ制御系が安定かどうか判断してください
不安定である場合は、不安定な極の個数を求めてください
(1)
$$G_{1}(s) = \frac{1}{s^2 + 2s - 8}$$
(2)
$$G_{2}(s) = \frac{1}{2s^3 + 4s^2 + 3s + 9}$$
【解答】
(1)
分母多項式の係数を確認してみると\(1~,~2~,~-8\)となっており、係数に負の数が含まれるため不安定だと判断できます
極の値は
$$+4,-2$$
となります
(2)
係数を確認してみると\(2~,~4~,~3~,~9\)となっています
分母多項式の係数はすべて正であり、多項式の各次数に項が存在するので、ラウスの安定判別法を使います
ラウス配列を作成すると
| $$s^3$$ | $$2$$ | $$3$$ |
| $$s^2$$ | $$4$$ | $$9$$ |
| $$s^1$$ | $$\frac{12-18}{4} = -\frac{3}{2}$$ | $$0$$ |
| $$s^0$$ | $$\frac{-\frac{3}{2}\times 9}{-\frac{3}{2}} = 9$$ | $$0$$ |
のようになります
1列目の値を確認してみると\(2\rightarrow 4\rightarrow -\frac{3}{2}\rightarrow 9\)となっています
\(4\rightarrow -\frac{3}{2}\)と\(-\frac{3}{2}\rightarrow 9\)の2回符号が変わっています
よって、この制御系は不安定であり、不安定な極は2つになります
計算の途中で値が0の要素が出てくる場合
ラウス配列を作成するとき、0の要素が出てくる場合があります
要素に0が出てくるときには、以下のように計算を行います
ある行の第一列目に0の要素が出てくる場合
以下の伝達関数\(G_{3}(s)\)を持つ制御系が安定かどうか判断してください
$$G_{3}(s) = \frac{1}{s^5 + 2s^4 + 3s^3 + 6s^2 + s + 3}$$
同じように、ラウス配列を作成していくと
| $$s^5$$ | $$1$$ | $$3$$ | $$1$$ |
| $$s^4$$ | $$2$$ | $$6$$ | $$3$$ |
| $$s^3$$ | $$\color{red}{\frac{2\cdot 3 - 6\cdot 1}{2}=0}$$ | $$\frac{2\cdot 1 - 2\cdot 3}{2}=-\frac{1}{2}$$ | $$0$$ |
| $$s^2$$ | |||
| $$s^1$$ | |||
| $$s^0$$ |
のように、第一列の値が0になってしまいました
次の行の計算のときに分母の値が0になってしまうため、このままでは計算を進めていくことができません
このような場合は、0を小さな正の値\(0<\varepsilon \ll 1\)と置き換えて計算をすすめます
| $$s^5$$ | $$1$$ | $$3$$ | $$1$$ |
| $$s^4$$ | $$2$$ | $$6$$ | $$3$$ |
| $$s^3$$ | $$\varepsilon$$ | $$\frac{2\cdot 1 - 2\cdot 3}{2}=-\frac{1}{2}$$ | $$0$$ |
| $$s^2$$ | $$c_{1}$$ | $$3$$ | |
| $$s^1$$ | $$d_{1}$$ | $$0$$ | |
| $$s^0$$ | $$3$$ | $$0$$ |
\(c_{1},d_{1}\)を求めていきます
$$c_{1} = \frac{6\varepsilon+1}{\varepsilon} = 6 + \frac{1}{\varepsilon}$$
\(\varepsilon\)は小さい正の値であるから、\(\frac{1}{\varepsilon} \gg 6\)となるため
$$c_{1} \approx \frac{1}{\varepsilon}$$
$$d_{1} = \frac{-\frac{1}{2}c_{1} - 3\varepsilon}{c_{1}} = -\frac{1}{2}-\frac{3\varepsilon}{c_{1}}$$
\(\varepsilon\)は小さい正の値であるから、\(\frac{3\varepsilon}{c_{1}} \ll \frac{1}{2}\)となるため
$$d_{1} \approx -\frac{1}{2}$$
のようになります
よって、ラウス配列は
| $$s^5$$ | $$1$$ | $$3$$ | $$1$$ |
| $$s^4$$ | $$2$$ | $$6$$ | $$3$$ |
| $$s^3$$ | $$\varepsilon$$ | $$\frac{2\cdot 1 - 2\cdot 3}{2}=-\frac{1}{2}$$ | $$0$$ |
| $$s^2$$ | $$\frac{1}{\varepsilon}$$ | $$3$$ | |
| $$s^1$$ | $$-\frac{1}{2}$$ | $$0$$ | |
| $$s^0$$ | $$3$$ | $$0$$ |
のようになります
1列目の値を確認してみると2度符号が変わっていることが分かります
ですので、この制御系は不安定であり、不安定な極は2つあることになります
ある行の要素が全て0である場合
以下の伝達関数\(G_{4}(s)\)を持つ制御系が安定かどうか判断してください
$$G_{4}(s) = \frac{1}{s^4 + 2s^3 + 4s^2 + 2s^1 + 3}$$
同じように、ラウス配列を作成していくと
| $$s^4$$ | $$1$$ | $$4$$ | $$3$$ |
| $$s^3$$ | $$2$$ | $$2$$ | $$0$$ |
| $$s^2$$ | $$\frac{2\cdot 4 - 1\cdot 2}{2} = 3$$ | $$\frac{2\cdot 3 - 0}{2} = 3$$ | |
| $$s^1$$ | $$\color{red}{0}$$ | $$\color{red}{0}$$ | |
| $$s^0$$ |
のように、4行目の要素が全て0になってしまいました
このような場合は、1つ上の行に注目して、以下のような方程式\(A(x)\)を作成します
$$A(x) = 3s^2 + 3$$
\(A(x) = 0\)とした式を、補助方程式と呼びます
補助方程式を整理して
$$s^2 + 1 = 0$$
この方程式で伝達関数\(G_{4}(s)\)の分母多項式を割ると、商は\(s^2 + 2s + 3\)となりますから
$$s^4 + 2s^3 + 4s^2 + 2s^1 + 3=(s^2 + 1)(s^2 + 2s + 3) = 0$$
より、極の値は\(\pm j~,~-1\pm j\sqrt{2}\)となるのが分かります
極の実部は全て負になっていますので、この制御系は安定だと判断できます
まとめ
伝達関数の分母多項式が高次であれば、ラウスの安定判別法がとても便利です
ラウス配列を作成し、1列目の符号の入れ替わりの数から制御系が安定かどうか判断できます
ラウスの安定判別法を使う前に以下の2点に注意
・係数はすべて正の値である
・多項式の各次数に項が存在する
【参考】
https://ja.wikipedia.org/wiki/%E3%83%A9%E3%82%A6%E3%82%B9%E3%83%BB%E3%83%95%E3%83%AB%E3%83%93%E3%83%83%E3%83%84%E3%81%AE%E5%AE%89%E5%AE%9A%E5%88%A4%E5%88%A5%E6%B3%95