今回の導出方法では、三角形と長方形の断面二次モーメントの公式と、三角形の重心位置を使用します
これらについては、断面二次モーメントの公式一覧をご覧ください
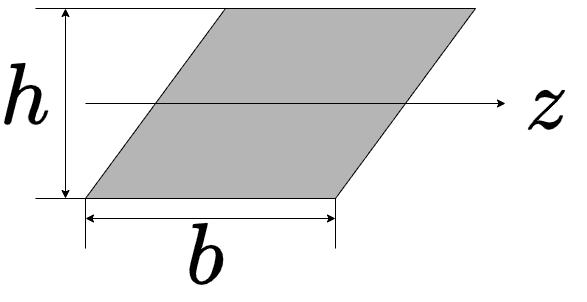
以下のような平行四辺形の断面二次モーメントを求めます
まずは、2つの赤い三角形と青い長方形に分けて考えます
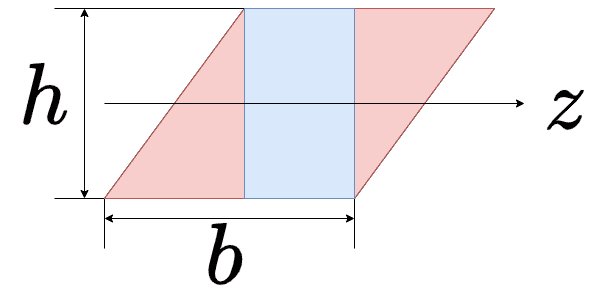
2つの方法がありますので、分けて説明します
方法1:三角形を平行移動
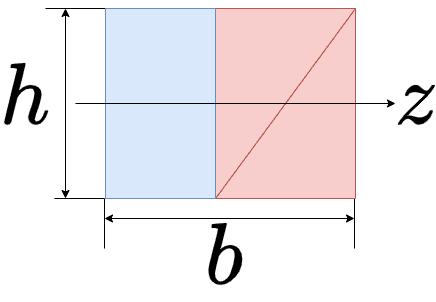
左の三角形を平行移動させると、幅b、高さhの長方形になります
断面二次モーメントは長方形と同じになるので、z軸まわりの断面二次モーメントは
$$I_{z} = \frac{bh^3}{12}$$
断面係数は
$$Z_{z} = \frac{\frac{bh^3}{12}}{\frac{h}{2}} = \frac{bh^2}{6}$$
方法2:断面二次モーメントを足し合わせる

上図のように\(b_{1}~,~b_{2}\)を設定します
青い長方形のz軸まわりの断面二次モーメントは
$$I_{z2} = \frac{b_{2}^3 h}{12}$$
赤い三角形の重心を通る軸まわりの断面二次モーメントは
$$I_{z1'} = \frac{b_{1}^3 h}{36}$$
平行軸の定理より、三角形のz軸まわりの断面二次モーメントは
$$\begin{align*}
I_{z1}
&= I_{z1'} + Ad^2\\
&= \frac{b_{1}^3 h}{36} +\frac{b_{1}h}{2}\times (\frac{h}{2}-\frac{h}{3})^2\\
&= \frac{b_{1}^3 h}{36} + \frac{b_{1}^3 h}{72}\\
&= \frac{b_{1}^3 h}{24}
\end{align*}$$
となるので、これらを足し合わせると、平行四辺形のz軸まわりの断面二次モーメントが求まる
$$\begin{align*}
I_{z}
&= 2I_{z1} + I_{z2}\\
&= \frac{b_{1}h^3 + b_{2}h^3}{12}\\
&= \frac{bh^3}{12}
\end{align*}$$
断面係数は
$$Z_{z} = \frac{\frac{bh^3}{12}}{\frac{h}{2}} = \frac{bh^2}{6}$$