【高校数学】三角比・三角関数の全ての公式の証明方法を解説します

高校数学で学ぶ三角比・三角関数は、苦手意識がある人も多いはず

三角比・三角関数は覚えるべき公式が多く、紛らわしいものもたくさんあるため、いざとなったときには自らで導出できるようにしておくと便利です

この記事では、三角比・三角関数の公式一覧と、その証明方法について解説します

公式一覧

まずは公式一覧を載せておきます

基本公式

$$\tan{\theta} = \frac{\sin{\theta}}{\cos{\theta}}$$

$$\sin ^2{\theta} + \cos ^2{\theta} = 1$$

$$\tan ^2{\theta} + 1 = \frac{1}{\cos ^2{\theta}}$$

還元公式

余弦定理

$$a^2 = b^2 + c^2 - 2bc\cos{A}$$

$$b^2 = c^2 + a^2 - 2ca\cos{B}$$

$$c^2 = a^2 + b^2 - 2ab\cos{C}$$

加法定理

$$\sin{(\alpha + \beta)} = \sin{\alpha}\cos{\beta} + \cos{\alpha}\sin{\beta}$$

$$\sin{(\alpha - \beta)} = \sin{\alpha}\cos{\beta} - \cos{\alpha}\sin{\beta}$$

$$\cos{(\alpha + \beta)} = \cos{\alpha}\cos{\beta} - \sin{\alpha}\sin{\beta}$$

$$\cos{(\alpha - \beta)} = \cos{\alpha}\cos{\beta} + \sin{\alpha}\sin{\beta}$$

$$\tan{(\alpha + \beta)} = \frac{\tan{\alpha} + \tan{\beta}}{1 - \tan{\alpha}\tan{\beta}}$$

$$\tan{(\alpha - \beta)} = \frac{\tan{\alpha} - \tan{\beta}}{1 + \tan{\alpha}\tan{\beta}}$$

倍角・半角の公式

$$\sin{2\theta} = 2\sin{\theta}\cos{\theta}$$

$$\begin{align*}
\cos{2\theta}
&= \cos ^2{\theta} - \sin ^2{\theta}\\
&= 2\cos ^2{\theta} -1\\
&= 1 - 2\sin ^2{\theta}
\end{align*}$$

$$\tan{2\theta} = \frac{2\tan{\theta}}{1-\tan ^2{\theta}}$$

$$\sin{3\theta} = 3\sin{\theta}-4\sin ^3{\theta}$$

$$\cos{3\theta} = 4\cos ^3{\theta}-3\cos{\theta}$$

$$\tan{3\theta} = \frac{3\tan{\theta}-\tan ^3{\theta}}{1-3\tan ^2{\theta}}$$

$$\sin ^2{\frac{\theta}{2}} = \frac{1-\cos{\theta}}{2}$$

$$\cos ^2{\frac{\theta}{2}} = \frac{1+\cos{\theta}}{2}$$

$$\tan ^2{\frac{\theta}{2}} = \frac{1-\cos{\theta}}{1+\cos{\theta}}$$

積和・和積の公式

合成公式

ただし\(\sin{\alpha} = \frac{b}{\sqrt{a^2 + b^2}}~,~\cos{\alpha} = \frac{a}{\sqrt{a^2 + b^2}}\)

ただし\(\sin{\beta} = \frac{a}{\sqrt{a^2 + b^2}}~,~\cos{\beta} = \frac{b}{\sqrt{a^2 + b^2}}\)

目次に戻る

証明

順番に証明していきます

基本公式

基本公式は定義なので、証明という感じではありません

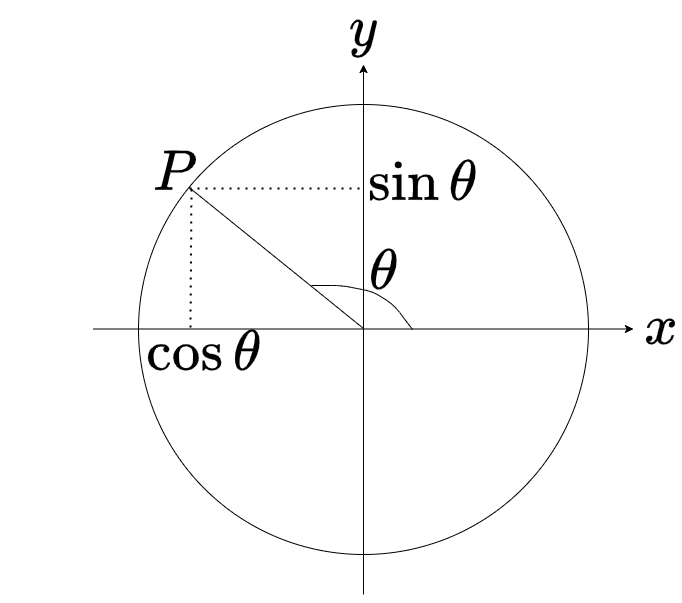
任意の実数\(\theta\)に対して、x軸の正の部分を原点中心として、反時計まわりに\(\theta\)だけ回転させた半直線と単位円の交点の座標を

$$(\cos{\theta}~,~\sin{\theta})$$

と定義します

さらに、\(\color{red}{\tan{\theta} = \frac{\sin{\theta}}{\cos{\theta}}}\)と定義します

単位円なので、三平方の定理より

$$\begin{align*}
x^2 + y^2 &= 1^2\\
\cos ^2{\theta}+\sin ^2{\theta}&=1\\
\color{red}{\sin ^2 \theta + \cos ^2 \theta}&=\color{red}{1}\color{black}{\cdots ①}\\
\end{align*}$$

また、①の両辺を\(\cos ^2\theta\)で割ると

$$\color{red}{\tan ^2\theta + 1 = \frac{1}{\cos ^2\theta}}$$

となります

目次に戻る

還元公式

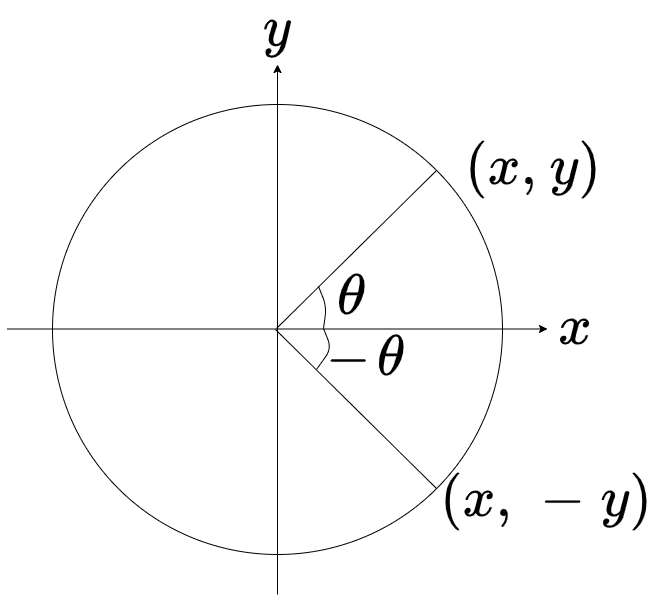
上の図を見ると、x座標は変わらず、y座標の符号が負になっています

よって、x座標であるcosの符号は変わらず、sinの符号だけ負に変わり、それに伴ってtanの符号も負になります

$$\color{red}{\sin{(-\theta)} = -\sin{\theta}~,~\cos{(-\theta)} = \cos{\theta}~,~\tan{(-\theta)} = -\tan{\theta}}$$

となります

上の図の二つの赤色の三角形は合同で、座標はそれぞれ\((x,y)~,~(y,x)\)となります

x座標のcos、y座標のsinが入れ替わるので

$$\color{red}{\sin{(90^{\circ}-\theta)} = \cos{\theta}~,~\cos{(90^{\circ}-\theta)} = \sin{\theta}~,~\tan{(90^{\circ}-\theta)} = \frac{1}{\tan{\theta}}}$$

となります

上の図の二つの赤色の三角形は合同で、座標はそれぞれ\((x,y)~,~(-y,x)\)となります

x座標がcos、y座標がsinであるので

$$\color{red}{\sin{(90^{\circ}+\theta)} = \cos{\theta}~,~\cos{(90^{\circ}+\theta)} = -\sin{\theta}~,~\tan{(90^{\circ}+\theta)} = -\frac{1}{\tan{\theta}}}$$

となります

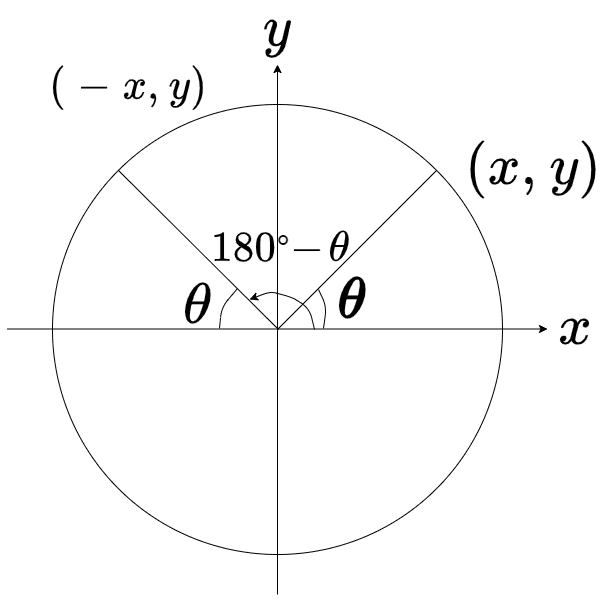
\(\theta と 180^{\circ}-\theta\)の点の位置は、y軸に対して対称であるため、それぞれの座標は

\((x,y)~,~(-x,y)\)となり、x座標の符号が変わります

x座標がcos、y座標がsinであるので

$$\color{red}{\sin{(180^{\circ}-\theta)} = \sin{\theta}~,~\cos{(180^{\circ}-\theta)} = -\cos{\theta}~,~\tan{(180^{\circ}-\theta)} = -\tan{\theta}}$$

となります

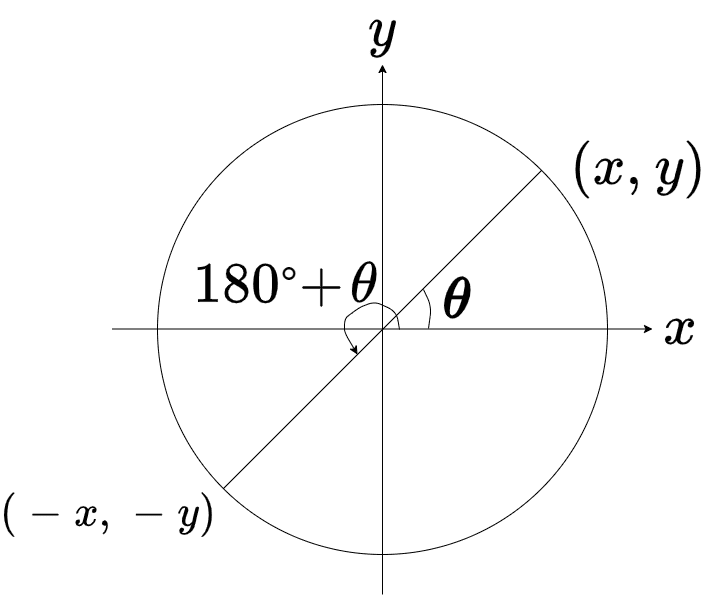
\(\theta と 180^{\circ}+\theta\)の位置関係は、原点対象であるため、それぞれの座標は

\((x,y)~,~(-x,-y)\)と、x , y両方の符号が変わります

よって

$$\color{red}{\sin{(180^{\circ}+\theta)} = -\sin{\theta}~,~\cos{(180^{\circ}+\theta)} = -\cos{\theta}~,~\tan{(180^{\circ}+\theta)} = \tan{\theta}}$$

となります

また、360°回転しても1周回るだけですから、sin,cos,tanに変更はありません

よって

$$\color{red}{\sin{(360^{\circ}+\theta)} = \sin{\theta}~,~\cos{(360^{\circ}+\theta)} = \cos{\theta}~,~\tan{(360^{\circ}+\theta)} = \tan{\theta}}$$

となります

目次に戻る

余弦定理

\(b^2 = c^2 + a^2 - 2ca\cos{B}\)の公式を導出します

１．\(\angle{A}\)が鋭角の場合
２．\(\angle{A}\)が直角の場合
３．\(\angle{A}\)が鈍角の場合

の全ての場合で\(b^2 = c^2 + a^2 - 2ca\cos{B}\)となれば、余弦定理が証明できます

\(\angle{A}\)が鋭角の場合

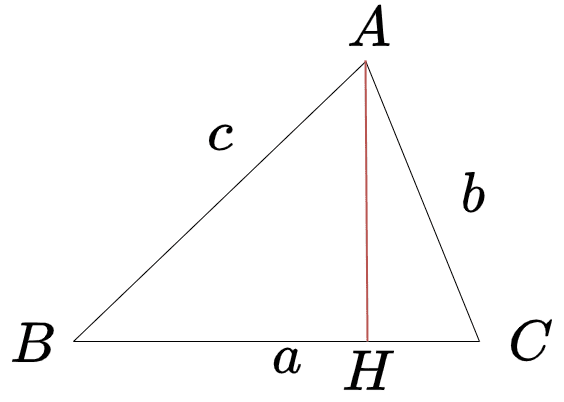
上図のような\(\triangle\)ABCについて考えます

頂点Aから線分BCに垂線を下ろして、交点をHとおきます

\(\triangle{ACH}\)において、三平方の定理より

$$AC^2 = AH^2 + CH^2$$

$$\begin{align*}
b^2
&= (c\cdot \sin{B})^2 + (a - c\cdot \cos{B})^2\\
&= c^2 \sin ^2{B} + a^2 - 2ca\cos{B} + c^2 \cos ^2{B}\\
&= c^2 (\sin ^2{B} + \cos ^2{B}) + a^2 - 2ca\cos{B}\\
&= c^2 + a^2 - 2ca\cos{B}\\
\end{align*}$$

よって

$$\color{red}{b^2 = c^2 + a^2 - 2ca\cos{B}}$$

となります

\(\angle{A}\)が直角の場合

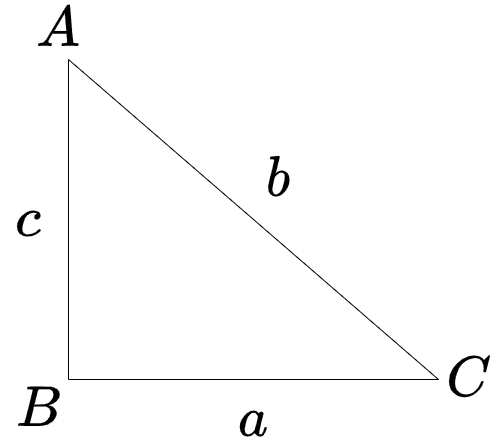
直角の場合、\(\cos{B} = \cos{90^{\circ}} = 0\)になります

\(2ca\cos{B} = 0\)になるから、三平方の定理より

$$\begin{align*}
b^2
&= c^2 + a^2 \\
&= c^2 + a^2 - 2ca\cos{B}
\end{align*}$$

が成り立ちます

よって

$$\color{red}{b^2 = c^2 + a^2 - 2ca\cos{B}}$$

となります

\(\angle{A}\)が鈍角の場合

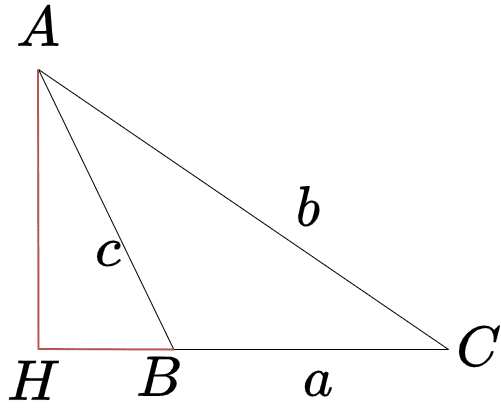
上図のような\(\triangle\)ABCを考えます

頂点Aから線分BCの延長線上に垂線を下ろして、交点をHとします

\(\angle{ABH} = 180^{\circ} - \angle{B}\)であり、還元公式より

$$\sin{(180^{\circ}-\theta)} = \sin{\theta}~,~\cos{(180^{\circ}-\theta)} = -\cos{\theta}$$

が分かっているから

$$\begin{align*}
BH &= c\cdot \cos{(180^{\circ}-B)} = -c\cos{B}\\
AH &= c\cdot \sin{(180^{\circ}-B)} = c\sin{B}
\end{align*}$$

\(\triangle{ACH}\)において、三平方の定理より

$$\begin{align*}
AC^2
&= CH^2 + AH^2\\
&= (BC+BH)^2 + AH^2\\
b^2 &= (a-c\cos{B})^2 + (c\sin{B})^2\\
&= a^2 - 2ca\cos{B} + c^2 \cos ^2{B} + c^2 \sin ^2{B}\\
&= a^2 + c^2 ( \sin ^2{B} + \cos ^2{B}) - 2ca\cos{B}\\
\end{align*}$$

よって

$$\color{red}{b^2 = c^2 + a^2 - 2ca\cos{B}}$$

となります

1,2,3全ての場合で成立したため、余弦定理が証明されました

他の２つ

$$a^2 = b^2 + c^2 - 2bc\cos{A}$$

$$c^2 = a^2 + b^2 - 2ab\cos{C}$$

についても同様に導出できます

目次に戻る

加法定理

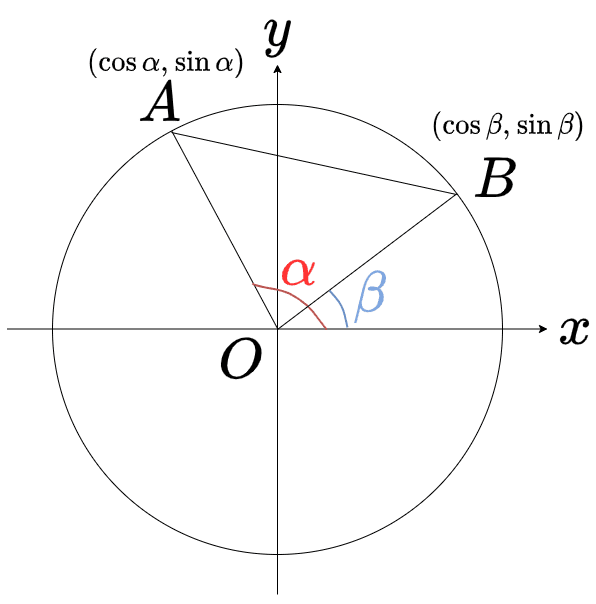
上図のように単位上の点\(A(\cos{\alpha},\cos{\beta})~,~B(\sin{\alpha},\sin{\beta})\)について考えます

距離の公式と、余弦定理を使います

\(\triangle{OAB}\)について、余弦定理より

$$\begin{align*}
AB^2
&= OA^2 + OB^2 - 2OAOB\cos{(\alpha - \beta)}\\
&= 1^2 + 1^2 - 2\cdot 1 \cdot 1\cos{(\alpha - \beta)}\\
&= 2 - 2\cos{(\alpha - \beta)}\cdots ②
\end{align*}$$

また、A,B間の距離の2乗は、距離の公式より

$$\begin{align*}
AB^2
&= (\cos{\alpha} - \cos{\beta})^2+(\sin{\alpha}-\sin{\beta})^2\\
&= \cos ^2{\alpha} - 2\cos{\alpha}\cos{\beta}+\cos ^2{\beta} + \sin ^2{\alpha} - 2\sin{\alpha}\sin{\beta}+\sin ^2{\beta}\\
&= 2 - 2(\cos{\alpha}\cos{\beta}+\sin{\alpha}\sin{\beta})\cdots ③
\end{align*}$$

距離の公式が分からない方は、以下の図で、緑の三角形の三平方の定理を考えてみてください

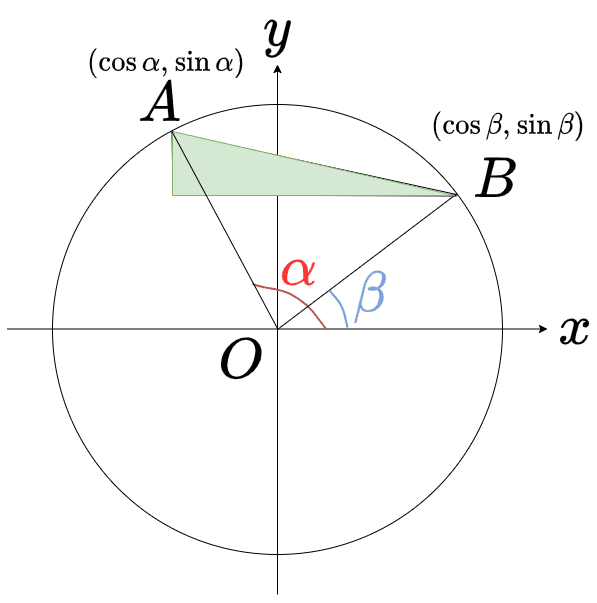
②、③より

$$\begin{align*}
2 - 2(\cos{\alpha}\cos{\beta}+\sin{\alpha}\sin{\beta}) &= 2 - 2\cos{(\alpha - \beta)}\\
\color{red}{\cos{(\alpha - \beta)}} &=\color{red}{ \cos{\alpha}\cos{\beta} + \sin{\alpha}\sin{\beta}}\color{black}{\cdots ④}
\end{align*}$$

となります

④を使って他の式を証明していきます

④の\(\beta\)を\(-\beta\)に置き換えると

$$\cos{(\alpha - (-\beta))} = \cos{\alpha}\cos{(-\beta)}+\sin{\alpha}\sin{(-\beta)}$$

還元公式の

$$\sin{(-\theta)} = -\sin{\theta}~,~\cos{(-\theta)} = \cos{\theta}$$

を使って

$$\color{red}{\cos{(\alpha+\beta)} = \cos{\alpha}\cos{\beta}-\sin{\alpha}\sin{\beta}}\color{black}{\cdots ⑤}$$

となります

④の\(\alpha\)を\(90^{\circ}-\alpha\)に置き換えると

$$\cos{(90^{\circ}-\alpha + \beta)} = \cos{(90^{\circ}-\alpha)}\cos{\beta}-\sin{(90^{\circ}-\alpha)}\sin{\beta}$$

還元公式の

$$\sin{(90^{\circ}-\theta)} = \cos{\theta}~,~\cos{(90^{\circ}-\theta)} = \sin{\theta}$$

を使って

$$\begin{align*}
\cos{\{90^{\circ}-(\alpha - \beta)\}} &= \cos{(90^{\circ}-\alpha)}\cos{\beta}-\sin{(90^{\circ}-\alpha)}\sin{\beta}\\
\color{red}{\sin{(\alpha - \beta)}} &= \color{red}{\sin{\alpha}\cos{\beta}-\cos{\alpha}\sin{\beta}}\color{black}{\cdots ⑥}
\end{align*}$$

となります

⑥の\(\beta\)を\(-\beta\)に置き換えると

$$\sin{(\alpha + \beta)} = \sin{\alpha}\cos{(-\beta)}-\cos{\alpha}\sin{(-\beta)}$$

還元公式の

$$\sin{(-\theta)} = -\sin{\theta}~,~\cos{(-\theta)} = \cos{\theta}$$

を使って

$$\color{red}{\sin{(\alpha + \beta)} = \sin{\alpha}\cos{\beta}+\cos{\alpha}\sin{\beta}}\color{black}{\cdots ⑦}$$

となります

⑤、⑦より

$$\begin{align*}
\tan{(\alpha + \beta)}
&= \frac{\sin{(\alpha + \beta)}}{\cos{(\alpha + \beta)}}\\
&= \frac{\sin{\alpha}\cos{\beta}+\cos{\alpha}\sin{\beta}}{\cos{\alpha}\cos{\beta}-\sin{\alpha}\sin{\beta}}\\
&= \frac{\tan{\alpha}+\tan{\beta}}{1-\tan{\alpha}\tan{\beta}}
\end{align*}$$

よって

$$\color{red}{\tan{(\alpha + \beta)} = \frac{\tan{\alpha} + \tan{\beta}}{1-\tan{\alpha}\tan{\beta}}}\color{black}{\cdots ⑧}$$

⑧の\(\beta\)を\(-\beta\)に置き換えると

$$\tan{(\alpha - \beta)} = \frac{\tan{\alpha}+\tan{(-\beta)}}{1-\tan{\alpha}\tan{(-\beta)}}$$

還元公式の\(\tan{(-\theta)} = -\tan{\theta}\)を使って

$$\color{red}{\tan{(\alpha - \beta)} = \frac{\tan{\alpha} - \tan{\beta}}{1 + \tan{\alpha}\tan{\beta}}}$$

となります

目次に戻る

半角・倍角の公式

加法定理を使って求めていきます

2倍角の公式

まずは2倍角の公式から

$$\begin{align*}
\color{red}{\sin{2\theta}}\color{black}
&=\sin{(\theta + \theta)}\\
&= \sin{\theta}\cos{\theta} + \cos{\theta}\sin{\theta}\\
&= \color{red}{2\sin{\theta}\cos{\theta}}
\end{align*}$$

$$\begin{align*}
\cos{2\theta}
&= \cos{(\theta + \theta)}\\
&= \cos{\theta}\cos{\theta} - \sin{\theta}\sin{\theta}\\
&= \cos ^2{\theta} - \sin ^2{\theta}
\end{align*}$$

基本公式\(\sin ^2{\theta} + \cos ^2{\theta} = 1\)より

$$\begin{align*}
\color{red}{\cos{2\theta}}
&= \color{red}{\cos ^2{\theta} - \sin ^2{\theta}}\\
&= \color{red}{2\cos ^2{\theta} -1}\\
&= \color{red}{1 - 2\sin ^2{\theta}}
\end{align*}$$

$$\begin{align*}
\color{red}{\tan{2\theta}}
&=\tan{\theta + \theta}\\
&= \frac{\tan{\theta}+\tan{\theta}}{1-\tan{\theta}\cdot\tan{\theta}}\\
&=\color{red}{\frac{2\tan{\theta}}{1-\tan ^2{\theta}}}
\end{align*}$$

半角の公式

半角の公式は2倍角の公式の\(\cos{2\theta}\)を利用すれば導出することができます

$$\begin{align*}
\cos{2\theta} &= 1-2\sin ^2{\theta}\\
2\sin ^2{\theta} &= 1 - \cos{2\theta}\\
\sin ^2{\theta} &= \frac{1 - \cos{2\theta}}{2}\cdots⑨\\
\end{align*}$$

⑨の\(\theta\)を\(\frac{\theta}{2}\)に置き換えると

$$\color{red}{\sin ^2{\frac{\theta}{2}} = \frac{1-\cos{\theta}}{2}}$$

$$\begin{align*}
\cos{2\theta} &= 2\cos ^2{\theta} - 1\\
2\cos ^2{\theta} &= 1 + \cos{2\theta}\\
\cos ^2{\theta} &= \frac{1+\cos{2\theta}}{2}\cdots⑩
\end{align*}$$

⑩の\(\theta\)を\(\frac{\theta}{2}\)に置き換えると

$$\color{red}{\cos ^2{\frac{\theta}{2}} = \frac{1+\cos{\theta}}{2}}$$

よって

$$\begin{align*}
\color{red}{\tan ^2{\frac{\theta}{2}}}\color{black}
&= \frac{\sin ^2{\frac{\theta}{2}}}{\cos ^2{\frac{\theta}{2}}}\\
&=\color{red}{\frac{1-\cos{\theta}}{1+\cos{\theta}}}
\end{align*}$$

3倍角の公式

3倍角の公式は、2倍角の公式と加法定理より証明できます

$$\begin{align*}
\color{red}{\sin{3\theta}}\color{black}
&=\sin{(\theta + 2\theta)}\\
&= \sin{\theta}\cos{2\theta}+\cos{\theta}\sin{2\theta}\\
&= \sin{\theta}(1-2\sin ^2{\theta})+ 2\sin{\theta}\cos ^2{\theta}\\
&= \sin{\theta}(1-2\sin ^2{\theta})+ 2\sin{\theta}(1-\sin ^2{\theta})\\
&= \color{red}{3\sin{\theta}-4\sin ^3{\theta}}
\end{align*}$$

$$\begin{align*}
\color{red}{\cos{3\theta}}\color{black}
&= \cos{(\theta + 2\theta)}\\
&= \cos{\theta}\cos{2\theta} - \sin{\theta}\sin{2\theta}\\
&= \cos{\theta}(2\cos ^2{\theta} - 1) - 2\sin ^2{\theta}\cos{\theta}\\
&= \cos{\theta}(2\cos ^2{\theta} -1) - 2(1 - \cos ^2{\theta})\cos{\theta}\\
&= \color{red}{4\cos ^3{\theta} - 3\cos{\theta}}
\end{align*}$$

$$\begin{align*}
\color{red}{\tan{3\theta}}\color{black}
&= \tan{(2\theta + \theta)}\\
&= \frac{\tan{2\theta}+\tan{\theta}}{1-\tan{2\theta}\tan{\theta}}\\
&=\frac{\frac{2\tan{\theta}}{1-\tan ^2{\theta}}+\tan{\theta}}{1-\frac{2\tan{2\theta}}{1-\tan ^2{\theta}}}\\
&= \frac{2\tan{\theta}+\tan{\theta}-\tan ^3{\theta}}{1-\tan ^2{\theta}-2\tan{\theta}}\\
&= \color{red}{\frac{3\tan{\theta}-\tan ^3{\theta}}{1-3\tan ^2{\theta}}}
\end{align*}$$

目次に戻る

積和・和積の公式

積和・和積の公式は、加法定理を用いて導出します

積和の公式

$$\begin{array}{rr}
& \sin{(\alpha + \beta)} = \sin{\alpha}\cos{\beta} + \cos{\alpha}\sin{\beta}\\
+\big{)}&\sin{(\alpha - \beta)} = \sin{\alpha}\cos{\beta} - \cos{\alpha}\sin{\beta}\\
\hline
&\sin{(\alpha + \beta)} + \sin{(\alpha - \beta)} = 2\sin{\alpha}\cos{\beta}\cdots⑪
\end{array}$$

よって

$$\color{red}{\sin{\alpha}\cos{\beta} =\frac{1}{2}\{\sin{(\alpha + \beta)} + \sin{(\alpha - \beta)}\}}$$

$$\begin{array}{rr}
& \sin{(\alpha + \beta)} = \sin{\alpha}\cos{\beta} + \cos{\alpha}\sin{\beta}\\
-\big{)}&\sin{(\alpha - \beta)} = \sin{\alpha}\cos{\beta} - \cos{\alpha}\sin{\beta}\\
\hline
&\sin{(\alpha + \beta)} - \sin{(\alpha - \beta)} = 2\sin{\alpha}\cos{\beta}\cdots⑫
\end{array}$$

よって

$$\color{red}{\sin{\alpha}\cos{\beta} =\frac{1}{2}\{\sin{(\alpha + \beta)} - \sin{(\alpha - \beta)}\}}$$

同様に

$$\begin{array}{rr}
& \cos{(\alpha + \beta)} = \cos{\alpha}\cos{\beta} - \sin{\alpha}\sin{\beta}\\
+\big{)}&\sin{(\alpha - \beta)} = \cos{\alpha}\cos{\beta} + \sin{\alpha}\sin{\beta}\\
\hline
&\cos{(\alpha + \beta)} + \cos{(\alpha - \beta)} = 2\cos{\alpha}\cos{\beta}\cdots⑬
\end{array}$$

よって

$$\color{red}{\cos{\alpha}\cos{\beta} = \frac{1}{2}\cos{(\alpha + \beta)}+\cos{(\alpha - \beta)}}$$

$$\begin{array}{rr}
& \cos{(\alpha + \beta)} = \cos{\alpha}\cos{\beta} - \sin{\alpha}\sin{\beta}\\
-\big{)}&\sin{(\alpha - \beta)} = \cos{\alpha}\cos{\beta} + \sin{\alpha}\sin{\beta}\\
\hline
&\cos{(\alpha + \beta)} - \cos{(\alpha - \beta)} = -2\sin{\alpha}\sin{\beta}\cdots⑭
\end{array}$$

よって

$$\color{red}{\cos{\alpha}\cos{\beta} = -\frac{1}{2}\cos{(\alpha + \beta)}-\cos{(\alpha - \beta)}}$$

和積の公式

\(\alpha + \beta = A~,~\alpha - \beta = B\)とおくと

\(\alpha = \frac{A+B}{2}~,~\beta = \frac{A-B}{2}\)であるから

⑪、⑫、⑬、⑭に代入して

$$\color{red}{\sin{A}+\sin{B} = 2\sin{\frac{A+B}{2}}\cos{\frac{A-B}{2}}}$$

$$\color{red}{\sin{A}-\sin{B} = 2\cos{\frac{A+B}{2}}\sin{\frac{A-B}{2}}}$$

$$\color{red}{\sin{A}+\sin{B} = 2\cos{\frac{A+B}{2}}\cos{\frac{A-B}{2}}}$$

$$\color{red}{\sin{A}+\sin{B} = 2\sin{\frac{A+B}{2}}\sin{\frac{A-B}{2}}}$$

目次に戻る

合成公式

合成公式の導出にも、加法定理を使用します

sinの合成公式

上図のように、点\(P(a,b)\)をとり、原点からの長さを\(r\)とします

$$r = \sqrt{a^2 + b^2}~,~a = r\cos{\alpha}~,~b = r\sin{\alpha}\cdots ⑮$$

であるから

$$\begin{align*}
\color{red}{a\sin{\theta} + b\cos{\theta}}\color{black}
&= r\cos{\alpha}\sin{\theta}+r\sin{\alpha}\cos{\theta}\\
&= r(\sin{\theta}\cos{\alpha}+\cos{\theta}\sin{\alpha})\\
&= \color{red}{\sqrt{a^2 + b^2}\sin{(\theta + \alpha)}}
\end{align*}$$

ただし、⑮より

$$\color{red}{\sin{\alpha}=\frac{b}{\sqrt{a^2 + b^2}}~,~\cos{\alpha}=\frac{a}{\sqrt{a^2 + b^2}}}$$

cosの合成公式

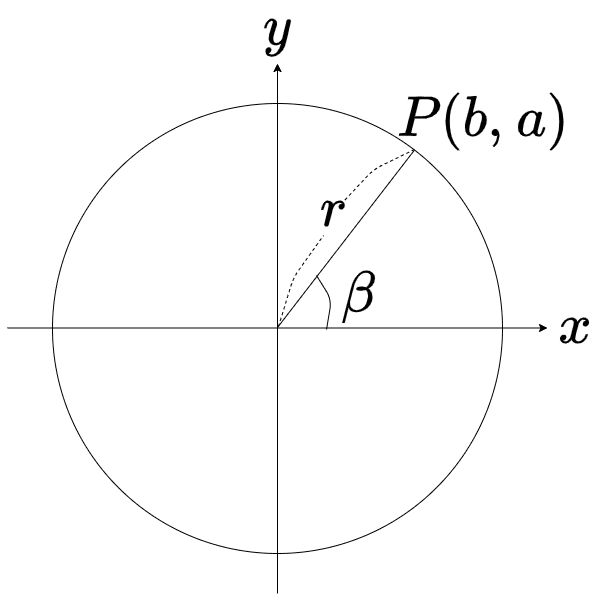
上図のように、点\(P(b,a)\)をとり、原点からの長さを\(r\)とします

$$r = \sqrt{a^2 + b^2}~,~b = r\cos{\beta}~,~a = r\sin{\beta}\cdots ⑯$$

であるから

$$\begin{align*}
\color{red}{a\sin{\theta}+b\cos{\theta}}\color{black}
&= b\cos{\theta}+a\sin{\theta}\\
&= r\cos{\beta}\cos{\theta} + r\sin{\beta}\sin{\theta}\\
&=r(\cos{\theta}\cos{\beta}+\sin{\theta}\sin{\beta})\\
&= \color{red}{\sqrt{a^2+b^2}\cos{(\theta - \beta)}}
\end{align*}$$

ただし、⑯より

$$\color{red}{\sin{\alpha}=\frac{b}{\sqrt{a^2 + b^2}}~,~\cos{\alpha}=\frac{a}{\sqrt{a^2 + b^2}}}$$

目次に戻る

このサイトを辞書のように使う方法

ここまで全ての公式と導出方法を書いてきましたが、一回見ただけでは覚えられないと思います

1タップでこのページに飛べるための方法を書いていきます

iPhoneの場合

１．Safariでこのページを表示
２．画面下部の 共有アイコン（四角から矢印が飛び出したマーク）をタップ
３．「ホーム画面に追加」をタップ

Androidの場合

１．Google Chromeでこのページを表示
２．画面右上の メニューアイコン（縦に並んだ3つの点）をタップ
３．「ホーム画面に追加」をタップ
４．タイトルの変更をして(各自自由に)、「追加」をタップ

これでアイコンがホーム画面上に追加されます

アイコンをタップすることで、このページに直接アクセスでき、後から確認するときに便利です

ぜひやってみてください

最後までお読みいただきありがとうございました！

目次に戻る

【参考】
https://rikeilabo.com/sine-cosine-theorem
https://atarimae.biz/archives/18041
https://mathtrain.jp/trig_basic
https://rikeilabo.com/trigonometric-addition-formulas