伝達関数とは？

2021年2月25日

この記事では、制御工学で重要な項目である伝達関数について説明します

伝達関数とは

制御工学では、扱いたいシステムに入力信号を与えて出力信号を見るということをしますが、ほとんどの場合、入力信号がいつも同じではありません

そのときに入力と出力の関係を一意に表せるようなものがあればとても便利です

そして、その入力と出力の関係を表せるものが伝達関数です

制御系が定常状態で、すべての初期値を0とおいたとき、ラプラス変換された出力信号に対する入力信号の比を伝達関数と呼びます

一般的に、伝達関数はG(s)で表され、システムへの入力信号のラプラス変換を$U(s)$、出力信号のラプラス変換を$Y(s)$とすると

$$G(s) = \frac{Y(s)}{U(s)} = \frac{\mathcal{L}[y(t)]}{\mathcal{L}[u(t)]}$$

のように表されます

動的システムの特性は微分方程式で表されるため、古典制御工学では微分方程式から伝達関数を導出することが求められます

例として、以下のようなマス・バネ・ダンパシステムについて考えます

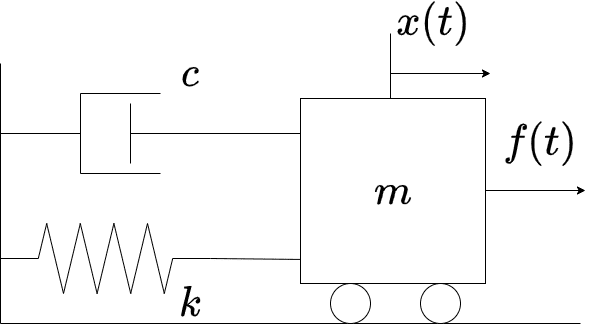
質量mの物体にバネとダンパが並列に接続されていて、物体は水平に移動できます

$m$は質量、$c$は粘性抵抗係数、$k$はバネ定数、$f(t)$は物体に加える力、$x(t)$は変位、$x'(t)$は速度、$x''(t)$は加速度とすると、マス・バネ・ダンパシステム運動方程式は

$$mx''(t) + cx'(t) + kx(t) = f(t)$$

のようになります

初期値を0として、この微分方程式をラプラス変換すると

$$\begin{align*}
ms^{2}X(s) + csX(s) + kX(s) &= F(s)\\
(ms^2 + cs + k)X(s) &= F(s)\\
\frac{X(s)}{F(s)} = \frac{1}{ms^2 + cs + k}
\end{align*}$$

のようになるので、このマス・バネ・ダンパシステムの伝達関数は

$$G(s) = \frac{X(s)}{F(s)} = \frac{1}{ms^2 + cs + k}\cdots ①$$

と、導出できました

伝達関数のメリットは、システムの統合が簡単になるというところです

例えば、先ほどのマス・バネ・ダンパシステムに部品Aを付けるとします

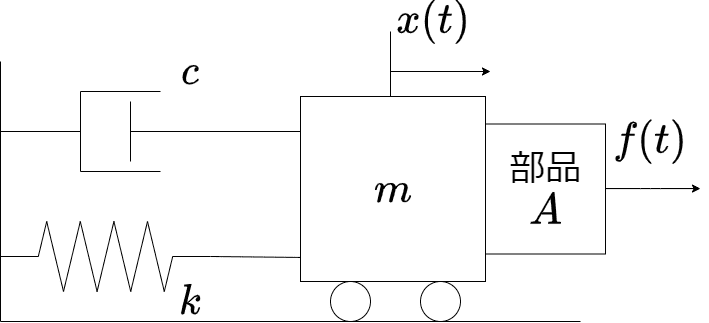
この部品Aは電流$i(t)$の入力によって、力$f(t)$を出力するものして、運動方程式が以下のようなものであるとします

$$f''(t) + a_{1}f'(t) + a_{2}f(t) = i(t)$$

部品Aの伝達関数$G_{A}(s)$は、先ほどと同じように計算すると

$$G_{A}(s) = \frac{F(s)}{I(s)} = \frac{1}{s^2 + a_{1}s + a_{2}}\cdots ②$$

のようになります

①、②より

$$X(s) = \frac{1}{ms^2 + cs + k}\cdot\frac{1}{s^2 + a_{1}s + a_{2}}I(s)$$

となります

電気系モデル(部品A)と、機械系モデル(マス・バネ・ダンパシステム)の複合システムの複雑な微分方程式を統合することができています

このように、伝達関数を使うことで異なる分野から構成されるシステムであっても、シンプルに考えることができます