この記事では、一次遅れ系に対するインパルス応答とインディシャル応答(単位ステップ応答)について解説していきます
一次遅れ要素の伝達関数
制御系のある要素に入力信号を加えたとき、入力信号の位相に対して、出力信号の位相が遅れるような要素を遅れ要素と呼びます
遅れ要素の中でも、伝達関数の分母がsの一次式で表されるものを一次遅れ要素と呼びます
一次遅れ要素の伝達関数は一般に以下のような形で表されます
$$G(s) = \frac{K}{1 + Ts}$$
\(K , T\)はそれぞれ、比例ゲイン、時定数と呼びます
一次遅れ系のインパルス応答
インパルス入力\(u(t)\)のラプラス変換\(U(s)\)は
$$U(s) = \mathcal{L}[u(t)] = 1$$
であるから、一次遅れ系のインパルス応答\(y(t)\)は
$$\begin{align*}
y(t)
&= \mathcal{L}^{-1}[G(s)U(s)]\\
&= \mathcal{L}^{-1}[G(s)\cdot 1]\\
&= \mathcal{L}^{-1}[\frac{K}{1 + Ts}]\\
&= \mathcal{L}^{-1}[\frac{\frac{K}{T}}{\frac{1}{T}+s}]\\
&= \frac{K}{T}\mathcal{L}^{-1}[\frac{1}{\frac{1}{T}+s}]\\
&= \frac{K}{T}\mathcal{L}^{-1}[\frac{1}{s+\frac{1}{T}}]\\
&= \frac{K}{T}e^{-\frac{1}{T}t}\cdots ①
\end{align*}$$
のようになります
①から、初期値\(y(0) = \frac{K}{T}\)と最終値\(\lim_{t \to \infty}y(t) = 0\)であることが分かります
\(T=K\)としてグラフにすると
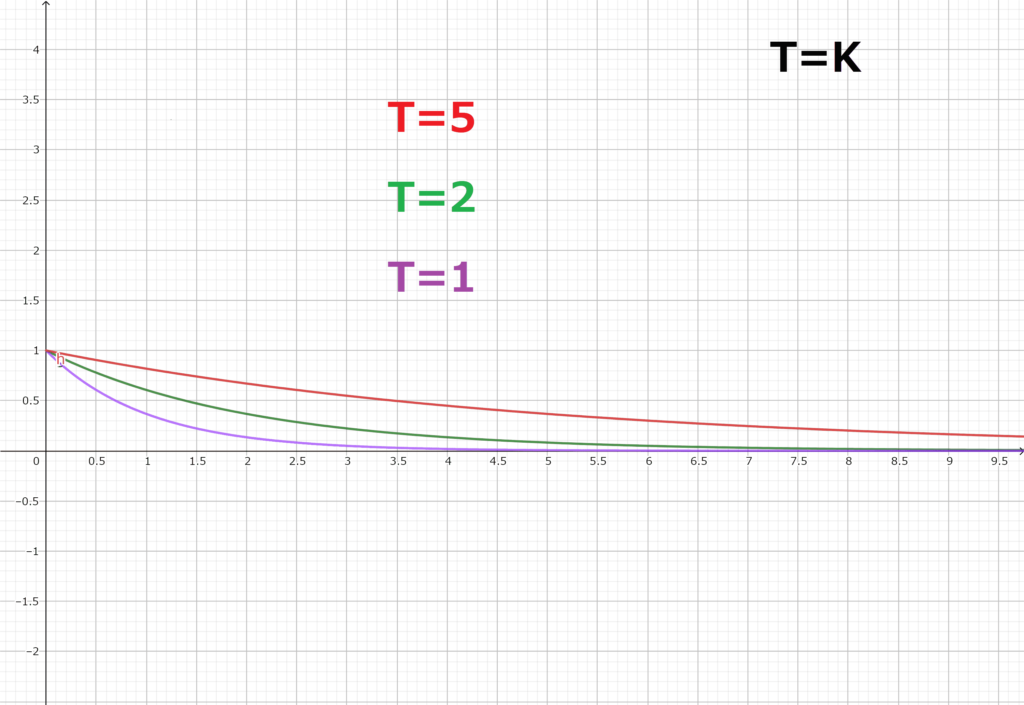
のようになります
\(T\)の値が大きくなるにつれて、定常値0に収束するまでの時間が多く必要になっていることが分かりますね
一次遅れ系のインディシャル(単位ステップ)応答
単位ステップ入力\(u(t)\)のラプラス変換\(U(s)\)は
$$U(s) = \mathcal{L}[u(t)] = \frac{1}{s}$$
であるから、一次遅れ系のインディシャル応答\(y(t)\)は
$$\begin{align*}
y(t)
&= \mathcal{L}^{-1}[G(s)U(s)]\\
&= \mathcal{L}^{-1}[\frac{K}{1 + Ts}\cdot \frac{1}{s}]\\
&= \mathcal{L}^{-1}[\frac{K}{s(Ts+1)}]\\
&= K\mathcal{L}^{-1}[\frac{1}{s}-\frac{T}{Ts+1}]\\
&= K\mathcal{L}^{-1}[\frac{1}{s}-\frac{1}{s+\frac{1}{T}}]\\
&= K(1-e^{-\frac{1}{T}t})\cdots ②
\end{align*}$$
のようになります
②から初期値\(y(0) = 0\)と最終値\(\lim_{t \to \infty}y(t) = K\)であることが分かります
\(K=1\)としてグラフにすると
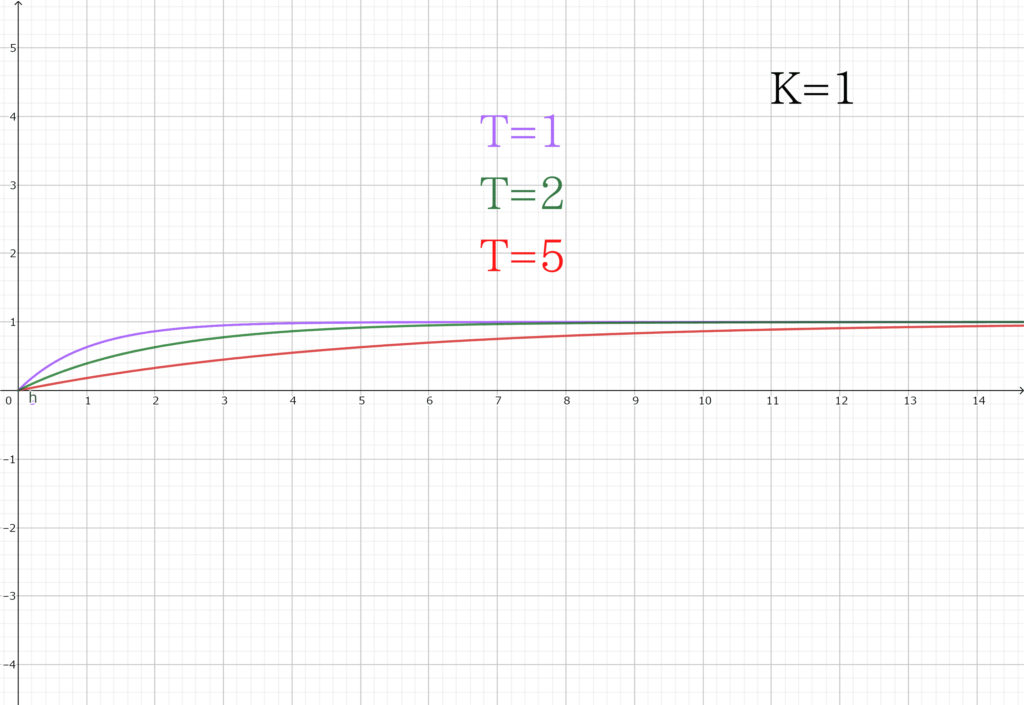
のようになります
\(T\)の値が大きくなるにつれて、定常値\(K\)に収束するまでの時間が多く必要になっていることが分かりますね
一次遅れ系の安定性
一次遅れ系は時定数\(T\)に注目する
一次遅れ系のインパルス応答、インディシャル応答はそれぞれ
$$\frac{K}{T}e^{-\frac{1}{T}t}~,~K(1-e^{-\frac{1}{T}t})$$
のようになっており、時定数\(T\)の値によって速応性が決まります
時定数\(T\)が正である場合は、値が大きいほど収束するまでの時間が短くなり、時定数\(T\)が負である場合は発散します
安定性
制御系が安定であるための条件として、伝達関数\(G(s)\)の「分母多項式=0」の解の実部が負であるというものがあります
一次遅れ系であれば伝達関数の分母多項式は\(1+Ts\)であるから、「分母多項式=0」の解は
$$s = -\frac{1}{T}$$
となります
先ほど述べた、時定数\(T\)が正である場合は、値が大きいほど収束するまでの時間が短くなり、時定数\(T\)が負である場合は発散しますというのは、伝達関数の「分母多項式=0」の解が負であれば安定、正であれば不安定、と同じことであるのが分かると思います
これは、一次遅れ系以外でも当てはまりますし、重要な考え方なのでぜひ覚えておいてください
まとめ
一次遅れ要素の伝達関数は
$$G(s) = \frac{K}{1 + Ts}$$
一次遅れ系のインパルス応答は
$$\frac{K}{T}e^{-\frac{1}{T}t}$$
一次遅れ系のインディシャル応答は
$$K(1-e^{-\frac{1}{T}t})$$
となります
時定数\(T\)が正であれば、安定となります