今回の導出方法では、三角形と平行四辺形の断面二次モーメントの公式を使用します
これらについては、断面二次モーメントの公式一覧をご覧ください
以下のような斜めになった長方形の断面二次モーメントを求めます
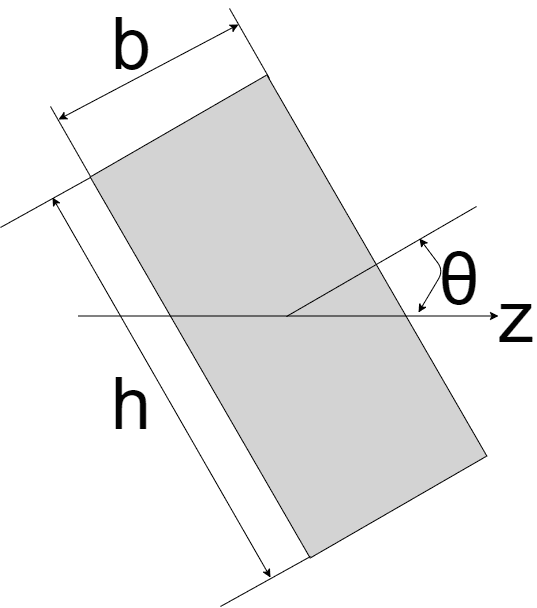
断面二次モーメントを求めるために、以下のように補助線を書き加えます
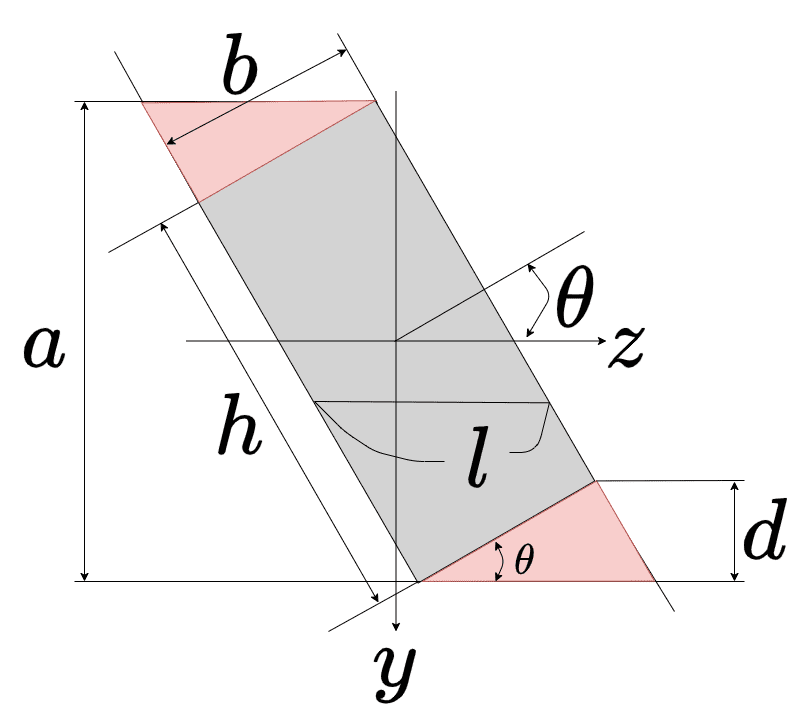
長方形+2つの三角形を合わせた、平行四辺形の断面二次モーメント\(I_{p}\)から、2つの三角形の断面二次モーメント\(2I_{t}\)を引くというやり方で求めていきます
まずは、a , d , lを求めます
\(d = b\sin{\theta}~,~l = \frac{b}{\cos{\theta}}~,~a = b\sin{\theta}+h\cos{\theta}\)
となります
長方形+2つの三角形を合わせた、z軸まわりの平行四辺形の断面二次モーメントは、断面二次モーメントの公式一覧より
$$I_{p} = \frac{la^3}{12}$$
となります
また、三角形の重心を通る軸まわりの断面二次モーメントは、断面二次モーメントの公式一覧より
$$I_{t'} = \frac{ld^3}{36}$$
z軸まわりの断面二次モーメントで考えると、平行軸の定理より
$$\begin{align*}
I_{t}
&= I_{t'} + Ad^2\\
&= \frac{ld^3}{36} + \frac{ld}{2} \cdot (\frac{a}{2} - \frac{d}{3})^2\\
&= \frac{l}{36}\{d^3 + \frac{d}{2}(3a - 2d)^2\}\\
&= \frac{l}{36}(d^3 + \frac{9}{2}a^{2}d-6ad^2 + 2d^3)\\
&= \frac{l}{12}(d^3 + \frac{3}{2}a^{2}d - 2ad^2)
\end{align*}$$
よってz軸まわりの断面二次モーメントは
$$\begin{align*}
I_{z}
&= I_{p} - 2I_{t}\\
&= \frac{la^{3}}{12} - \frac{l}{12}(2d^3 + 3a^{2}d - 4ad^2)\\
&= \frac{l}{12}\{ (b\sin{\theta}+h\cos{\theta})^3 - 2b^{3}\sin ^3 \theta - 3b\sin{\theta}(b\sin{\theta} + h\cos{\theta})^2\\
&~~~~~~+4b^2\sin ^2 \theta(b\sin{\theta}+h\cos{\theta})\}\\
&= \frac{l}{12}(\color{red}{b^{3}\sin ^3 \theta} \color{black}{+} \color{blue}{3bh^2\sin{\theta}\cos ^2 \theta} \color{black}{+}\color{magenta}{3b^{2}h\sin ^2 \theta \cos{\theta}} \color{black}{+} \color{green}{h^3 \cos ^3 \theta}\\
&~~~~~~- \color{red}{2b^3 \sin ^3 \theta}\color{black}{-}\color{red}{3b^3 \sin ^3 \theta} \color{black}{-} \color{magenta}{6b^2 h \sin ^2 \theta \cos{\theta}} \color{black}{-} \color{blue}{3bh^2 \sin{\theta}\cos ^2 \theta}\\
&~~~~~~+\color{red}{4b^3 \sin ^2 \theta} \color{black}{+} \color{magenta}{4b^2 h \sin{\theta}\cos{\theta})}\\
&= \frac{b}{12\cos{\theta}}(\color{magenta}{b^2 h \sin ^3 \theta \cos{\theta}} \color{black}{+} \color{green}{h^3 \cos ^3 \theta})
\end{align*}$$
I_{z}
&= I_{p} - 2I_{t}\\
&= \frac{la^{3}}{12} - \frac{l}{12}(2d^3 + 3a^{2}d - 4ad^2)\\
&= \frac{l}{12}\{ (b\sin{\theta}+h\cos{\theta})^3 - 2b^{3}\sin ^3 \theta - 3b\sin{\theta}(b\sin{\theta} + h\cos{\theta})^2\\
&~~~~~~+4b^2\sin ^2 \theta(b\sin{\theta}+h\cos{\theta})\}\\
&= \frac{l}{12}(\color{red}{b^{3}\sin ^3 \theta} \color{black}{+} \color{blue}{3bh^2\sin{\theta}\cos ^2 \theta} \color{black}{+}\color{magenta}{3b^{2}h\sin ^2 \theta \cos{\theta}} \color{black}{+} \color{green}{h^3 \cos ^3 \theta}\\
&~~~~~~- \color{red}{2b^3 \sin ^3 \theta}\color{black}{-}\color{red}{3b^3 \sin ^3 \theta} \color{black}{-} \color{magenta}{6b^2 h \sin ^2 \theta \cos{\theta}} \color{black}{-} \color{blue}{3bh^2 \sin{\theta}\cos ^2 \theta}\\
&~~~~~~+\color{red}{4b^3 \sin ^2 \theta} \color{black}{+} \color{magenta}{4b^2 h \sin{\theta}\cos{\theta})}\\
&= \frac{b}{12\cos{\theta}}(\color{magenta}{b^2 h \sin ^3 \theta \cos{\theta}} \color{black}{+} \color{green}{h^3 \cos ^3 \theta})
\end{align*}$$
と、求められます