この記事では、システムの時間応答の性能評価について説明します
過渡応答・定常応答について
システムにおいて、入力の変化に対する出力の変化を、時間応答と呼びます
制御対象の時間応答は、以下の二つに分類されます
過渡応答・・・観測からあまり時間が経過しておらず、状態が安定していない応答
定常応答・・・ある程度の時間が経過して状態が安定した応答
下の図は、あるシステムのインディシャル応答(単位ステップ応答)を表した図です
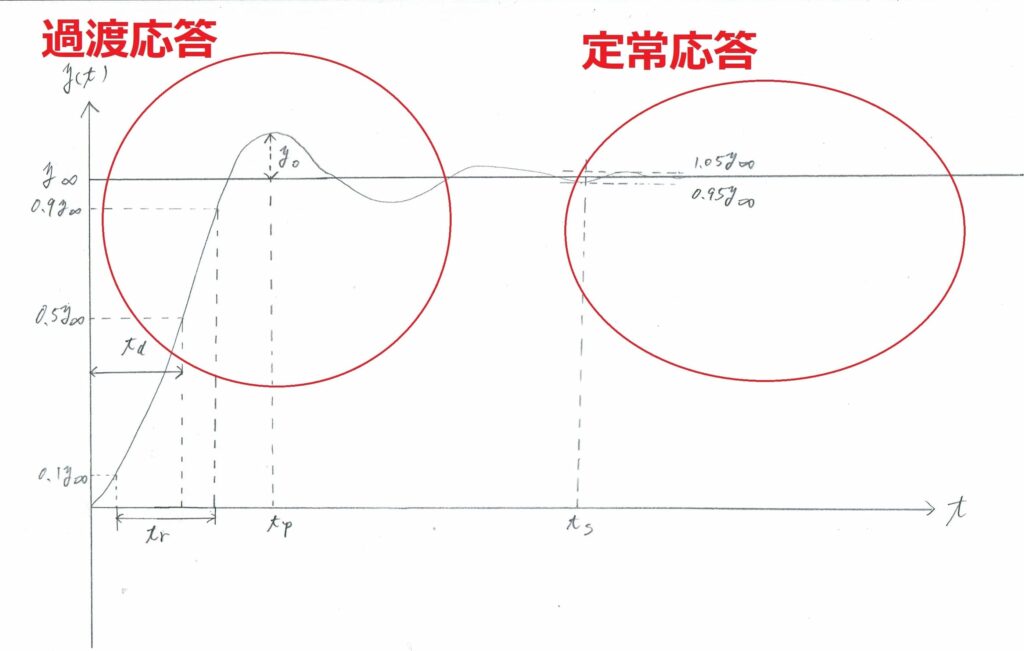
過渡応答と定常応答のそれぞれの特性を過渡特性、定常特性と呼びます
過渡特性
観測を始めてすぐは、出力(制御量)が安定していない状態(過渡状態)になります
この状態ではシステムが正常に動作しないため、出力(制御量)をできるだけ速やかに目標値に近づけることが求められます
過渡特性の評価は「速応性」と「安定性」について行われます
速応性・・・制御対象の出力と目標値の差(偏差)をどれだけ速やかに減らせるか
安定性・・・制御量が安定するまでのオーバーシュート(行き過ぎ量)がどれだけ小さいか
速応性、安定性に優れているシステムが、良いシステムだということになります
過渡特性を評価する指標として、以下のようなものがあります
| 特性値 | 記号 | 説明 | 評価 |
| 定常値 | $$y_{\infty}$$ | 最終的に収束する値 | |
| 遅れ時間(遅延時間) | $$t_{d}$$ | 目標値の50%になるまでの時間 | 速応性 |
| 立ち上がり時間 | $$t_{r}$$ | 定常値の10%から90%になるまでの時間 | 速応性 |
| 行き過ぎ時間 | $$t_{p}$$ | 初期値0から\(y_{\infty}\)になるまでの時間 | 速応性 |
| 整定時間 | $$t_{s}$$ | 定常値の±5%の範囲で安定するまでの時間 | 安定性・速応性 |
| 行き過ぎ量(オーバーシュート) | $$y_{O}$$ | 目標値を超えた最大値 $$y_{O} = \frac{y_{max} - y_{\infty}}{y_{\infty}} \times 100%$$ | 安定性 |
定常特性
観測を始めて十分時間が経過し、安定な状態のことを定常状態と呼びます
そして、定常状態の特性を定常特性と呼びます
定常特性の評価は、「偏差量(定常偏差)」によって行います
定常偏差、つまり制御量と目標値の差が小さいほど、良いシステムだということになります
定常偏差\(e(t)\)は、目標値\(r(t)\)と制御量\(c(t)\)とすると、以下の式で求められます
$$\lim_{ t \to \infty } e(t) = \lim_{ t \to \infty } \{ r(t) - c(t) \}$$
$$\lim_{ t \to \infty } e(t) = \lim_{ s \to 0 } sE(s) = \lim_{ s \to 0 } \{ R(s) - C(s) \} \cdots ①$$
①は最終値定理を使った変形です