説明のために公式一覧のページと一部文字を変更しています
以下のような三角形の断面二次モーメントについて考えます
z軸は図心を通り、底辺に平行な軸です

z'軸からyだけ離れたところの微少距離dyを考える
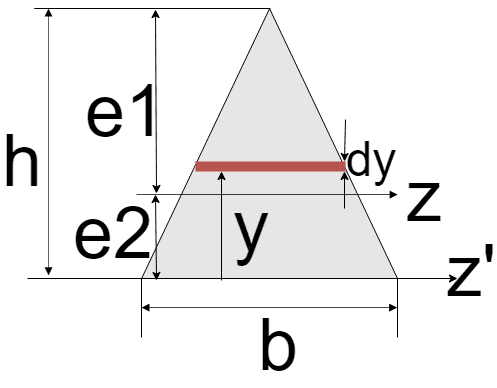
ここで、赤い微少部分の微少面積dAは近似的に長方形です
長方形の短辺はdyであり、長辺は三角形の高さによって異なります
長辺はz'軸からの距離に対して反比例しますので
$$z' = py + q~~~(p,qは定数)$$
とおいて考えます
長辺の長さは、z'軸からの距離が0のときにb、z'軸からの距離がhのときに0であるため、代入すると
$$b = q~,~0=ph+q$$
より
$$p = -\frac{q}{h}~,~q = b$$
となるから、長辺の長さは
$$z' = \frac{b(h-y)}{h}$$
となります
微少部分の面積dAは長辺×短辺で表されるので
$$dA = \frac{b(h - y)}{h}dy$$
となります
z'軸まわりの断面二次モーメントは
$$\begin{align*}
I_{z'}
&= \int _A y^2 dA\\
&= \int_{0}^{h}y^2 \cdot \frac{b(h-y)}{h} dy \\
&= \frac{b}{h}\int_{0}^{h} (y^2 h - y^3)dy \\
&= \frac{b}{h}\left[ \frac{y^3}{3}h - \frac{y^4}{4} \right]_{0}^{h}\\
&= \frac{bh^3}{12}
\end{align*}$$
と、求められます
ここで、三角形の重心位置は底辺から高さh/3のところにある
三角形の面積をAとすると、z軸まわりのモーメントは、平行軸の定理より
$$I_{z'} = I_{z} + A(\frac{h}{3})^2$$
$$\begin{align*}
I_{z}
&= I_{z'} - A(\frac{h}{3})^2 \\
&= \frac{bh^3}{12} - \frac{bh}{2} \cdot \frac{h^2}{9} \\
&= \frac{bh^3}{36}
\end{align*}$$
と、求められました
断面の端までの長さをaとすると、断面係数はZ = I / aで求められるので
のように求められます
表にしてまとめると以下のようになります
| 形状 | 断面二次モーメント | 断面係数 |
 | $$I_{z'} = \frac{bh^3}{12}$$ $$I_{z} = \frac{bh^3}{36}$$ $$e_{1} = \frac{2}{3}h$$ $$e_{2} = \frac{1}{3}h$$ | $$Z_{z'} = \frac{bh^2}{12}$$ $$Z_{{z}_{1}} = \frac{bh^2}{24}$$ $$Z_{{z}_{2}} = \frac{bh^2}{12}$$ |