制御系システムの安定性と極

一次遅れ系の応答でも少し触れましたが、システムの安定性を考えるときには、伝達関数の分母多項式に注目します

この記事では、伝達関数の分母多項式がシステムの安定性にどのような影響を与えるのか、そして「極」について説明していきます

安定性

外乱や目標値の変化によって、振動が生じたときを考えます

時間が経過して、その振動が減衰するならば安定

時間が経過しても振動が続く場合、またはその振動が大きくなっていく(発散する)場合は不安定だと言えます

「最終的に定常値に落ち着いてくれるのなら安定、定常値に落ち着かないなら不安定」とも言い換えられます

このように安定かどうかを判別することを、安定判別と呼びます

安定性は、よくお椀とボールで例えられます

左の図では、ボールを多少移動させてもお椀の底に集まってきますが、お椀をひっくり返すと、ボールは転がり落ちて元の場所には戻りません

制御の目的は、システムを目標の状態に安定させることなので、安定性の判別というのは重要です

特性方程式・根・極・零点

古典制御工学では、システムの安定性を判別するために伝達関数\(G(s)\)に注目します

伝達関数\(G(s)\)は、入力信号のラプラス変換\(U(s)\)と出力信号のラプラス変換\(Y(s)\)の比で表されます

$$G(s) = \frac{Y(s)}{U(s)} = \frac{\beta _{m}s^m + \beta _{m-1}s^{m-1}+ \cdots +\beta _{1}s+\beta _{0}}{s^n + \alpha _{n-1}s^{n-1}+\alpha _{n-2}s^{n-2}+ \cdots +\alpha _{1}s+\alpha _{0}}$$

この伝達関数の「分母多項式=0」とおいた式を特性方程式と呼び、その方程式の根(解)\(p_{1}\cdots p_{n}\)のことを極と呼びます

$$\begin{align*}
s^n + \alpha _{n-1}s^{n-1}+\alpha _{n-2}s^{n-2}+ \cdots +\alpha _{1}s+\alpha _{0} &= 0\\
(s-p_{1})(s-p_{2}) \cdots (s-p_{n}) &= 0
\end{align*}$$

また、「分子多項式=0」の根\(z_{1}\cdots z_{n}\)を零点と呼びます

$$\begin{align*}
\beta _{m}s^m + \beta _{m-1}s^{m-1}+ \cdots +\beta _{1}s+\beta _{0} &= 0\\
(s-z_{1})(s-z_{2}) \cdots (s-z_{n}) &= 0
\end{align*}$$

安定判別を行う上で、極が重要になってきます

安定性と極

システムが安定であるための条件は「伝達関数の全ての極の実部が負である」ことです

一次遅れ系の場合、伝達関数は

$$G(s) = G(s) = \frac{K}{1 + Ts}$$

であるため、システムの極は\(-\frac{1}{T}\)となります

一次遅れ系のインパルス応答とインディシャル応答は

$$\frac{K}{T}e^{-\frac{1}{T}t}~,~K(1-e^{-\frac{1}{T}t})$$

であり、\(e\)のべき指数\(-\frac{1}{T}\)が負になれば、応答が収束することが分かると思います

よって、「伝達関数の全ての極の実部が負であれば収束する」と言えます

また、二次遅れ系の場合、伝達関数は

$$G(s) = \frac{K\omega _{n}^2}{s^2 + 2\zeta \omega _{n}s + \omega _{n}^2}$$

であるため、システムの極は

$$-\zeta \omega _{n}\pm \sqrt{\zeta ^2 -1}\omega _{n}$$

となります

二次遅れ系のインパルス応答とインディシャル応答は(不足減衰)

$$\frac{K\omega _{n}}{\sqrt{1-\zeta ^2}}e^{-\zeta \omega _{n}t}\sin{\sqrt{1-\zeta ^2}\omega _{n}t}~,~K\{1-\frac{1}{\sqrt{1-\zeta ^2}}e^{-\zeta \omega _{n}t}\sin(\sqrt{1-\zeta ^2}\omega _{n}t + \phi)\}$$

であり、\(e\)のべき指数\(-\zeta \omega _{n}\)が負になれば、応答が収束することが分かると思います

よって、同様に「伝達関数の全ての極の実部が負であれば収束する」と言えます

これらを見ると、システムが安定であるための条件は「伝達関数の全ての極の実部が負である」ということがなんとなく納得できたのではないでしょうか

極の表し方

極は、複素平面内に✖マークで表されます

例えば、極の値が\(-3+j~,~-3-j\)であれば、以下のようになります

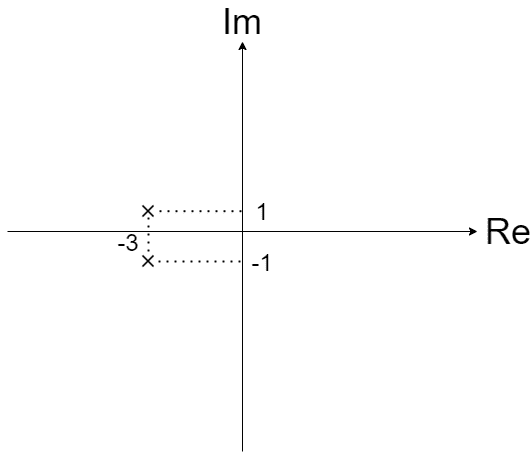
システムが安定であるための条件は「伝達関数の全ての極の実部が負である」ということなので、複素平面にプロットすれば、極が左半面内にあれば安定だと視覚で判断できます

一つでも極が右半面にあれば、そのシステムは不安定だと判断できます

まとめ

最終的に定常値に落ち着いてくれるシステムは安定、定常値に落ち着かないなら不安定である

安定であるかどうかは、伝達関数の「分母多項式=0」とおいた特性方程式の解、つまり極によって決定する

システムが安定であるための条件は「伝達関数の全ての極の実部が負である」

複素平面で表すと、全ての極が左半面に存在していれば安定

古典制御工学まとめに戻る

【参考】
http://www2.kaiyodai.ac.jp/~zhang/Lesson/Seigyo1/seigyo_Eng_6_2008.pdf