この記事では、ラプラス変換、逆ラプラス変換について説明していきます
ラプラス変換とは
ラプラス変換によって、微分・積分が含まれた微分方程式を、簡単な代数方程式に変換することができます
ラプラス変換は、時間領域tの微分方程式を、複素数領域sの代数方程式に変換することで、四則演算で扱うことができるため、計算が容易になるという利点があります
反対に複素数領域sの代数方程式を、時間領域tの微分方程式に変換するのが逆ラプラス変換です
ラプラス変換と逆ラプラス変換の関係は以下の図のようなイメージです
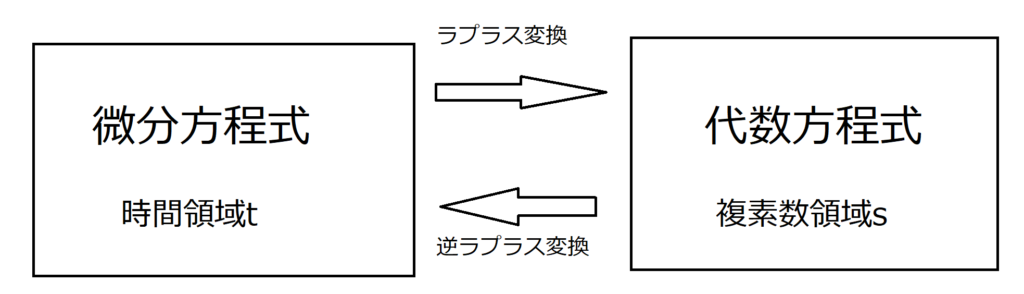
sはラプラス演算子とも言います
ラプラス変換・逆ラプラス変換を使うとどうなるのか
ラプラス変換・逆ラプラス変換を使うと微分方程式を解くのが楽になります
例えば、次のような微分方程式を解くことを考えます
$$\frac{d^2y(t)}{dt^2} + 4\frac{dy(t)}{dt} + 3y(t) = e^{(-t)}~~~(y(0) = 0~,~\frac{dy(0)}{dt} = 0)$$
これをラプラス変換して整理すると(やり方はこの後説明します)、以下のような代数方程式になります
$$s^2 Y(s) + 4sY(s) + 3Y(s) = \frac{1}{s+1}$$
式変形のしやすい形になるので、Y(s)= の形に変形します
$$Y(s) = \frac{1}{(s+1)^2 (s+3)}$$
部分分数分解をして
$$Y(s) = \frac{1}{2(s+1)^2} - \frac{1}{4(s+1)} + \frac{1}{4(s+3)}$$
これを逆ラプラス変換(複素数領域sの代数方程式を、時間領域tの微分方程式に変換)すると
$$y(t) = \frac{te^{-t}}{2} - \frac{e^{-t}}{4} + \frac{e^{-3t}}{4}$$
のように、解が得られました
このように、難しい微分方程式を簡単な代数方程式に変換(ラプラス変換)し、計算を行ってからまた元に戻す(逆ラプラス変換)というやり方をすることによって、簡単な計算をするだけで微分方程式を解くことができます

ラプラス変換・逆ラプラス変換の定義式
実数 t≧0について定義された実数値関数f(t)のラプラス変換は
$$F(s) = \mathcal{L}[f(t)] = \int_{0}^{\infty}f(t)e^{-st}dt$$
で定義される関数F(s)のことです
ここで、sは複素数です
反対に関数F(s)から関数f(t)に戻す逆ラプラス変換はc>0として
f(t)
&= \mathcal{L}^{-1}[F(s)]\\
&= \lim_{p\to\infty}\frac{1}{2pi i}\int_{c-ip}^{c+ip}F(s)e^{st}ds
\end{align*}$$
と定義されています
ちなみに\(\mathcal{L}~ , ~\mathcal{L}^{-1}\)はラプラス変換、逆ラプラス変換の演算子です
ラプラス変換・逆ラプラス変換表
先ほどの定義式から計算する方法もありますが、一般的には以下のラプラス変換表に対応させて計算します
| ラプラス変換前 | ラプラス変換後 |
| 関数$$f(t)$$ | $$\mathcal{L}[f(t)] = F(s)$$ |
| 微分$$\frac{dx(t)}{dt}$$ | $$sX(s) - x(0)$$ |
| 積分$$\int_{0}^{t}x(u)du$$ | $$\frac{1}{s}X(s)$$ |
| $$\frac{d^{n}x(t)}{dt^n}$$ | $$s^{n}X(s) - s^{n-1}x(0) - s^{n-2}x'(0) - … - x^{n-1}(0)$$ |
| デルタ関数$$\delta (t)$$ | $$1$$ |
| $$1$$ | $$\frac{1}{s}$$ |
| $$t$$ | $$\frac{1}{s^2}$$ |
| $$t^n$$ | $$\frac{n!}{s^{n+1}}$$ |
| $$e^{-at}$$ | $$\frac{1}{s+a}$$ |
| $$e^{-at}t^n$$ | $$\frac{n!}{(s+a)^{n+1}}$$ |
| $$\sin{\omega t}$$ | $$\frac{\omega}{s^2+\omega ^2}$$ |
| $$\cos{\omega t}$$ | $$\frac{s}{s^2+\omega ^2}$$ |
| $$e^{-at}\sin{\omega t}$$ | $$\frac{\omega}{(s+a)^2+\omega ^2}$$ |
| $$e^{-at}\cos{\omega t}$$ | $$\frac{s+a}{(s+a)^2+\omega ^2}$$ |
例として、\(e^{-at}\)のラプラス変換が本当に\(\frac{1}{s+a}\)になるのか確認してみましょう
定義に従って
$$\begin{align*}
\mathcal{L}[e^{-at}]
&= \int_{0}^{\infty}e^{-at}e^{-st}dt\\
&= -\frac{1}{s+a}\left[ e^{-(s+a)t} \right]_0^\infty \\
&= -\frac{1}{s+a}(0-1)\\
&= \frac{1}{s+a}
\end{align*}$$
と確認できました
気になる方は他の式も確認してみてください
最初はなかなか変換表を覚えられないと思いますが、問題を解きながら徐々に覚えていけば良いので心配しなくて大丈夫です
微分方程式を解く過程を確認してみる
ラプラス変換・逆ラプラス変換表を使えば、先ほど述べた微分方程式を解くやり方が理解できるはずです
$$\frac{d^2y(t)}{dt^2} + 4\frac{dy(t)}{dt} + 3y(t) = e^{(-t)}~~~(y(0) = 0~,~\frac{dy(0)}{dt} = 0)\dots ①$$
実際にやっていきましょう
まずは、①の微分方程式をラプラス変換します
まず、\(\frac{d^2y(t)}{dt^2}\)は、変換表の上から4つ目を使って
$$\mathcal{L}[\frac{d^2y(t)}{dt^2}] = s^{2}Y(s)-sy(0)-\frac{dy(0)}{dt}$$
のようになります
次に、\(4\frac{dy(t)}{dt}\)は、変換表の上から2つ目を使って
$$\mathcal{L}[4\frac{dy(t)}{dt}] = 4(sY(s)-\frac{dy(0)}{dt})$$
のようになります
さらに、\(y(t)\)は、変換表の一番上を使って
$$\mathcal{L}[3y(t)] = 3Y(s)$$
のようになります
右辺の\(e^{(-t)}\)は、変換表の下から6つ目を使って
$$\mathcal{L}[e^{(-t)}] = \frac{1}{s+1}$$
のようになります
よって、①をラプラス変換すると
$$s^{2}Y(s)-sy(0)-\frac{dy(0)}{dt}(0)+ 4(sY(s)-\frac{dy(0)}{dt}) + 3Y(s) = \frac{1}{s+1}$$
となります
これで式変形をしていきます
初期条件\(y(0) = 0~,~\frac{dy(0)}{dt} = 0\)より
$$s^2 Y(s) + 4sY(s) + 3Y(s) = \frac{1}{s+1}$$
となります
さらに、Y(s) = の形にすると
$$Y(s) = \frac{1}{(s+1)^2(s+3)}\cdots ②$$
のようになります
逆ラプラス変換をしやすいように、②を部分分数分解をします
$$\frac{1}{(s+1)^{2}(s+3)} = \frac{a}{(s+1)^2}+\frac{b}{s+1}+\frac{c}{s+3}$$
整理すると\(a = \frac{1}{2}~,~b=-\frac{1}{4}~,~c=\frac{1}{4}\)が得られるので、②は
$$Y(s) = \frac{1}{2(s+1)^2} - \frac{1}{4(s+1)} + \frac{1}{4(s+3)}\cdots ③$$
のようになります
最後に、③を逆ラプラス変換して、元に戻していきます
\(\frac{1}{2(s+1)^2}\)は、変換表の下から5つ目より
$$\mathcal{L}^{-1}[\frac{1}{2(s+1)^2}] = \frac{te^{-t}}{2}$$
になります
\(\frac{1}{4(s+1)}\)は、変換表の下から6つ目より
$$\mathcal{L}^{-1}[\frac{1}{4(s+1)}] = \frac{e^{-t}}{4}$$
になります
\(\frac{1}{4(s+3)}\)は、変換表の下から5つ目より
$$\mathcal{L}^{-1}[\frac{1}{4(s+3)}] = \frac{e^{-3t}}{4}$$
になります
よって③の逆ラプラス変換は
$$y(t) = \frac{te^{-t}}{2} - \frac{e^{-t}}{4} + \frac{e^{-3t}}{4}$$
のようになり、これが解となります
練習問題
先ほどのラプラス変換表を使って問題を解いてみましょう
(1)~(5)はラプラス変換、(6)~(10)を逆ラプラス変換してください
(1)$$f(t) = e^{-2t}$$
(2)$$f(t) = e^{2t}sin3t$$
(3)
(4)$$f(t) = 2sin3t + cos3t$$
(5)$$te^{2t}$$
(6)$$\frac{2}{s+4}$$
(7)$$\frac{2s+1}{(s+1)(s+2)}$$
(8)$$\frac{2}{s^2+4}$$
(9)$$\frac{2s^2+4s+6}{(s+1)^2(s+3)}$$
(10)$$\frac{4s+5}{s^2+2s+2}$$
【解答】
(1)$$\mathcal{L}[f(t)] = \frac{1}{s+2}$$
(2)$$\mathcal{L}[f(t)] = \frac{3}{(s-2)^2 + 9}$$
(3)
(4)
(5)$$\mathcal{L}[f(t)] = \frac{1}{(s-2)^2}$$
(6)$$\mathcal{L}^{-1}[F(s)] = 2e^{-4t}$$
(7)$$\frac{2s+1}{(s+1)(s+2)} = \frac{a}{s+1} + \frac{b}{s+2}$$とおいてa , bを求めるとa = -1 , b = 3であるから
(8)$$\mathcal{L}^{-1}[F(s)] = sin2t$$
(9)
とおいてa , b , cを求めるとa = 2 , b = -1 , c = 3であるから
(10)
\frac{4s+5}{s^2+2s+2}
&= \frac{4s+5}{(s+1)^2 + 1} \\
&= \frac{4(s+1)+1}{(s+1)^2 + 1} \\
&= \frac{4(s+1)}{(s+1)^2 + 1} + \frac{1}{(s+1)^2 + 1}
\end{align*}$$
より
まとめ
今回はラプラス変換と逆ラプラス変換について説明しました
微分方程式を解くときに非常に便利なものだということは理解できたと思います
最初は変換表に慣れないと思いますが、問題を解いていくとだんだん頭に入っていくので演習が大事です