この記事では、二次遅れ系に対するインパルス応答とインディシャル応答(単位ステップ応答)について解説していきます
二次遅れ要素の伝達関数
制御系のある要素に入力信号を加えたとき、入力信号の位相に対して、出力信号の位相が遅れるような要素を遅れ要素と呼びます
遅れ要素の中でも、伝達関数の分母がsの二次式で表されるものを二次遅れ要素と呼びます
二次遅れ要素の伝達関数は一般に以下のような形で表されます
$$G(s) = \frac{K\omega _{n}^2}{s^2 + 2\zeta \omega _{n}s + \omega _{n}^2}~~~(\zeta > 0~,~\omega _{n} > 0)$$
\(K, \zeta , \omega _{n}\)はそれぞれ、比例ゲイン、減衰率、固有角周波数と呼びます
二次遅れ系のインパルス応答
インパルス入力\(u(t)\)のラプラス変換\(U(s)\)は
$$U(s) = \mathcal{L}[u(t)] = 1$$
であるから、二次遅れ系のインパルス応答\(y(t)\)は
$$y(t) = \mathcal{L}^{-1}[G(s)U(s)] = \mathcal{L}^{-1}[\frac{K\omega _{n}^2}{s^2 + 2\zeta \omega _{n}s + \omega _{n}^2}] $$
となります
二次遅れの伝達関数\(G(s)\)は、そのままの形では逆ラプラス変換できないので、部分分数分解をする必要があります
\(\alpha~,~\beta\)を、伝達関数\(G(s)\)の「分母多項式=0」の解とすると
$$\begin{align*}
s^2 + 2\zeta \omega _{n}s + \omega _{n}^2 &= 0\\
\alpha~,~\beta
&=-\zeta \omega _{n}\pm \sqrt{\zeta ^2 \omega _{n}^2 - \omega ^2}\\
&= -\zeta \omega _{n}\pm \sqrt{\zeta ^2 -1}\omega _{n}\cdots ①
\end{align*}$$
となります
\(\alpha~,~\beta\)は、\(\zeta\)の値によって以下の3つに分類されます
・\(0 < \zeta < 1\)であれば、\(\alpha~,~\beta\)は共役複素数
・\(\zeta = 1\)であれば、\(\alpha=\beta\)の重解
・\(\zeta > 1\)であれば、\(\alpha~,~\beta\)は異なる実数解
よって、それぞれの\(\zeta\)の値について考えます
\(0 < \zeta < 1\)の場合
\(\alpha~,~\beta\)は共役複素数であるから①は
$$\alpha~,~\beta = -\zeta \omega _{n}\pm j\sqrt{1 - \zeta ^2}\omega _{n}$$
となりますので、これを使って部分分数分解をします
\(A,B\)を定数として
$$\begin{align*}
\frac{K\omega _{n}^2}{s^2 + 2\zeta \omega _{n}s + \omega _{n}^2}&= \frac{K\omega_ {n}^2}{(s-\alpha)(s-\beta)} = \frac{A}{s-\alpha} + \frac{B}{s-\beta}\\
K\omega _{n}^2 &= A(s-\beta)+B(s-\alpha)\\
&= (A+B)s - (A\beta + B\alpha)\\
&= (A+B)s - \{-\zeta \omega _{n}(A+B)-Aj\sqrt{1 - \zeta ^2 }\omega _{n} + Bj\sqrt{1 - \zeta ^2}\omega _{n}\}\\
\end{align*}$$
これが恒等式となるから、係数を比較してみると
$$\begin{align*}
A+B&=0\\
K\omega _{n}^2 &= - \{-\zeta \omega _{n}(A+B)-Aj\sqrt{1 - \zeta ^2 }\omega _{n} + Bj\sqrt{1 - \zeta ^2}\omega _{n}\}\\
\end{align*}$$
整理すると、\(A~,~B\)はそれぞれ
$$A=\frac{K\omega _{n}}{2j\sqrt{1- \zeta ^2}}~,~B=-\frac{K\omega _{n}}{2j\sqrt{1- \zeta ^2}}$$
となります
\(A,B\)を代入すると
$$\frac{K\omega _{n}^2}{s^2 + 2\zeta\omega _{n}s + \omega _{n}^2} = \frac{K\omega _{n}}{2j\sqrt{1-\zeta ^2}}(\frac{1}{s-\alpha}-\frac{1}{s-\beta})$$
となるから、インパルス応答\(y(t)\)は
$$\begin{align*}
y(t)
&= \mathcal{L}^{-1}[U(s)G(s)]\\
&= \mathcal{L}^{-1}[\frac{K\omega _{n}}{2j\sqrt{1-\zeta ^2}}(\frac{1}{s-\alpha}-\frac{1}{s-\beta})]\\
&= \frac{K\omega _{n}}{2j\sqrt{1-\zeta ^2}}(e^{\alpha t} - e^{\beta t})\\
&= \frac{K\omega _{n}}{2j\sqrt{1-\zeta ^2}}\{e^{(-\zeta \omega _{n}+j\sqrt{1-\zeta ^2})t}-e^{(-\zeta \omega _{n}-j\sqrt{1-\zeta ^2})t}\}\\
&= \frac{K\omega _{n}}{2j\sqrt{1-\zeta ^2}}e^{-\zeta \omega _{n}t}\{e^{j\sqrt{1-\zeta ^2}\omega _{n} t} - e^{-j\sqrt{1-\zeta ^2}\omega _{n} t}\}\\
&オイラーの公式e^{jt} = \cos t + j\sin tより\\
&= \frac{K\omega _{n}}{2j\sqrt{1-\zeta ^2}}e^{-\zeta \omega _{n}t}\{\cos{\sqrt{1-\zeta ^2}\omega _{n}t} + j\sin{\sqrt{1-\zeta ^2}\omega _{n}t}-\cos{\sqrt{1-\zeta ^2}\omega _{n}t} + j\sin{\sqrt{1-\zeta ^2}\omega _{n}t}\}\\
&= \frac{K\omega _{n}}{\sqrt{1-\zeta ^2}}e^{-\zeta \omega _{n}t}\sin{\sqrt{1-\zeta ^2}\omega _{n}t}
\end{align*}$$
となります
\(\zeta = 0\)の場合
\(\alpha,\beta\)は、\(\alpha,\beta = -\omega _{n}\)の重解となりますので、伝達関数は
$$G(s) = \frac{K\omega _{n}^2}{s^2 + 2\zeta \omega _{n} + \omega _{n}^2} = \frac{K\omega _{n}^2}{(s+\omega _{n})^2}$$
となります
インパルス応答\(y(t)\)は
$$\begin{align*}
y(t)
&= \mathcal{L}^{-1}[U(s)G(s)]\\
&= \mathcal{L}^{-1}[\frac{K\omega _{n}^2}{(s+\omega _{n})^2}]\\
&= K\omega _{n}^2 te^{-\omega _{n}t}
\end{align*}$$
となります
\(\zeta > 1\)の場合
\(\alpha,\beta\)は、異なる2つの実数解となるため①は
$$\alpha,\beta = -\zeta \omega _{n}\pm \sqrt{\zeta ^2 -1}\omega _{n}$$
となります
\(A,B\)を定数として、同じように部分分数分解を進めていきます
$$\begin{align*}
\frac{K\omega _{n}}{s^2 + 2\zeta \omega _{n}s + \omega _{n}^2} &= \frac{A}{s-\alpha} + \frac{B}{s-\beta}\\
K\omega _{n}^2 = (A+B)s - (A\beta + B\alpha)
\end{align*}$$
これが恒等式となるから、係数を比較してみると
$$\begin{align*}
A+B &= 0\\
K\omega _{n}^2 = 2A\sqrt{\zeta ^2 -1}\omega _{n}
\end{align*}$$
整理すると、\(A~,~B\)はそれぞれ
$$A=\frac{K\omega _{n}}{2\sqrt{\zeta ^2 - 1}}~,~B=-\frac{K\omega _{n}}{2\sqrt{\zeta ^2 - 1}}$$
となります
\(A,B\)を代入すると
$$\frac{K\omega _{n}^2}{s^2 + 2\zeta \omega _{n}s + \omega _{n}^2} = \frac{K\omega _{n}}{2\sqrt{\zeta ^2 - 1}}(\frac{1}{s-\alpha}-\frac{1}{s-\beta})$$
となるから、インパルス応答\(y(t)\)は
$$\begin{align*}
y(t)
&= \mathcal{L}^{-1}[G(s)U(s)]\\
&= \mathcal{L}^{-1}[\frac{K\omega _{n}}{2\sqrt{\zeta ^2 - 1}}(\frac{1}{s-\alpha}-\frac{1}{s-\beta})]\\
&= \frac{K\omega _{n}}{2\sqrt{\zeta ^2 - 1}}\{e^{(-\zeta \omega _{n}+\sqrt{\zeta ^2 -1}\omega _{n})t} - e^{(-\zeta \omega _{n}-\sqrt{\zeta ^2 -1}\omega _{n})t}\}
\end{align*}$$
インパルス応答のグラフ
分類した3つの全てで、初期値\(y(0) = 0\)と最終値\(\lim_{t \to \infty}y(t) = 0\)であることが分かります
それぞれのグラフを書いてみて、二次遅れ系のパラメータ\(\zeta~,~\omega _{n}\)がグラフにどのような影響を与えるかについて考察します
\(0 < \zeta < 1\)の場合
\(0 < \zeta < 1\)のときのインパルス応答は、振動しながら徐々に0に向かって収束していきます
これは、不足減衰と呼ばれています
\(K=1~,~\omega _{n}=1\)として、\(\zeta\)の値を変更してみると

\(\zeta\)が大きくなるほど、より早く0に収束することが分かります
今度は、\(K=1~,~\zeta = 0.5\)として、\(\omega _{n}\)の値を変更してみると
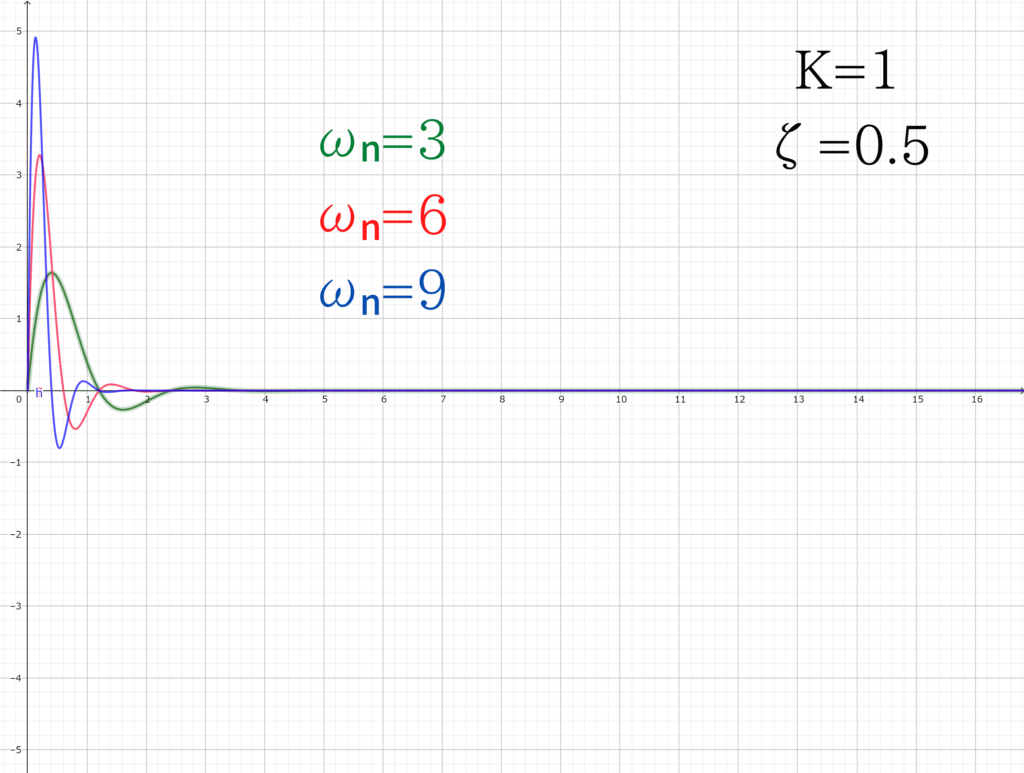
\(\omega _{n}\)が大きくなるほど、振幅は大きくなりますが、より早く0に収束することが分かります
\(\zeta = 1\)の場合
\(\zeta = 1\)のときのインパルス応答は、sinやcos関数が存在しないため、振動しません
\(\zeta = 1\)は、振動するかどうかの境目であり、臨界減衰と呼ばれています
インパルス入力の方向に一度だけ振れ、その後0に向かって収束していきます
\(K=1\)として、\(\zeta\)の値を変更してみると
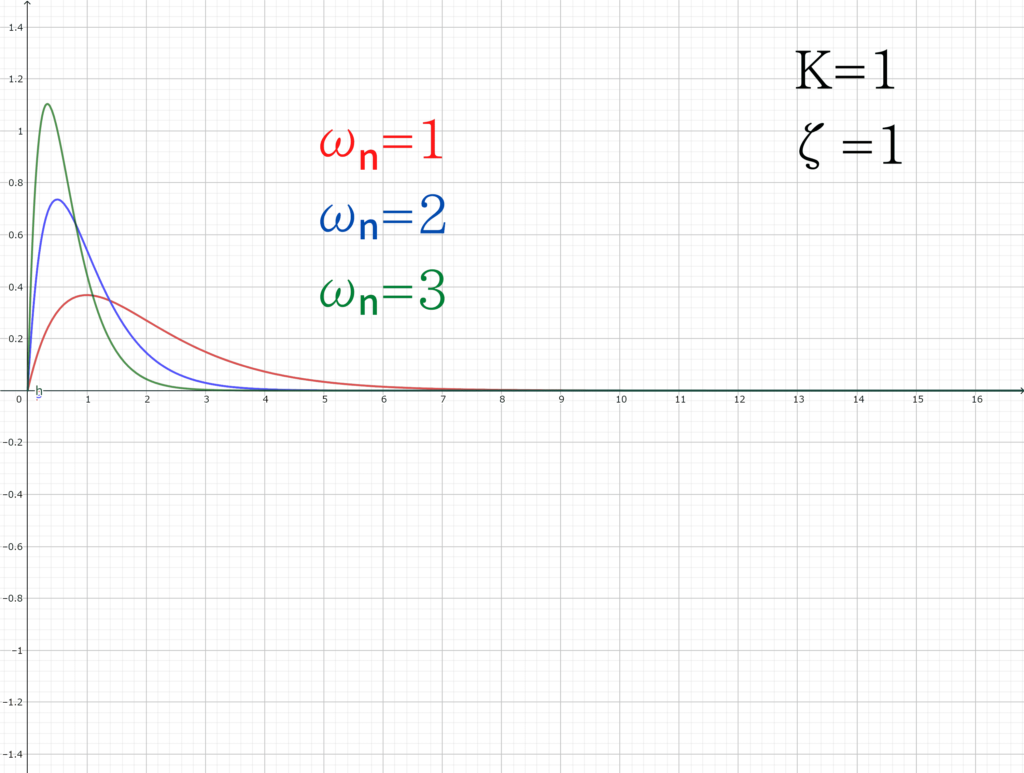
\(\omega _{n}\)が大きくなるほど、振幅は大きくなりますが、より早く0に収束することが分かります
\(\zeta > 1\)の場合
\(\zeta > 1\)のときのインパルス応答は、sinやcos関数が存在しないため、振動しません
これは、過減衰と呼ばれています
\(K=1~,~\omega _{n}=1\)として、\(\zeta\)の値を変更してみると
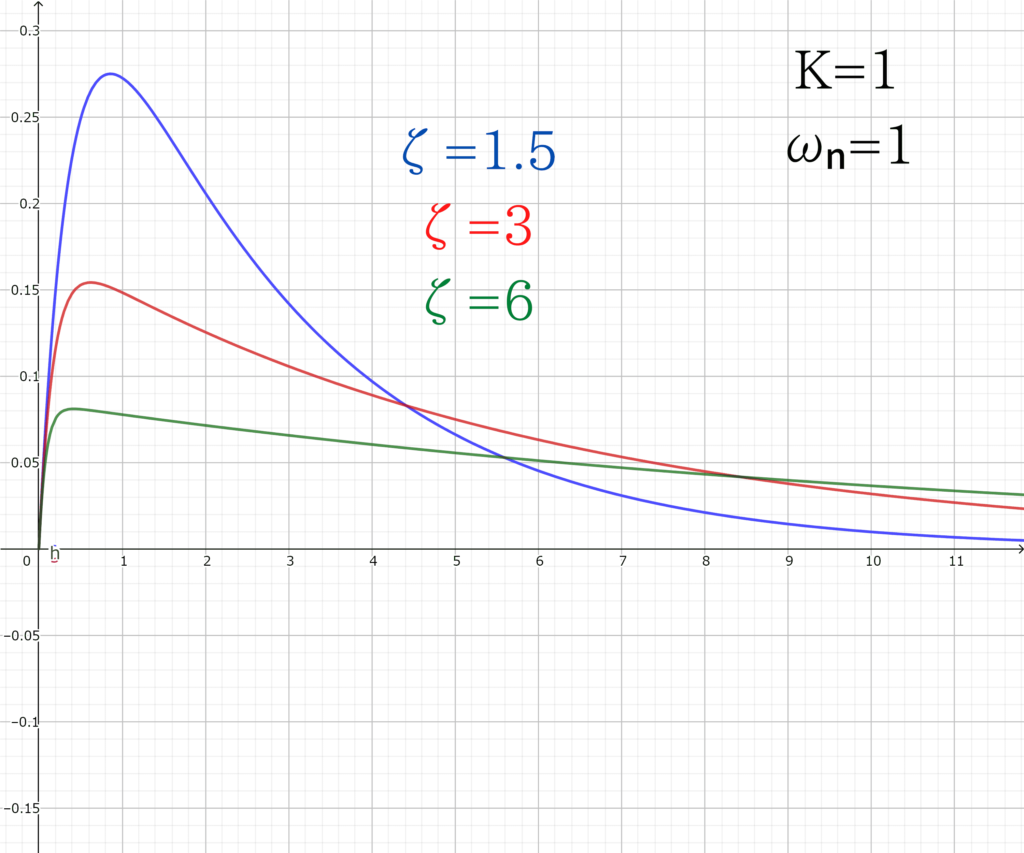
\(\zeta\)が大きくなるほど、振幅は大きくなりますが、0に収束するまでの時間が多くなります
\(K=1~,~\zeta=2\)として、\(\zeta\)の値を変更してみると

\(\omega _{n}\)が大きくなるほど、振幅は大きくなりますが、より早く0に収束することが分かります
二次遅れ系のインディシャル応答
単位ステップ入力\(u(t)\)のラプラス変換\(U(s)\)は
$$U(s) = \mathcal{L}[u(t)] = \frac{1}{s}$$
であるから、二次遅れ系のインディシャル応答\(y(t)\)は
$$y(t) = \mathcal{L}^{-1}[G(s)U(s)] = \mathcal{L}^{-1}[\frac{K\omega _{n}^2}{s(s^2 + 2\zeta \omega _{n}s + \omega _{n}^2)}] $$
となります
\(\frac{K\omega _{n}^2}{s(s^2 + 2\zeta \omega _{n}s + \omega _{n}^2)}\)は、そのままの形では逆ラプラス変換できないので、部分分数分解をする必要があります
\(A,B,C\)を定数として、\(\alpha~,~\beta\)を①と同様とすると、以下のように部分分数分解を行います
$$\frac{K\omega _{n}^2}{s(s^2 + 2\zeta \omega _{n}s + \omega _{n}^2)} = \frac{A}{s} + \frac{B}{s-\alpha} + \frac{C}{s-\beta}\cdots ②$$
②を逆ラプラス変換すると、インディシャル応答\(y(t)\)が求められます
$$\begin{align*}
y(t)
&= \mathcal{L}^{-1}[\frac{K\omega _{n}^2}{s(s^2 + 2\zeta \omega _{n}s + \omega _{n}^2)}] \\
&= \mathcal{L}^{-1}[\frac{A}{s} + \frac{B}{s-\alpha} + \frac{C}{s-\beta}] \\
&= A + Be^{\alpha t} + Ce^{\beta t}\cdots ③
\end{align*}$$
インパルス応答と同様に、\(\zeta\)の値によって場合分けして考えます
\(0 < \zeta < 1\)の場合(不足減衰)
\(\alpha~,~\beta\)は共役複素数であるから①は
$$\alpha~,~\beta = -\zeta \omega _{n}\pm j\sqrt{1 - \zeta ^2}\omega _{n}$$
であり、②を整理していくと\(A,B,C\)が求められます
$$A=K~,~B=-K\frac{\zeta + j\sqrt{1-\zeta ^2}}{j2\sqrt{1-\zeta ^2}}~,~C=K\frac{\zeta - j\sqrt{1 - \zeta ^2}}{j2\sqrt{1-\zeta ^2}}\cdots ④$$
④を③に代入して整理すると、インディシャル応答\(y(t)\)は
$$y(t) = K\{1-\frac{1}{\sqrt{1-\zeta ^2}}e^{-\zeta \omega _{n}t}\sin(\sqrt{1-\zeta ^2}\omega _{n}t + \phi)\}$$
となります、ただし
$$~\phi = \tan ^{-1}\frac{\sqrt{1-\zeta ^2}}{\zeta}$$
\(\zeta = 1\)の場合(臨界減衰)
\(\alpha,\beta\)は、\(\alpha,\beta = -\omega _{n}\)の重解となりますので、部分分数分解すると
$$\frac{K\omega _{n}^2}{s(s^2 + 2\zeta \omega _{n}s + \omega _{n}^2)} = \frac{K\omega _{n}^2}{s(s+\omega _{n})^2} = K\{\frac{1}{s}-\frac{1}{s+\omega _{n}} - \frac{\omega _{n}}{(s+\omega _{n})^2}\}$$
のようになります
よって、インディシャル応答\(y(t)\)は
$$\begin{align*}
y(t)
&= \mathcal{L}^{-1}[\frac{K\omega _{n}^2}{s(s^2 + 2\zeta \omega _{n}s + \omega _{n}^2)}]\\
&= \mathcal{L}^{-1}[\frac{K\omega _{n}^2}{s(s+\omega _{n})^2}]\\
&= \mathcal{L}^{-1}[K\{\frac{1}{s}-\frac{1}{s+\omega _{n}} - \frac{\omega _{n}}{(s+\omega _{n})^2}\}]\\
&= K\{1-e^{-\omega _{n}t}(1+\omega _{n}t)\}
\end{align*}$$
となります
\(\zeta > 1\)の場合(過減衰)
\(\alpha,\beta\)は、異なる2つの実数解となるため①は
$$\alpha,\beta = -\zeta \omega _{n}\pm \sqrt{\zeta ^2 -1}\omega _{n}$$
であり、②を整理していくと\(A,B,C\)が求められます
$$A=K~,~B=-K\frac{\zeta + \sqrt{1-\zeta ^2}}{2\sqrt{1-\zeta ^2}}~,~C=K\frac{\zeta - \sqrt{1 - \zeta ^2}}{2\sqrt{1-\zeta ^2}}\cdots ⑤$$
⑤を③に代入して整理すると、インディシャル応答\(y(t)\)は
$$y(t) = K\{1 - \frac{\zeta + \sqrt{1-\zeta ^2}}{2\sqrt{1-\zeta ^2}}e^{(-\zeta \omega _{n}+\sqrt{\zeta ^2 -1}\omega _{n})t} + \frac{\zeta - \sqrt{1-\zeta ^2}}{2\sqrt{1-\zeta ^2}}e^{(-\zeta \omega _{n}-\sqrt{\zeta ^2 -1}\omega _{n})t}\}$$
となります
インディシャル応答のグラフ
分類した3つの全てで、初期値\(y(0) = 0\)と最終値\(\lim_{t \to \infty}y(t) = K\)であることが分かります
それぞれのグラフを書いてみて、二次遅れ系のパラメータ\(\zeta~,~\omega _{n}\)がグラフにどのような影響を与えるかについて考察します
\(0 < \zeta < 1\)の場合(不足減衰)
\(0 < \zeta < 1\)のときのインディシャル応答は、振動しながら徐々に定常値\(K\)に向かって収束していきます
また、オーバーシュートも存在します
\(K=1~,~\omega _{n}=1\)として、\(\zeta\)の値を変更してみると

\(\zeta\)が大きくなるほど、オーバーシュートも大きくなり、収束するまでの時間が多く必要になることが分かります
\(K=1~,~\zeta=0.3\)として、\(\\omega _{n}\)の値を変更してみると
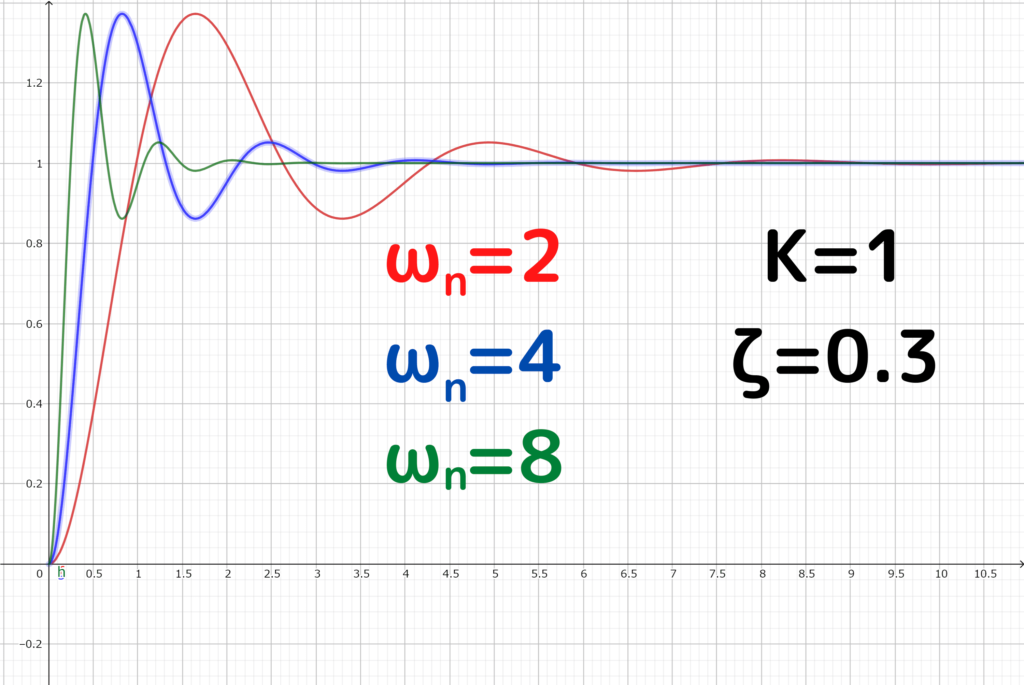
\(\omega _{n}\)を大きくしても、オーバーシュートは変わりませんが、収束するまでの時間が短くなっています
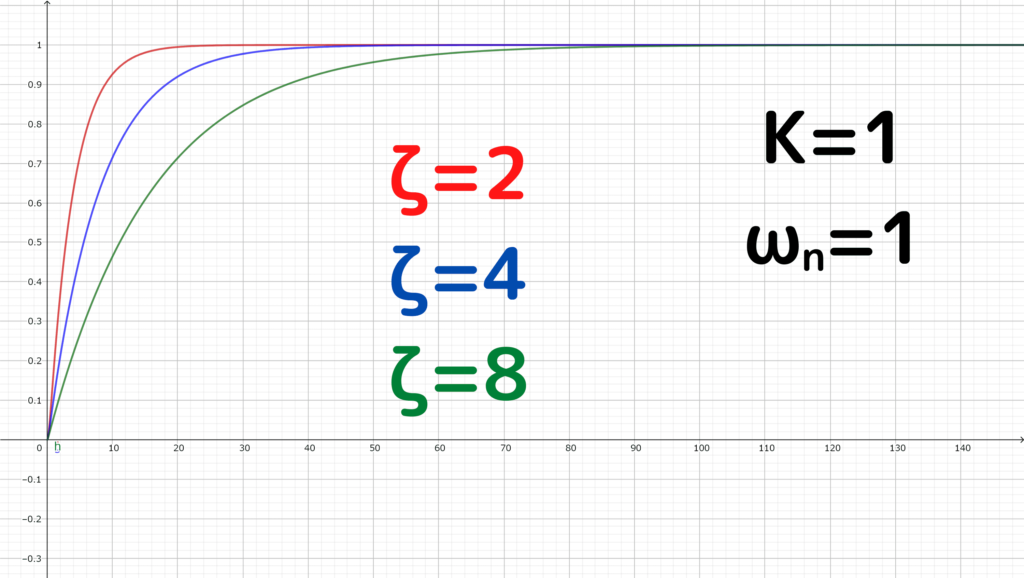
\(\zeta = 1\)の場合(臨界減衰)
インパルス応答と同様に、sinやcos関数が存在しないため、振動しません
\(K=1\)として、\(\omega _{n}\)の値を変更してみると
\(\omega _{n}\)が大きくなるほど、収束するまでの時間が短くなっています
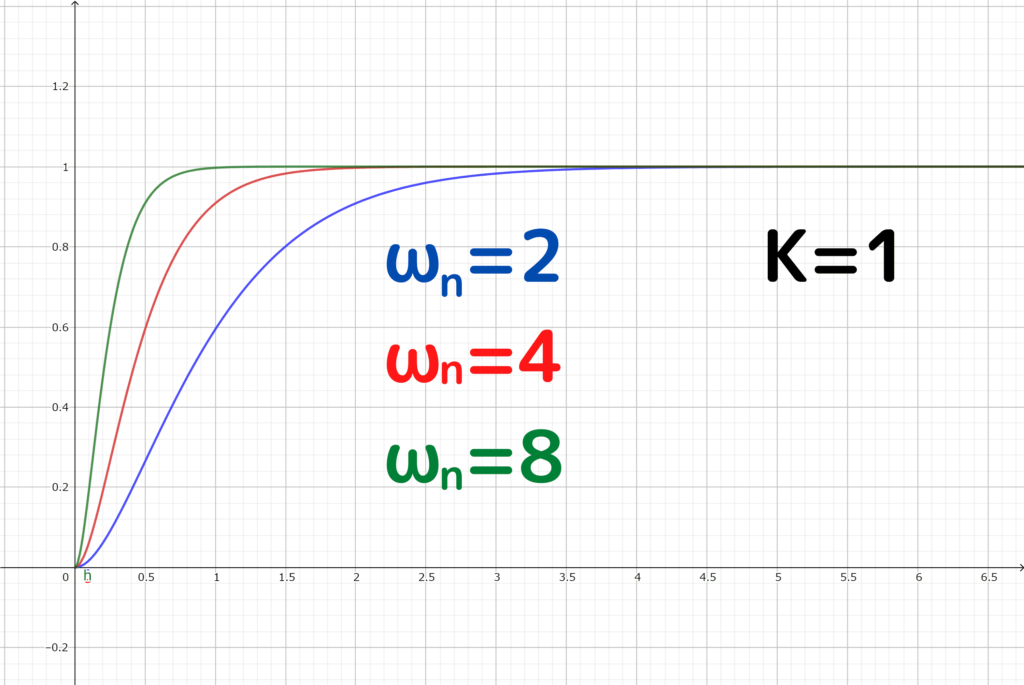
\(\zeta > 1\)の場合(過減衰)
インパルス応答と同様に、sinやcos関数が存在しないため、振動しません
\(K=1~,~\omega _{n}=1\)として、\(\zeta\)の値を変更してみると
\(\zeta\)が大きくなるほど、収束するまでの時間が多く必要になることが分かります
\(K=1~,~\zeta=2\)として、\(\\omega _{n}\)の値を変更してみると
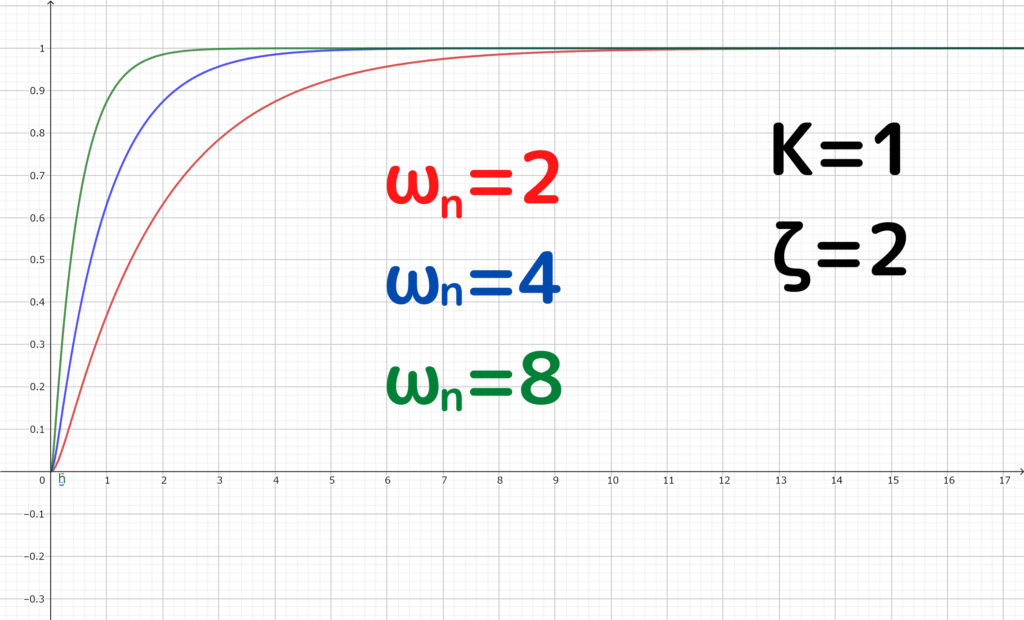
\(\omega _{n}\)が大きくなるほど、収束するまでの時間が短くなっています
まとめ
この記事の内容を簡単にまとめておきます
二次遅れ要素の伝達関数\(G(s)\)
$$G(s) = \frac{K\omega _{n}^2}{s^2 + 2\zeta \omega _{n}s + \omega _{n}^2}$$
不足減衰のときの応答
インパルス応答
$$\frac{K\omega _{n}}{\sqrt{1-\zeta ^2}}e^{-\zeta \omega _{n}t}\sin{\sqrt{1-\zeta ^2}\omega _{n}t}$$
インディシャル応答
$$K\{1-\frac{1}{\sqrt{1-\zeta ^2}}e^{-\zeta \omega _{n}t}\sin(\sqrt{1-\zeta ^2}\omega _{n}t + \phi)\}$$
ただし
$$\phi = \tan ^{-1}\frac{\sqrt{1-\zeta ^2}}{\zeta}$$
臨界減衰のときの応答
インパルス応答
$$K\omega _{n}^2 te^{-\omega _{n}t}$$
インディシャル応答
$$K\{1-e^{-\omega _{n}t}(1+\omega _{n}t)\}$$
過減衰のときの応答
インパルス応答
$$\frac{K\omega _{n}}{2\sqrt{\zeta ^2 - 1}}\{e^{(-\zeta \omega _{n}+\sqrt{\zeta ^2 -1}\omega _{n})t} - e^{(-\zeta \omega _{n}-\sqrt{\zeta ^2 -1}\omega _{n})t}\}$$
インディシャル応答
$$K\{1 - \frac{\zeta + \sqrt{1-\zeta ^2}}{2\sqrt{1-\zeta ^2}}e^{(-\zeta \omega _{n}+\sqrt{\zeta ^2 -1}\omega _{n})t} + \frac{\zeta - \sqrt{1-\zeta ^2}}{2\sqrt{1-\zeta ^2}}e^{(-\zeta \omega _{n}-\sqrt{\zeta ^2 -1}\omega _{n})t}\}$$
初期値と定常値
インパルス応答
$$y(0) = 0~,~\lim_{t \to \infty}y(t) = 0$$
インディシャル応答
$$y(0) = 0~,~\lim_{t \to \infty}y(t) = K$$