今回は1×1、2×2、3×3の行列式の求め方について解説します。
4×4の行列式についてはこちらの記事で解説します。
1×1の行列式
1×1の行列の要素がそのまま行列式となります。
例えば行列Aが$$A = [3]$$の場合、行列式は$$|A| = 3$$となります。
このように一般に行列Aの逆行列は|A|のように記述します。
2×2の行列式
次のような2×2の行列Aがあったとします。$$A = \left[\begin{array}{rr} a & b \\ c & d\end{array} \right]$$この行列Aの行列式は$$|A| = ad - bc$$となります。
3×3の行列式
次のような3×3の行列Aがあったとします。$$A = \left[\begin{array}{rrr} a & b & c\\ d & e & f \\ g & h & i\end{array} \right]$$
ここで行列式を求めるために登場するのが「サラスの規則」です。
サラスの規則は「左上から右下に向かってかけて足したもの」ー「右上から左下に向かってかけて足したもの」というものです。言葉だけではわかりにくいと思いますので図で示すと
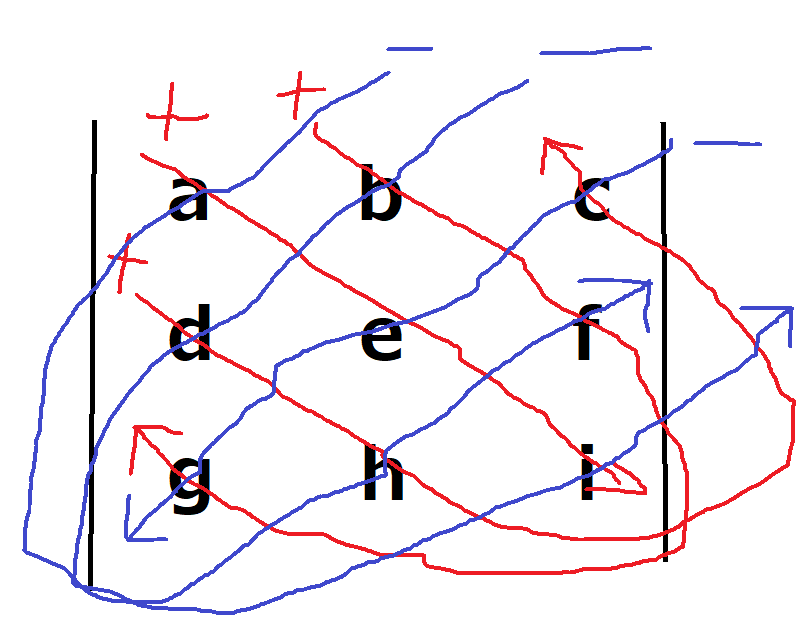
このような感じになります。
サラスの規則よりこの行列Aの行列式は
となります。
2×2のときもサラスの規則が使えることがわかると思います。
ちなみに4×4以上の行列ではサラスの規則が使えないので注意して下さい。
それでは練習問題で演習してみましょう。
練習問題
(1)次の行列Aの行列式を求めよ。$$A = \left[\begin{array}{rr} 1 & 2 \\ 1 & 3\end{array} \right]$$
(2)次の行列Bの行列式を求めよ。$$B = \left[\begin{array}{rrr} 1 & 2 & 0\\ 1 & 1 & 2 \\ 2 & 1 & 1\end{array} \right]$$
(3)次の行列Cの行列式を求めよ。$$C = \left[\begin{array}{rrr} 1 & 2 & 0\\ 1 & 1 & 2 \\ 2 & 1 & 1\end{array} \right]$$
【解答】
(1)Aの行列式|A|はサラスの公式より$$|A| = 1*3 -1*2 = 1$$となります。
(2)Bの行列式|B|はサラスの公式より
となります。
(3)Cの行列式|C|はサラスの公式より
となります。
まとめ
今回は1×1、2×2、3×3の行列式の求め方について解説しました。
行列式の求め方は基本的な内容なので理解できるようにしましょう。
また、今回紹介したサラスの規則は4×4以上の行列では使えないので注意して下さい。